3.4: 多缝干扰
- Page ID
- 202423
在本节结束时,您将能够:
- 描述多缝干扰的次要最大值的位置和强度
分析光线穿过两个狭缝的干扰确定了干扰的理论框架,并让我们对托马斯·杨的实验有了历史见解。 但是,现代狭缝干扰的许多应用不仅使用两个狭缝,还使用许多狭缝,出于实际目的接近无穷大。 关键光学元件被称为衍射光栅,这是光学分析中的重要工具,我们在衍射一章中对此进行了详细讨论。 在这里,我们开始分析多缝干扰,方法是从对双狭缝 (N=2) 的分析结果中提取出来,并将其扩展到具有三个、四个以及更多狭缝数量的配置。
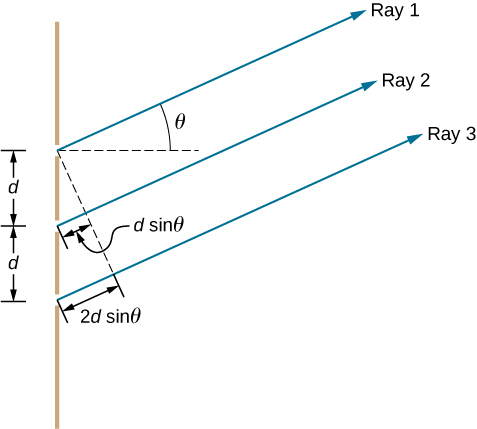
图中\(\PageIndex{1}\)显示了最简单的多缝干扰案例,有三个狭缝,即 N=3。 狭缝之间的间距为 d,相邻狭缝之间的路径长度差为 d sin β,与双狭缝的情况相同。 新增的是,第一个和第三个狭缝的路径长度差为 2d sin β。 建设性干扰的条件与双缝的条件相同,也就是说
\[d \sin θ=mλ \nonumber \]
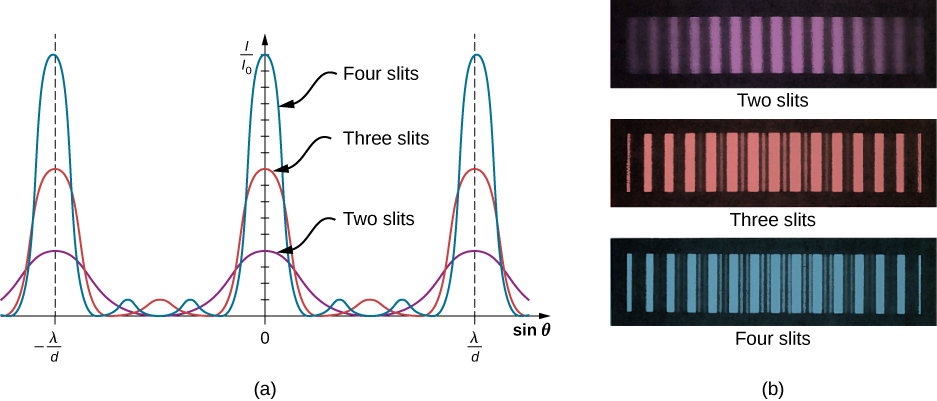
当满足这个条件时,2d sin β 自动成为 λ的倍数,因此所有三条射线都建设性地结合在一起,此处出现的明亮条纹称为主最大值。 但是,当相邻狭缝之间的路径长度差仅为 λ/2 时会发生什么? 我们可以认为第一和第二条射线具有破坏性干扰,但第三条射线保持不变。 我们看到的不是像双缝那样获得深色条纹或最小值,而是看到强度低于主最大值的次要最大值。
通常,对于 N 个狭缝,只要存在未成对的射线,并且由于破坏性干扰而没有消失,就会出现这些次要最大值。 这发生在主最大值之间间隔均匀的 (N−2) 位置。 在主最大值时,电磁波的振幅相应地减小到波浪的1/N,而与波浪振幅的平方成正比的光强度减小到\(1/N^2\)与主最大值相比的强度。 如图 2、3 和 4 个狭缝的\(\PageIndex{2}\)干扰条纹图案。 随着狭缝数量的增加,会出现更多的次要最大值,但主最大值显示,每个最大值(主最大值或次要最大值)之间都有一条暗条纹。 随着 N 的增大以及明暗条纹数量的增加,由于相邻的暗条纹位置较近,最大值的宽度会变窄。 由于光能的总量保持不变,因此较窄的最大值要求每个最大值达到相应的更高强度。