3.2: Young 的双缝干扰

Last updated
Save as PDF

Page ID: 202486

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

在本节结束时，您将能够：

解释干扰现象
定义双缝的构造干扰和破坏性干扰

荷兰物理学家克里斯蒂安 ·惠更斯（1629—1695 年）认为光是波浪，但艾萨克·牛顿没有。牛顿认为，对于颜色以及当时可以观察到的干扰和衍射效应，还有其他解释。由于牛顿的巨大声誉，他的观点普遍占了上风；惠更斯原理奏效的事实不被视为证明光是波浪的直接证据。许多年后的1801年，英国物理学家兼医生托马斯· 杨（Thomas Young）（1773—1829 年）用他现在经典的双缝实验展示了光学干扰，人们开始接受光的波浪特征。

如果不是一个而是两个波浪源，则可能会使海浪产生干扰，就像水上的波浪一样（图\(\PageIndex{1}\)）。如果光是电磁波，则在适当情况下它必须表现出干扰效应。在杨的实验中，阳光穿过木板上的针孔。新出现的光束落在第二块板上的两个针孔上。然后，两个针孔发出的光线落在屏幕上，在屏幕上观察到明暗的斑点图案。这种模式被称为条纹，只能通过干扰（一种波浪现象）来解释。

图中显示了干涉图案的照片。蓝色表面上可见的白色圆圈的波浪从两个中心发出，并在多个点处相交。 — 图\(\PageIndex{1}\)：波纹水箱中的圆形水波产生的干扰图案的照片。两个细柱塞在水面上下相位振动。圆形水浪由每个柱塞产生并发出。

我们可以借助 Figure 来分析双缝干扰\(\PageIndex{2}\)，它描绘了一个类似于 Young 的设备。来自单色光源的光落在狭缝上\(S_0\)。发出的光线入射到\(S_0\)另外两个狭缝上\(S_2\)，这两个缝隙\(S_1\)与之等距\(S_0\)。然后，和发出的光会产生屏幕上的干扰条纹图案\(S_2\)。\(S_1\) 假设所有狭缝都非常狭窄，可以将其视为惠根斯小波（光的本质）的次要点源。 Sl\(S_1\) it\(S_2\) s an d 相距 d (\(d≤1\,mm\))，屏幕和缝隙之间的距离为 D（约 1m），远大于 d。

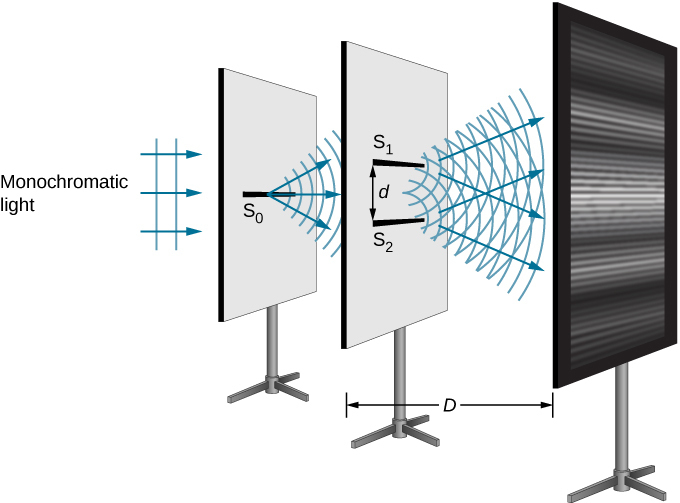
图为双缝实验的示意图。单色光首先穿过狭窄的狭缝 S0。接下来是穿过两个狭缝 S1 和 S2，其中一个缝隙位于另一个之上，由距离 d 隔开。最后，光线到达形成干扰图案的屏幕。双缝屏幕和最终屏幕之间的距离为 D。 — 图\(\PageIndex{2}\)：使用单色光和窄缝的双缝干涉实验。屏幕上可以观察到干扰惠更斯\(S_1\)小波产生的条纹。\(S_2\)

由于假定\(S_0\)是单色光的点源，因此次要惠更斯小波离开\(S_1\)并\(S_2\)始终保持恒定的相位差（在本例中为零，因为\(S_1\)和\(S_2\)等距\(S_0\)）并且相位差相同频率。据说消息来源\(S_1\)\(S_2\)是连贯的。我们所说的相干波是指波相位或具有明确的相位关系。 “不相干” 一词意味着波浪具有随机的相位关系，如果\(S_1\)和\(S_2\)由两个独立的光源而不是单个光源照亮，则会出现这种关系\(S_0\)。两个独立的光源（可能是同一盏灯或太阳中的两个独立区域）通常不会一致发光，也就是说，不连贯地发光。另外，由于\(S_1\)和距离\(S_2\)的距离相同\(S_0\)，两个惠更斯小波的振幅是相等的。

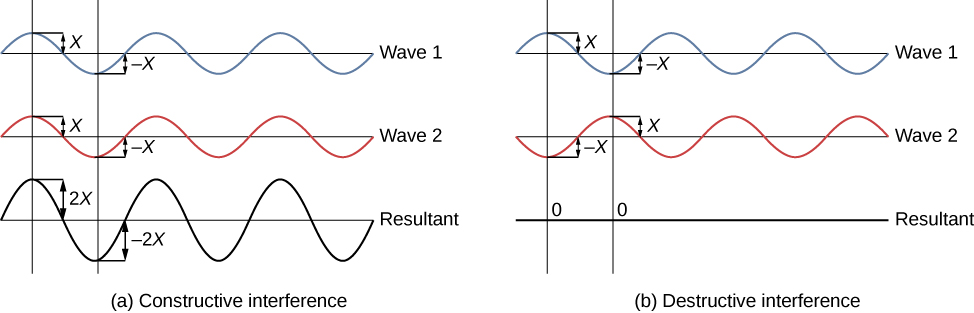
Young 使用阳光，其中每个波长形成自己的图案，这使得效果更难看清。在接下来的讨论中，我们举例说明了使用单色光（单 λ）进行的双缝实验，以阐明效果。图中\(\PageIndex{3}\)显示了具有相同波长和振幅的两波的纯粹构造性和破坏性干扰。

左图是建设性干扰的示意图。两个相同的波相位产生振幅翻倍的波浪。右图是破坏性干扰的示意图。两个相同的波相位偏移了半个波长，从而产生了振幅为零的波浪。 — 图\(\PageIndex{3}\)：波浪的振幅相加。 (a) 当相同的波相位时，会获得纯粹的构造干扰。 (b) 当相同的波完全异相或偏移半个波长时，就会发生纯破坏性干扰。

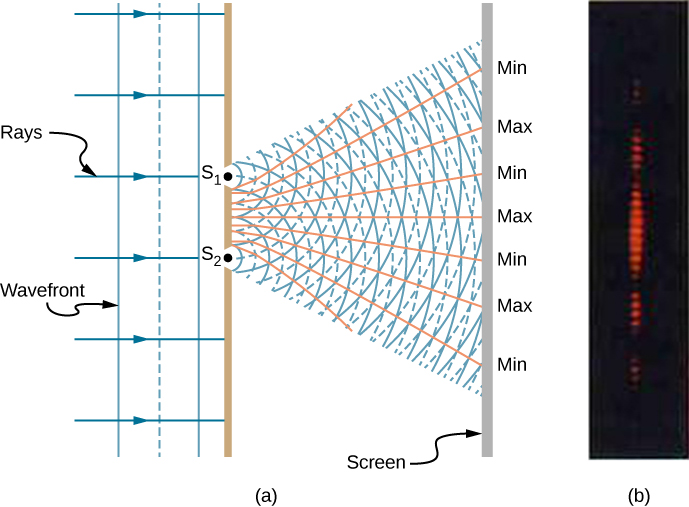
当光线穿过狭窄的狭缝时，狭缝充当相干波的来源，光线以半圆波的形式扩散，如图所示\(\PageIndex{1a}\)。纯粹的建设性干扰发生在波峰到波峰或波谷到低谷的地方。纯粹的破坏性干扰发生在波峰到低谷的地方。光线必须落在屏幕上并散射到我们的眼睛中，我们才能看到图案。水浪的类似模式如图所示\(\PageIndex{1}\)。请注意，具有建设性和破坏性干扰的区域以明确的角度从狭缝向外移动，直至原始光束。这些角度取决于波长和狭缝之间的距离，如下所示。

左图是双缝实验的示意图。单色光进入两个狭缝 S1 和 S2。光线穿过狭缝后会散开，波浪建设性和破坏性地重叠。右图是条纹图案的照片，显示亮点以线条对齐。 — 图\(\PageIndex{4}\)：双狭缝产生两个干扰的相干波源。 (a) 光线从每个狭缝向外扩散（衍射），因为狭缝很窄。这些波浪重叠和干扰具有建设性（亮线）和破坏性（暗区）。只有当光线落在屏幕上并散射到我们的眼睛里时，我们才能看到这一点。 (b) 当穿过双缝隙的光线落在屏幕上时，我们会看到这样的图案。

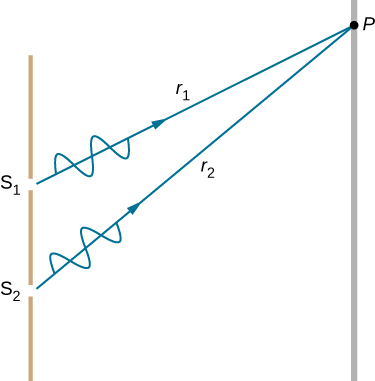
要了解双缝干扰模式，请考虑两个波浪如何从狭缝传播到屏幕（图\(\PageIndex{5}\)）。每个缝隙与屏幕上给定点的距离都不同。因此，不同数量的波长适合每条路径。波浪从相位狭缝（波峰到波峰）开始，但如果路径的长度相差半个波长，它们最终可能会在屏幕上异相（波峰到波谷），从而造成破坏性干扰。如果路径相差整个波长，则波浪相位（波峰到波峰）到达屏幕，产生建设性的干扰。更一般地说，如果两个波长\(\Delta l\)之间的路径长度差异是波长的任意半整数 [(1/2) l、(3/2) λ等]，则会发生破坏性干扰。同样，如果路径长度差异是波长的任意整数数（α、2λ、3λ等），则会发生构造干扰。这些条件可以表示为方程式：

\[\underbrace{\Delta l = m \lambda}_{\text{constructive interference}} \nonumber \]

为了\(m = 0, \, ±1, \, ±2, \, ±3…\)

\[\underbrace{\Delta l = \left(m + \frac{1}{2}\right)\lambda }_{\text{destructuve interference}} \nonumber \]

为了\(m = 0, \, ±1, \, ±2, \, ±3…\)

图为示意图，显示波浪r1和r2穿过两个狭缝 S1 和 S2。波浪在屏幕上的公共点 P 处汇合。 — 图\(\PageIndex{5}\)：波浪沿着不同的路径从狭缝到屏幕上的公共点 P。当一条路径比另一条路径长半个波长时，就会发生破坏性干扰——波浪开始相位但相位不一致。当一条路径比另一条路径长整个波长时，就会发生构造干扰，波浪开始并相位到达。