2.A：几何光学和图像形成（答案）

Last updated
Save as PDF

Page ID: 202382

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

检查你的理解

概念性问题

1。虚拟图像无法投射到屏幕上。你不能仅仅通过眼睛感知到的图像来区分真实图像和虚拟图像。

3。是的，你可以拍摄虚拟图像。例如，如果你用平面镜拍摄反射物，你会得到一张虚拟图像的照片。相机聚焦进入镜头的光线以形成图像；光源是真实物体还是镜子的反射（即虚拟图像）都无关紧要。

5。不，你可以像看到虚拟图像一样看到真实图像。眼睛的视网膜可以有效地用作屏幕。

7。镜子的大小应该是你的一半，它的顶部边缘应该与你的眼睛高度一致。大小不取决于你与镜子的距离。

9。当物体处于无穷大时；参见镜像方程

11。 是的，负放大倍率只是意味着图像是颠倒的；这并不能阻止图像比物体大。例如，对于凹面镜，如果与物体的距离大于一个焦距但小于两个焦距，则图像将被反转和放大。

13。 答案可能有所不同

15。 镜头的焦距是固定的，因此图像距离随物体距离的变化而变化。

17。 是的，焦距会改变。镜头制造商的方程式表明，焦距取决于镜头周围介质的折射率。由于水的折射率与空气的折射率不同，因此当镜头浸入水中时，焦距会发生变化。

19。 放松的正常视力眼睛会将平行光线聚焦到视网膜上。

21。 拥有内置镜片的人需要戴眼镜才能阅读，因为他们的肌肉无法像使用生物镜片那样扭曲镜片，因此他们无法聚焦在附近的物体上。为了纠正近视，人工晶状体的功率必须小于摘除的晶状体的功率。

23。 显微镜可创建宏观大小的图像，因此几何光学适用。

25。 目镜将移动到离物镜稍远一点的地方，这样物镜形成的图像就会略高于目镜的焦距。

问题

27。

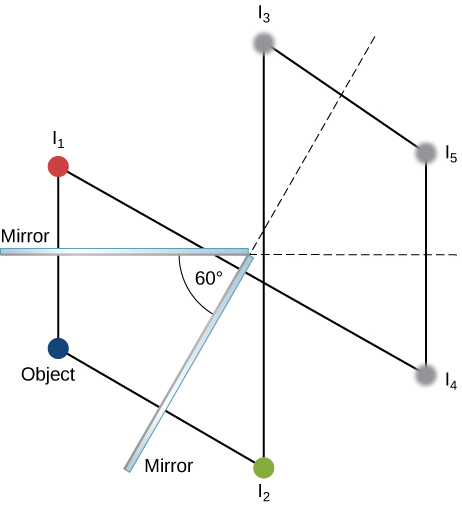
图中显示了两个反射镜的横截面，彼此成60度的角度。显示了标有物体 I1、I2、I3、I4 和 I5 的六个小圆圈。物体位于镜子之间的平分线上。线 1 与镜子 1 垂直相交，将物体连接到镜子另一侧的 I1。线 2 与镜子 2 垂直相交，将物体连接到镜子另一侧的 I2。与之平行的线路分别将 I2 连接到 I3，将 I1 连接到 I4。与之平行的线路分别将 I4 连接到 I5，将 I3 连接到 I5。 — 图中显示了两个反射镜的横截面，彼此成60度的角度。六个标有物体的小圆圈\(\displaystyle I_1, I_2, I_3, I_4\)，如图\(\displaystyle I_5\)所示。物体位于镜子之间的平分线上。线 1 与镜子 1 垂直相交，将物体连接到\(\displaystyle I_1\)镜子的另一侧。线 2 与镜子 2 垂直相交，将物体连接到镜子的\(\displaystyle I_2\)另一侧。与这些线平行的线分别\(\displaystyle I_2\)连接到\(\displaystyle I_3\)和连接\(\displaystyle I_1\)到\(\displaystyle I_4\)。与这些线平行的线分别\(\displaystyle I_4\)连接到\(\displaystyle I_5\)和连接\(\displaystyle I_3\)到\(\displaystyle I_5\)。

29。 它位于大镜子的焦点和小镜子的曲率中心。

31。 \(\displaystyle f=\frac{R}{2}⇒R=+1.60m\)

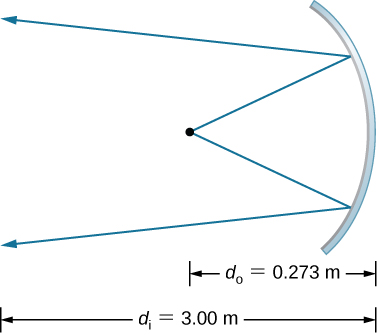
33。 \(\displaystyle d_o=27.3cm\)

35。 步骤 1：涉及镜像形成图像。

第 2 步：尽可能绘制问题设置。

第 3 步：使用薄透镜方程来解决这个问题。

第 4 步：找到 f。

第 5 步：给定：\(\displaystyle m=1.50,d_o=0.120m\)。

第 6 步：无需进行光线追踪。

步骤 7：使用\(\displaystyle m=\frac{d_i}{d_o},d_i=−0.180m\)。然后，\(\displaystyle f=0.360m\)。

步骤 8：图像是虚拟的，因为图像距离为负。焦距为正，所以镜子是凹的。

37。 a. 用于凸面镜\(\displaystyle d_i<0⇒m>0.m=+0.111\)；

b.\(\displaystyle d_i=−0.334cm\)（角膜后面）;

c.\(\displaystyle f=−0.376cm\)，这样\(\displaystyle R=−0.752cm\)

39。 \(\displaystyle m=\frac{h_i}{h_o}=−\frac{d_i}{d_o}=−\frac{−d_o}{d_o}=\frac{d_o}{d_o}=1⇒h_i=h_o\)

41。 \(\displaystyle m=−11.0\)\(\displaystyle A′=0.110m^2\)\(\displaystyle I=6.82kW/m^2\)

该图显示了凹面镜的横截面。来自某个点的两条光线撞击镜子并被反射。该点与镜子的距离标记为 d 下标 o = 0.273 m，d 下标 i = 3.00 m。 — 该图显示了凹面镜的横截面。来自某个点的两条光线撞击镜子并被反射。该点与镜像的距离标有\(\displaystyle d_o = 0.273m\)和\(\displaystyle d_i = 3.00m\)。

43。 \(\displaystyle x_{2m}=−x_{2m−1},(m=1,2,3,...),\)

\(\displaystyle x_{2m+1}=b−x_{2m},(m=0,1,2,...),\)和\(\displaystyle x_0=a.\)

45。 \(\displaystyle d_i=−55cm;m=+1.8\)

47。 \(\displaystyle d_i=−41cm,m=1.4\)

49。 证明

51。 a.\(\displaystyle \frac{1}{d_i}+\frac{1}{d_o}=\frac{1}{f}⇒d_i=3.43m\);

b.\(\displaystyle m=−33.33\)，这样还\(\displaystyle (2.40×10^{−2}m)(33.33)=80.0cm,\)有

\(\displaystyle (3.60×10^{−2}m)(33.33)=1.20m⇒0.800m×1.20m\)或者\(\displaystyle 80.0cm×120cm\)

53。 a.\(\displaystyle \frac{1}{d_o}+\frac{1}{d_i}=\frac{1}{f}\)\(\displaystyle d_i=5.08cm\);

b.\(\displaystyle m=−1.695×10^{−2}\)，所以最大高度为\(\displaystyle \frac{0.036m}{1.695×10^{−2}}=2.12m⇒100%\)；

c. 这似乎很合理，因为在 3.00 米处可以得到一个人的全长照片。

55。 a.\(\displaystyle \frac{1}{d_o}+\frac{1}{d_i}=\frac{1}{f}⇒d_o=2.55m\);

b。\(\displaystyle \frac{h_i}{h_o}=−\frac{d_i}{d_o}⇒h_o=1.00m\)

57。 a. 使用\(\displaystyle \frac{1}{d_o}+\frac{1}{d_i}=\frac{1}{f}\)，\(\displaystyle d_i=−56.67cm\)。然后我们可以确定放大倍率，\(\displaystyle m=6.67\)。

b.\(\displaystyle d_i=−190cm\) 和\(\displaystyle m=+20.0\)；

c. 随着物体朝焦距的距离增加，放大倍率 m 会迅速增加。

59。 \(\displaystyle \frac{1}{d_o}+\frac{1}{d_i}=\frac{1}{f}\)

\(\displaystyle d_I=\frac{1}{(1/f)−(1/d_o)}\)

\(\displaystyle \frac{d_i}{d_o}=6.667×10^{−13}=\frac{h_i}{h_o}\)

\(\displaystyle h_i=−0.933mm\)

61。 \(\displaystyle d_i=−6.7cm\)

\(\displaystyle h_i=4.0cm\)

63。 在聚合镜头右侧 83 厘米处，\(\displaystyle m=−2.3,h_i=6.9cm\)

65。 \(\displaystyle P=52.0D\)

67。 \(\displaystyle \frac{h_i}{h_o}=−\frac{d_i}{d_o}⇒h_i=−h_o(\frac{d_i}{d_o})=−(3.50mm)(\frac{2.00cm}{30.0cm})=−0.233mm\)

69。 a.\(\displaystyle P=+62.5D\);

b.\(\displaystyle \frac{h_i}{h_o}=−\frac{d_i}{d_o}⇒h_i=−0.250mm\);

c。\(\displaystyle h_i=−0.0800mm\)

71。 \(\displaystyle P=\frac{1}{d_o}+\frac{1}{d_i}⇒d_o=28.6cm\)

73。 最初，近距离视野是 51.0 D。因此，\(\displaystyle P=\frac{1}{d_o}+\frac{1}{d_i}⇒d_o=1.00m\)

75。 最初，\(\displaystyle P=70.0D\)；由于普通远距离视觉的功率为 50.0 D，因此功率应降低 20.0 D

77。 \(\displaystyle P=\frac{1}{d_o}+\frac{1}{d_i}⇒d_o=0.333m\)

79。 a.\(\displaystyle P=52.0D\);

b。\(\displaystyle P′=56.16D\)\(\displaystyle \frac{1}{d_o}+\frac{1}{d_i}=P⇒d_o=16.2cm\)

81。 我们需要\(\displaystyle d_i=−18.5cm\)时间\(\displaystyle d_o=∞\)，所以\(\displaystyle P=−5.41D\)

83。 让\(\displaystyle x\) = 远点 ⇒\(\displaystyle P=\frac{1}{−(x−0.0175m)}+\frac{1}{∞}⇒−xP+(0.0175m)P=1⇒x=26.8cm\)

85。 \(\displaystyle M=6×\)

87。 \(\displaystyle M=(\frac{25cm}{L})(1+\frac{L−ℓ}{f})\)\(\displaystyle L−ℓ=d_o\)\(\displaystyle d_o=13cm\)

89。 \(\displaystyle M=2.5×\)

91。 \(\displaystyle M=−2.1×\)

93。 \(\displaystyle M=\frac{25cm}{f}\)\(\displaystyle M_{max}=5\)

95。 \(\displaystyle M^{young}_{max}=1+\frac{18cm}{f}⇒f=\frac{18cm}{M^{young}_{max}−1}\)

\(\displaystyle M^{old}_{max}=9.8×\)

97。 a.\(\displaystyle \frac{1}{d_o}+\frac{1}{d_i}\)\(=\frac{1}{f}⇒d_i=4.65cm⇒m=−30.01\);

b。\(\displaystyle M_{net}=−240\)

99。 a. 在物镜\(\displaystyle \frac{1}{d^{obj}_o}+\)\(\frac{1}{d^{obj}_i}\)\(=\frac{1}{f^{obj}}\)\(⇒d^{obj}_i=18.3cm\)后面；

b.\(\displaystyle m^{obj}=−60.0\);

c。\(\displaystyle d^{eye}_o=1.70cm\)

\(\displaystyle d^{eye}_i=−11.3cm\);

d。\(\displaystyle M^{eye}=13.5\);

e。\(\displaystyle M_{net}=−810\)

101。 \(\displaystyle M=−40.0\)

103。 \(\displaystyle f^{obj}=\frac{R}{2},M=−1.67\)

105。 \(\displaystyle M=−\frac{f^{obj}}{f^{eye}},f^{eye}=+10.0cm\)

107。 答案会有所不同。

109。 距离镜子左侧 12 厘米，\(\displaystyle m=3/5\)

111。 镜子前 27 厘米\(\displaystyle m=0.6,h_i=1.76cm\)，直立方向

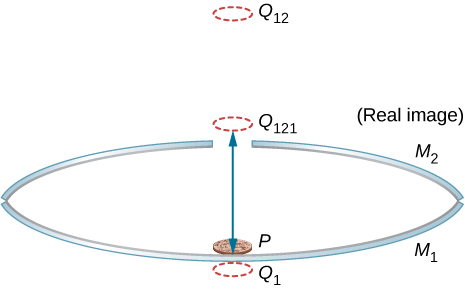
113。 下图显示了以镜像\(\displaystyle Q_1\)中的图像开头的三个连续图像\(\displaystyle M_1\)。 \(\displaystyle Q_1\)是镜中的镜像\(\displaystyle M_1\)，镜中的镜像\(\displaystyle M_2\)\(\displaystyle Q_{12}\)是镜中的镜像\(\displaystyle M_1\)是真实的图像\(\displaystyle Q_{121}\)。

图中显示了两个凹面反射镜 M1 和 M2 的侧视图，其中一个位于另一个之上，彼此面对。顶部 M2 中间有一个小洞。在底部镜子上放一分钱。标有 Q 下标 1 的便士图片显示在 M1 下方。顶镜上方显示了另一张标有 Q 下标 121 的便士图片。这被标记为真实图像。 — 该图显示了两个凹面镜的侧视图\(\displaystyle M_1\)，其中一个\(\displaystyle M_2\)位于另一个之上，彼此面对。顶部\(\displaystyle M_2\)，中间有一个小洞。在底部镜子上放一分钱。贴有便士标签的图像\(\displaystyle Q_1\)如下所示\(\displaystyle M_1\)。顶部镜子上方显示了另一张带有标签\(\displaystyle Q_{121}\)的便士图片。这被标记为真实图像。

115。 距离轴 5.4 厘米

117。 让凹面镜的顶点作为坐标系的原点。图片 1 的长度为 −10/3 厘米（−3.3 厘米），图片 2 的长度为 −40/11 厘米（−3.6 厘米）。它们作为后续图像的对象，分别为 −310/83 cm（−3.7 cm）、−9340/2501 cm（−3.7 cm）、−140,720/37,681 cm（−3.7 cm）。所有剩余图像的长度约为 −3.7 cm。

119。

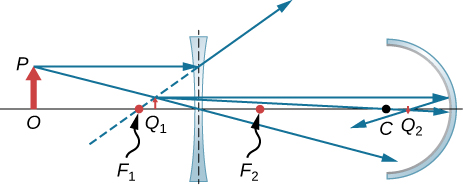
图从左至右显示：一个基准为O轴的物体，顶端为P。一个双凹镜头，焦点分别在左侧和右侧 F1 和 F2，以及一个曲率中心的凹面镜 C。两条光线起源于 P 并通过双凹透镜发散。它们的背部延伸部分在F1和镜头之间汇合，形成图像Q1。源自 Q1 尖端的两条光线撞击镜子，在 Q2 处反射并在 C 和镜子之间会聚。 — 图中显示了两个棱镜，它们的底座彼此平行，与水平方向成45度的角度。右边是一个双凸透镜。沿光轴的光线从左侧进入该设置，在两个棱镜之间偏离，并平行于光轴移动，略低于光轴。它进入镜头并偏离镜头以穿过另一侧的焦点。

121。 图从左至右显示：一个基准为O轴的物体，顶端为P。一个双凹镜头，焦点分别在左侧和右侧 F1 和 F2，以及一个曲率中心的凹面镜 C。两条光线起源于 P 并通过双凹透镜发散。它们的背部延伸部分在F1和镜头之间汇合，形成图像Q1。源自 Q1 尖端的两条光线撞击镜子，在 Q2 处反射并在 C 和镜子之间会聚。

123。 −5 D

125。 11

其他问题

127。 一个。

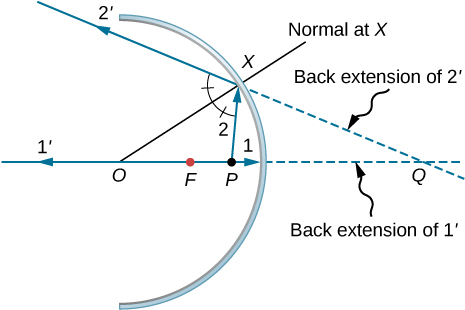
图中显示了曲率中心为 O 和焦点 F 的凹面镜的横截面。点 P 位于 F 点和反射镜之间的轴线上。射线 1 起源于 P 点，沿轴线移动并击中镜子。反射光线 1 素数沿轴向后移动。射线 2 起源于 P 并在 X 点击镜子。反射光线被标记为 2 素数。在 X 处标记为法线的 Line OX 将 PX 和 ray 2 素数形成的角度一分为二。 1 个素数和 2 个素数的向后延伸在 Q 点相交。

b。

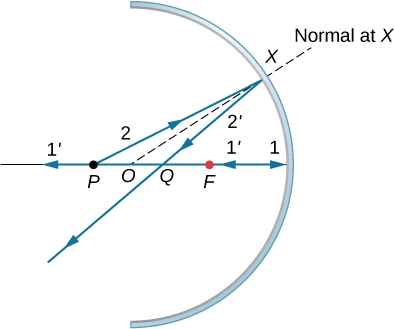
图中显示了点P、O、Q 和 F 位于光轴上的凹面镜的横截面。 P 点离镜子最远。射线 1 起源于 P，沿轴线移动并击中镜子。反射光线 1 素数沿轴向后移动。射线 2 起源于 P 并在点 X 处击中镜子。反射光线 2 素数在 Q 点处与轴相交，该点位于 P 点和 F 点之间，在 X 处标记为法线，将 PXQ 角度一分为二。

c。

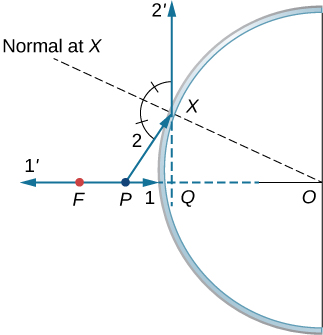
图中显示了一个凸面镜，其点 P 位于 F 点和光轴上的反射镜之间。射线 1 起源于 P，沿轴线移动并击中镜子。反射光线 1 素数沿轴向后移动。射线 2 起源于 P，在 X 点击镜子。反射光线 2 素数和 PX 形成的角度被 OX 一分为二，法线在 X 处。1 素数和 2 素数的背部延伸在 Q 点相交，就在镜子后面。

d. 与前一张照片相似，但焦距之外的点 P；

e. 对偏离轴的点物体重复 (a) — (d)。对于放置在与部件 (a) 和 (b) 相对应的凹面镜前偏离轴线的点物体，凸面镜的情况留作练习。

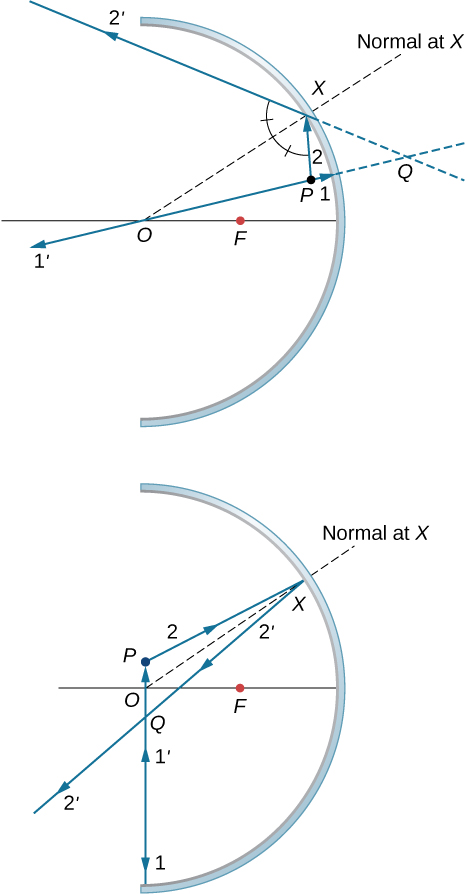
图 a 显示了凹面镜的横截面。点 P 位于轴线上方，比焦点 F 更靠近镜子。射线 1 起源于 P 并击中镜子。反射光线 1 prime 沿着与射线 1 相同的线向后移动，在 O 点与光轴相交。射线 2 起源于 P 点并在点 X 处击中镜子。反射光线被标记为 2 素数。 1 prime 和 2 prime 的背部延伸部分在镜子后面的 Q 点相交。射线 2 和 2 素数形成的角度被 OX 一分为二，X 处的法线图 b 显示了凹面镜的横截面。点 P 位于轴线上方，距离镜子比 F 点更远。射线 1 起源于 P 并击中镜子。反射光线 1 prime 沿着与射线 1 相同的线向后移动，在 O 点与光轴相交。射线 2 起源于 P 点并在点 X 处击中镜子。反射光线被标记为 2 素数。光线 1 素数和 2 素数在镜子前面的 Q 点相交。射线 2 和 2 素数形成的角度被 OX 一分为二，法线位于 X 处。

129。 \(\displaystyle d_i=−10/3cm,h_i=2cm\)，直立

131。 证明

133。

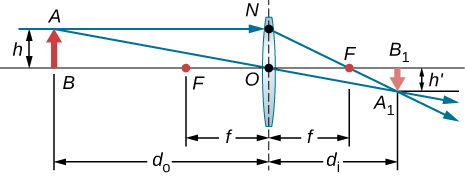
图中显示了双凸透镜、放置在光轴 A 点处的物体和在镜头后方轴线 B1 点处形成的倒置图像。物体的顶部是距原点的距离 h。三条光线从物体顶部发出，照射镜头，然后在倒置图像顶部的另一侧汇聚。它通过镜头前方的焦点，平行于镜头后面的光轴。 — 图中显示了双凸透镜、放置在光轴 A 点处的物体和在镜头后面的轴线\(\displaystyle B_1\)上点形成的倒置图像。物体的顶部是距原点的距离 h。三条光线从物体顶部发出，照射镜头，然后在倒置图像顶部的另一侧汇聚。它通过镜头前方的焦点，平行于镜头后面的光轴。

三角形 BAO 和三角形\(\displaystyle B_1A_1O\)是相似的三角形。因此，\(\displaystyle \frac{A_1B_1}{AB}=\frac{d_i}{d_o}\)。三角形 NOF 和三角形\(\displaystyle B_1A_1F\)是相似的三角形。因此，\(\displaystyle \frac{NO}{f}=\frac{A_1B_1}{d_i−f}\)。注意这\(\displaystyle NO=AB\)给了\(\displaystyle \frac{AB}{f}=\frac{A_1B_1}{d_i−f}\)或\(\displaystyle \frac{AB}{A_1B_1}=\frac{f}{d_i−f}\). 反过来可以得到\(\displaystyle \frac{A_1B_1}{AB}=\frac{d_i−f}{f}\). 将比率的两个表达式相等\(\displaystyle \frac{A_1B_1}{AB}\)可以得出\(\displaystyle \frac{d_i}{d_o}=\frac{d_i−f}{f}\)。除以 g\(\displaystyle d_i\) ives\(\displaystyle \frac{1}{d_o}=\frac{1}{f}−\frac{1}{d_i}\) 或\(\displaystyle \frac{1}{d_o}+\frac{1}{d_i}=\frac{1}{f}\)。

135。 70 厘米

137。 平面镜有无限的焦点，所以\(\displaystyle d_i=−d_o\)。镜中人的总视在距离将是他的实际距离，加上视在图像距离，或\(\displaystyle d_o+(−d_i)=2d_o\)。如果这个距离必须小于 20 厘米，他应该站在 20 厘米处\(\displaystyle d_o=10cm\)。

139。 我们想要这里\(\displaystyle d_o=25cm−2.20cm=0.228m\)。如果\(\displaystyle x=\)靠近点，\(\displaystyle d_i=−(x−0.0220m)\). 因此，\(\displaystyle P=\frac{1}{d_o}+\frac{1}{d_i}=\frac{1}{0.228m}+\frac{1}{x−0.0220m}\)。使用\(\displaystyle P=0.75D\)给\(\displaystyle x=0.253m\)出，因此近点为 25.3 厘米。

141。 假设镜头距离男孩的眼睛 2.00 cm，则图像距离必须为\(\displaystyle d_i=−(500cm−2.00cm)=−498cm\)。对于无限距离物体，所需的功率为\(\displaystyle P=\frac{1}{d_i}=−0.200D\)。因此，\(\displaystyle −4.00D\)镜头将校正近视。

143。 \(\displaystyle 87μm\)

145。 使用，\(\displaystyle M_{net}=−\frac{d^{obj}_i(f^{eye}+25cm)}{f^{obj}f^{eye}}\)。物镜的图像距离为\(\displaystyle d^{obj}_i=−\frac{M_{net}f^{obj}f^{eye}}{f^{eye}+25 \: cm}\)。使用\(f^{obj}=3.0cm\)\(f^{eye}=10cm\)、和 g\(M=−10\) ives\(\displaystyle d^{obj}_i=8.6cm\)。我们希望这张图像位于目镜的焦点，以便目镜在无限远处形成图像，以便舒适地观看。因此，镜头之间的距离 d 应为\(\displaystyle d=f^{eye}+d^{obj}_i=10cm+8.6cm=19cm\)

147。 a. 矫正镜头的焦距\(\displaystyle f_c=−80cm\)；

b. −1.25 D

149。 \(\displaystyle 2×10^{16}km\)

151。 \(\displaystyle 105m\)