2.9: 显微镜和望远镜

Last updated
Save as PDF

Page ID: 202350

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

在本节结束时，您将能够：

解释显微镜和望远镜操作背后的物理原理
描述这些仪器创建的图像并计算其放大倍数

显微镜和望远镜是主要的仪器，它们为我们当前对微观和宏观世界的理解做出了巨大贡献。这些设备的发明带来了物理学、天文学和生物学等学科的许多发现。在本节中，我们将解释使这些仪器起作用的基本物理学。

显微镜

尽管眼睛看见大大小小的物体的能力非常出色，但它所能检测到的最小细节显然受到限制。人们渴望用肉眼超越可能的视野，这促使人们使用了光学仪器。我们已经看到，一个简单的凸透镜可以创建放大的图像，但是用这样的镜头很难获得较大的放大倍率。如果不扭曲图像，大于 5 倍的放大倍率是很难的。为了获得更高的放大倍率，我们可以将简单的放大镜与一个或多个其他镜头结合使用。在本节中，我们将研究显微镜，这些显微镜可以放大肉眼看不到的细节。

显微镜最初是由荷兰和丹麦的眼镜制造商在1700年代初开发的。最简单的复合显微镜由两个凸透镜构成（图\(\PageIndex{1}\)）。物镜是短焦距（即高功率）的凸透镜，典型放大倍率为5倍至100倍。目镜，也称为目镜，是焦距较长的凸透镜。

显微镜的目的是创建小物体的放大图像，两个镜头都有助于最终的放大倍率。此外，最终放大的图像是在离观察者足够远的地方生成的，以便于观看，因为眼睛无法聚焦在距离太近（即比眼睛近点更近）的物体或图像上。

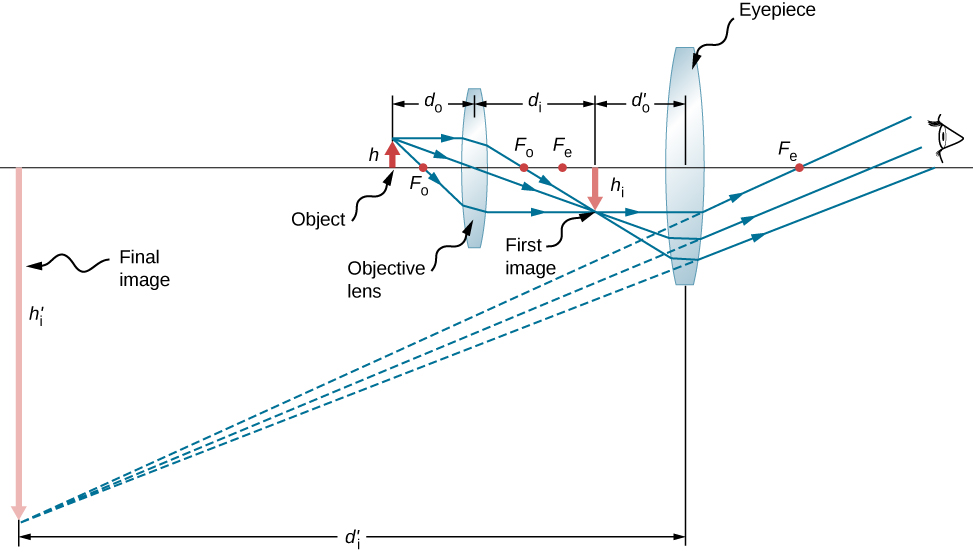
图从左至右显示：高度为 h 的物体、标有距离物镜 d 下标 o 的双凸透镜、高度为 h 的倒置图像 i 在距离物镜 d 下标 i 处标记第一张图像、距离物镜 d 下标 i 的双凸透镜从第一张图片中下标 o prime，最后是观察者的眼睛。光线从物体顶部发出，穿过物镜聚集在倒置图像的顶部。它们走得更远然后进入目镜，然后从那里偏离目镜到达眼睛。偏离光线的背面延伸汇聚在人物最左侧的大得多的倒置图像的尖端。这张图片的高度是 h 下标 i prime，它与目镜的距离是 d 下标 i prime。 — 图\(\PageIndex{1}\)：复合显微镜由两个镜头组成：物镜和目镜。物镜形成第一张图像，该图像比物体大。第一张图像位于目镜的焦距内，用作目镜的物体。目镜形成最终图像，可进一步放大。

要了解图中的显微镜是如何\(\PageIndex{1}\)形成图像的，请考虑其两个连续镜头。物体刚好超出了物镜\(f^{obj}\)的焦距，产生了比物体大的真实倒置图像。第一张图像用作第二个镜头或目镜的物体。目镜的定位使得第一张图像处于其焦距内\(f^{eye}\)，这样它就可以进一步放大图像。从某种意义上说，它充当放大镜，可以放大物镜产生的中间图像。目镜产生的图像是放大的虚拟图像。最终图像保持倒置状态，但距离观察者比物体更远，因此易于观看。

眼睛观察目镜创建的虚拟图像，目镜充当眼睛中镜头的物体。目镜形成的虚拟图像远远超出了眼睛的焦距，因此眼睛在视网膜上形成了真实的图像。

显微镜的放大倍率是物镜的线性放大倍率\(m^{obj}\)和目镜的角放大倍率的\(M^{eye}\)乘积。这些是由给出的

\ begin {align*}
&\ underbrace {m^ {o b j} =-\ frac {d_ {i} ^ {o b j}} {d_ {o b j}} {d_ {i} ^ {o b j}} _ {\ text {物镜线性放大}}\\
underbrace {M^ {e y e} =1+\ frac {25 c m} {f^ {e y e}} _ {\ text {目镜的角度放大}}
\end {align*}

这里\(f^{obj}\)和分别\(f^{eye}\)是物镜和目镜的焦距。我们假设最终图像是在眼睛的近点形成的，提供最大的放大倍率。请注意，目镜的角度放大倍率与之前为简单放大镜获得的角度放大倍率相同。这不足为奇，因为目镜本质上是一个放大镜，同样的物理学也适用于这里。复合显微镜\(M_{net}\)的净放大倍率是物镜的线性放大倍率和目镜角放大倍率的乘积：

\[ M_{\mathrm{net}}=m^{\mathrm{obj}} M^{\mathrm{eye}}=-\frac{d_{\mathrm{i}}^{\mathrm{obj}}\left(f^{\mathrm{eye}}+25 \mathrm{cm}\right)}{f^{\mathrm{obj}} f^{\mathrm{eye}}} \label{2.34} . \]

示例\(\PageIndex{1}\): Microscope Magnification

计算放置在具有 6.00 mm 焦距物镜和 50.0 mm 焦距目镜的复合显微镜上 6.20 mm 放置的物体的放大倍率。物镜和目镜相隔 23.0 cm。

策略

这种情况类似于图中所示的情况\(\PageIndex{1}\)。要找到整体放大倍率，我们必须知道物镜的线性放大倍率和目镜的角放大倍率。我们可以使用方程\ ref {2.34}，但我们需要使用薄镜方程来计算物镜\(d^{obj}_i\)的图像距离。

解决方案

求解\(d^{obj}_i\)给出的薄透镜方程

\ begin {align*} d^ {obj} _ {i} &=\ 左 (\ dfrac {1} {f^ {obj}} −\ dfrac {1} {d^ {obj} _o}\ 右) ^ {−1}\\ [5pt] &=\ 左 (\ dfrac {1} {6.00\, mm} −\ dfrac {1} {6.20mm}\ 右) ^ {−1}\\ [5pt] &=186\, mm\\ [5pt] &= 18.6\, cm\ end {align*}

将此结果与已知值一起插入方程\ ref {2.34}

\(f^{obj} = 6.00 \, mm = 0.600 \, cm\)
\(f^{eye} = 50.0 mm = 5.00 cm \)

给

\ begin {align*} M_ {net} &=−\ dfrac {d^ {obj} _i (f^ {eye} +25\, cm)} {f^ {obj} f^ {eye}}\\ [5pt] &=−\ dfrac {(18.6\, cm) (5.00\, cm)} {(0.600\, cm) (5.00\, cm)}\\ [5pt] &=−186\ end {align*}

意义

物镜和目镜都有助于整体放大倍率，整体放大倍率既大又负，与Figure一致\(\PageIndex{1}\)，在Figure中，图像被看作是大而反向的。在这种情况下，图像是虚拟的和反向的，单个元素不可能发生这种情况。

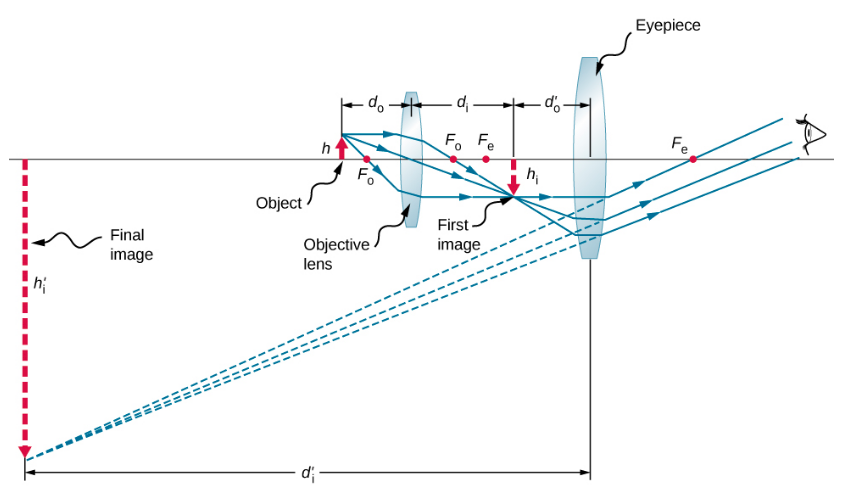
现在，我们计算图像处于无穷大状态时显微镜的放大倍数，如图所示\(\PageIndex{2}\)，因为这样可以最轻松地观看。显微镜的放大倍率是物镜的线性放大倍率\(m^{obj}\)和目镜角放大倍率\(M^{eye}\)的乘积。我们知道这一点

\[ m^{obj}=−\dfrac{d^{obj}_i}{d^{obj}_o} \nonumber \]

然后从薄透镜方程中我们得到

\[ m^{\mathrm{obj}}=-\frac{d_{\mathrm{i}}^{\mathrm{obj}}}{d_{\mathrm{o}}^{\mathrm{obj}}}=1-\frac{d_{\mathrm{i}}^{\mathrm{obj}}}{f^{\mathrm{obj}}}=\frac{f^{\mathrm{obj}}-d_{\mathrm{i}}^{\mathrm{obj}}}{f^{\mathrm{obj}}} \label{2.35}. \]

如果最终图像位于无限处，则物镜创建的图像必须位于目镜的焦点处。这可以通过考虑薄镜头方程来看出，\(d_i = \infty\)或者回想一下穿过焦点的光线彼此平行地离开镜头，这相当于在无限远处聚焦。对于许多显微镜来说，物镜的图像侧焦点与目镜物体侧焦点之间的距离标准化为 L = 16 cm。这个距离称为显微镜的管长。从图\(\PageIndex{2}\)中我们可以看出

\[ L=f^{obj}−d^{obj}_i . \nonumber \]

将其插入方程式\ ref {2.35} 会得出

\[ m^{obj}=\dfrac{L}{f^{obj}}=\dfrac{16cm}{f^{obj}}. \label{eq2.36} \]

我们现在需要计算目镜的角度放大倍率，图像为无穷大。为此，我们采用图像所对应的角度\(\theta_{object}\)与物体在眼睛近点（这是肉眼最接近物体能看到物体的角度，因此这是物体在视网膜上形成最大图像的位置\(\theta_{image}\)肉眼）。使用图形\(\PageIndex{2}\)并使用小角度近似值，我们有

\[ \theta_{i m a g e} \approx \frac{h_{i}^{o b j}}{f^{e y e}} \nonumber \]

和

\[ \theta_{\text {object}} \approx \frac{h_{i}^{o b j}}{25 c m} \nonumber \]

其中\(h_{i}^{obj}\)是物镜形成的图像的高度，物镜是目镜的物体。因此，目镜的角度放大倍率为

\[ M^{\text {eye }}=\frac{\theta_{\text {image }}}{\theta_{\text {object }}}=\frac{h_{i}^{\text {obj }}}{f^{\text {eye }}} \frac{25 \mathrm{cm}}{h_{i}^{\text {obj }}}=\frac{25 \mathrm{cm}}{f^{\text {eye }}} .\label{2.37} \]

因此，图像为无穷大的复合显微镜的净放大倍率为

\[ M_{net}=m^{obj}M^{eye}=−\dfrac{(16cm)(25cm)}{f^{obj}f^{eye}}. \label{2.38} \]

焦距必须以厘米为单位。减号表示最终图像是反向的。请注意，方程中唯一的变量是目镜和物镜的焦距，这使得该方程特别有用。

望远镜

望远镜用于观察远处的物体并生成比肉眼生成的图像更大的图像。望远镜收集的光比眼睛多得多，可以用更大的放大倍率和更好的分辨率观察昏暗的物体。望远镜是在1600年左右发明的，伽利略是第一个使用它们来研究天堂的望远镜，产生了巨大的后果。他观察了木星的卫星、月球上的陨石坑和山脉、黑子的细节以及银河系由大量恒星组成的事实。

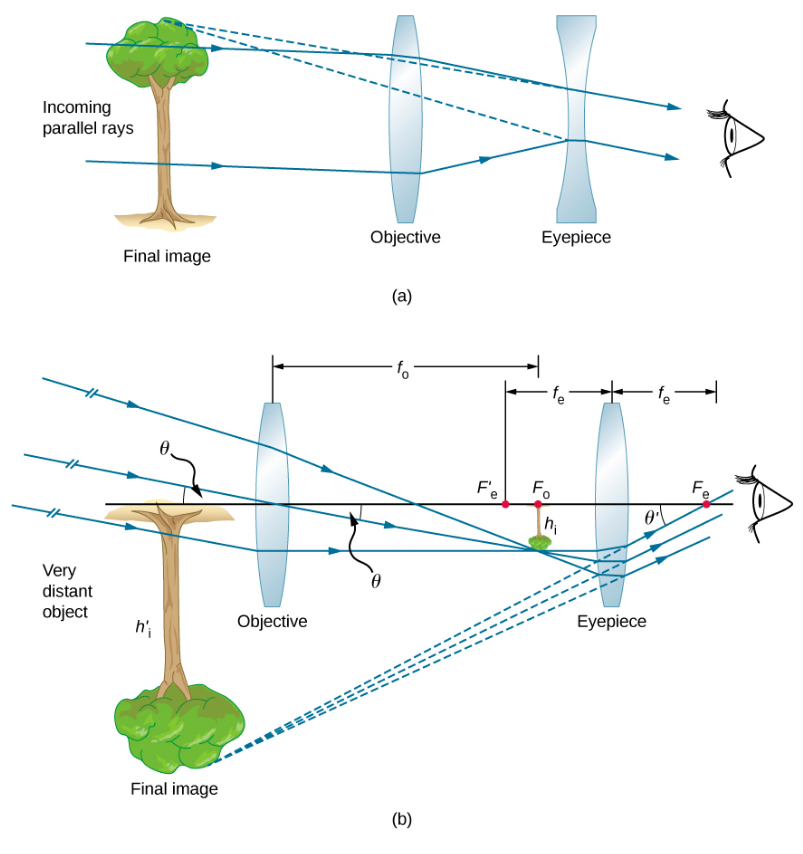
图 a 显示了从左侧传入的平行光线进入标有双凸透镜的物镜。从这里开始，它们相互偏离，进入标有目镜的双凹镜头，通过该镜头到达观察者的眼睛。在树的直立图像上，到达眼睛的光线的背部延伸向最左侧汇聚，标有最终图像。图 b 显示了与光轴成一定角度的入射光线从图左侧进入标有物镜的双凸透镜。它们在物镜的焦点处汇聚在另一边，形成一张微小的倒置树木图像。它们走得更远，进入标有目镜的双凸透镜。他们偏离这里进入眼睛。到达眼睛的光线与光轴形成一个角度 theta prime。它们的背部延伸部分会聚到最左边，这是一张放大的、倒置的树木图像，标有最终图像。 — 图\(\PageIndex{3}\)：（a）伽利略制造了带有凸面物镜和凹面目镜的望远镜。它们可以生成直立的图像，用于望远镜。 (b) 大多数简单的折射望远镜都有两个凸透镜。物镜在目镜的焦平面处（或正好在）处形成真实的倒置图像。该图像用作目镜的物体。目镜形成虚拟的倒置图像，经过放大。

图中\(\PageIndex{3a}\)显示了由两个透镜组成的折射望远镜。第一个镜头称为物镜，在第二个镜头（称为目镜）的焦距内形成真实图像。物镜的图像充当目镜的物体，目镜形成由眼睛观察的放大虚拟图像。这种设计是伽利略用来观察天堂的设计。

尽管折射望远镜中透镜的排列看起来与显微镜中的镜头排列相似，但两者之间存在重要差异。在望远镜中，真实物体很远，中间图像比物体小。在显微镜中，真实物体非常接近，中间图像比物体大。在望远镜和显微镜中，目镜都会放大中间图像；但是，在望远镜中，这是唯一的放大倍率。

最常见的双镜头望远镜如图所示\(\PageIndex{3b}\)。该物体离望远镜太远，以至于与镜头的焦距相比，它基本上处于无限远处\(d_{o}^{obj} \approx \infty \)，因此入射的光线基本上是平行的，聚焦在焦平面上。因此，第一张图像生成于

\[ d_{i}^{obj} = f^{obj} \nonumber \]

如图所示，与直接看物体可能看到的相比，它并不大。但是，望远镜目镜（如显微镜目镜）的目镜允许你比你的近点更接近第一张图像，因此会放大它（因为你离它很近，它会从你的眼睛倾斜一个更大的角度，因此在你的视网膜上形成更大的图像）。至于简单的放大镜，望远镜的角度放大倍率是图像所对应的角度（\(\theta_{image}\)英寸\(\PageIndex{3b}\)）与真实物体对应的角度（\(\theta_{object}\)英寸\(\PageIndex{3b}\)）之比：

\[ M=\dfrac{θ_{image}}{θ_{object}}. \label{2.39} \]

要获得仅涉及镜头参数的放大倍率表达式，请注意，物镜的焦平面与目镜的焦距非常接近。如果我们假设这些飞机是叠加的，则情况如图所示\(\PageIndex{4}\)。

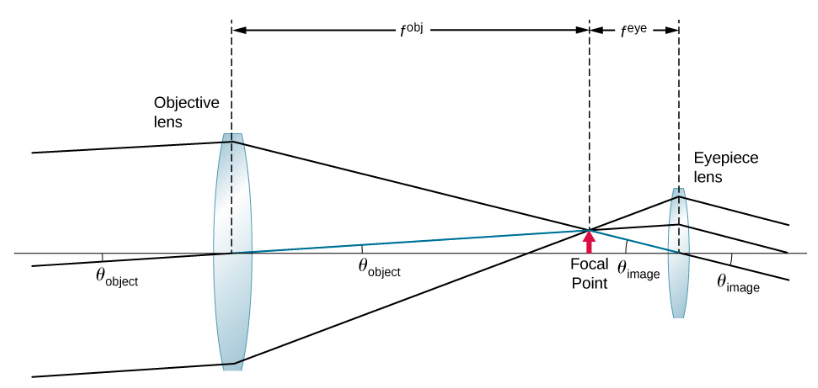
以一定角度 theta 下标物体的光线进入双凸物镜，然后在焦点的另一侧会聚。从这里，它们进入双凸目镜镜头，并以平行光线形式出现，形成与光轴成角度的theta下标图像。 — 图\(\PageIndex{4}\)：望远镜物镜的焦平面非常接近目镜的焦平面。通过\(\theta_{image}\)目镜观看的图像所对应的角度\(\theta_{object}\)大于用肉眼观察时物体所对应的角度。

我们进一步假设角度\(\theta_{object}\)和\(\theta_{image}\)很小，因此小天使近似值成立 (\(\tan \theta \approx \theta\))。如果在焦平面上形成的图像有高度，\(h\)那么

\ begin {array} {l}
\ theta_ {\ text {object}}\ 大约\ tan\ theta_ {\ text {object}} =\ frac {h} {f^ {\ text {image}} =\ frac {-h} {f^ {eye}}\ nonum
ber\ end {array}

这里引入了减号，因为如果我们沿逆时针方向测量两个角度，高度为负。将这些表达式插入方程\ ref {2.39} 可以得出

\[ M=\frac{-h_{\mathrm{i}}}{f^{\mathrm{eye}}} \frac{f^{\mathrm{obj}}}{h_{\mathrm{i}}}=-\frac{f^{\mathrm{obj}}}{f^{\mathrm{eye}}} \label{2.40}. \]

因此，为了获得最大的角放大倍率，最好使用长焦距的物镜和短焦距的目镜。角度放大倍率越大\(M\)，通过望远镜观察物体时会显得越大，从而可以看到更多的细节。对可观测细节的限制是由许多因素造成的，包括镜头质量和大气干扰。典型目镜的焦距为 2.5 厘米或 1.25 厘米。如果望远镜的物镜焦距为 1 米，则这些目镜的放大倍率分别为 40 倍和 80 倍。因此，角度放大倍率使图像看起来比真实物体近 40 倍或 80 倍。

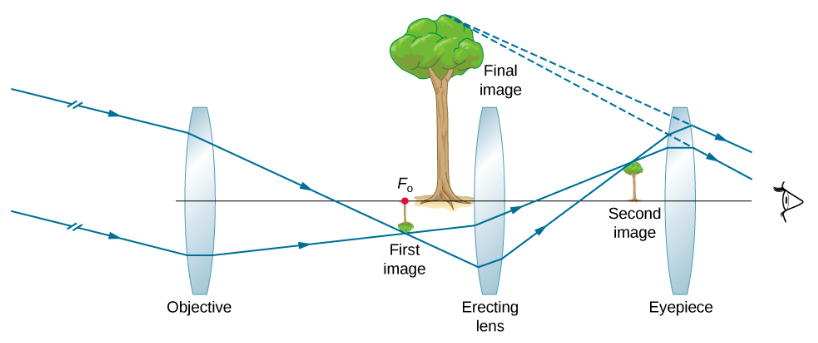
放大倍数中的减号表示图像是倒置的，这对于观测恒星并不重要，但对于其他应用（例如船上的望远镜或望远镜枪瞄准器）来说却是一个真正的问题。如果需要直立图像，则\(\PageIndex{3a}\)可以使用伽利略的排列方式。但更常见的安排是使用第三个凸透镜作为目镜，增加前两个凸透镜之间的距离，然后再次反转图像，如图所示\(\PageIndex{5}\)。

与光轴成一定角度的平行光线进入双凸物镜并在另一侧汇聚，形成物镜焦点处树木的微小倒置图像。从这里开始，光线穿过另一个标有竖立透镜的双凸透镜，然后在另一侧汇聚，形成树木的直立小图像。从这里，光线穿过双凸目镜进入眼睛。它们的背面延伸部分汇聚在一起，形成标有最终图像的树的放大直立图像。它位于第一张图像和竖立镜头之间。 — 图\(\PageIndex{5}\)：望远镜中三个镜头的排列可生成直立的最终图像。前两个镜头之间的距离足够远，以至于第二个镜头会反转第一个镜头的图像。第三个镜头充当放大镜，使图像保持直立并位于易于查看的位置。

世界上最大的折射望远镜是直径为40英寸的耶克斯望远镜，位于威斯康星州日内瓦湖（图\(\PageIndex{6}\)），由芝加哥大学运营。

建造大型折射望远镜非常困难且昂贵。您需要大型无缺陷镜头，这本身就是一项技术要求很高的任务。折射望远镜基本上看起来像一个带有支撑结构的管子，可以将其向不同的方向旋转。折射望远镜有几个问题。镜头的像差会导致图像模糊。此外，随着较大镜头的镜片变厚，吸收的光线会越来越多，这使得微弱的恒星更难观察。大型镜头也很重，在自身重量下会变形。根据艾萨克·牛顿的设计，折射望远镜的一些问题是通过避免折射来收集光线，而是使用曲面镜代替折射镜来解决的。这些望远镜被称为反射望远镜。

天文台中望远镜的照片。 — 图\(\PageIndex{6}\)：1897 年，美国威斯康星州耶克斯天文台建造了一台大型折射望远镜，其物镜直径为 40 英寸，管长 62 英尺。（来源：芝加哥大学耶克斯天文台）

反射望远镜

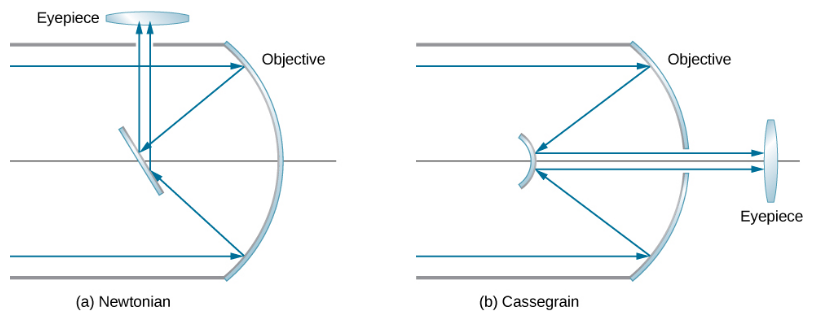
艾萨克·牛顿在1670年左右设计了第一台反射望远镜，以解决所有折射望远镜中发生的色差问题。在色差中，不同颜色的光在镜头中的折射量略有不同。结果，图像周围出现彩虹，图像显得模糊。在反射望远镜中，来自遥远光源的光线落在固定在管道底端的凹面镜的表面上。使用镜子代替镜头可以消除色差。凹面镜将光线聚焦在其焦平面上。设计问题是如何观察聚焦的图像。牛顿采用了一种设计，即来自凹面镜的聚焦光线被反射到管子的一侧，变成目镜（图\(\PageIndex{7a}\)）。这种安排在许多业余望远镜中很常见，被称为牛顿式设计。

有些望远镜使用凸面镜将光线反射回凹面镜中间。在这种布置中，聚光凹面镜中间有一个孔（\(\PageIndex{7b}\)）。然后，光线会入射到目镜镜头上。物镜和目镜的这种排列被称为卡塞格林设计。大多数大型望远镜，包括哈勃太空望远镜，都是这种设计的。其他安排也是可能的。在某些望远镜中，光探测器正好放置在曲面镜聚焦光线的地方。

图 a 显示平行光线照射凹面镜。它们相互反射和偏离。它们撞击倾斜的平面镜子，然后向上反射到双凸目镜上。图 b 显示平行光线照射凹面镜。它们相互反射和偏离。它们撞击一个较小的凸面镜，然后以平行光线的形式反射回凹面镜，彼此靠得更近。它们穿过凹镜中的缝隙，到达双凸目镜。 — 图\(\PageIndex{7}\)：反射望远镜：（a）在牛顿设计中，目镜位于望远镜的侧面；（b）在卡塞格林设计中，目镜位于主镜孔的后方。

现在，大多数天文研究望远镜都是反射式望远镜。最早的此类大型望远镜之一是建造在南加州帕洛玛山上的Hale 200英寸（或5米）望远镜，它有一面直径为200英寸的镜子。世界上最大的望远镜之一是位于夏威夷休眠莫纳克亚火山顶上的凯克天文台的 10 米凯克望远镜。凯克天文台操作两台 10 米长的望远镜。每面都不是一面镜子，而是由 36 个六角镜组成。此外，凯克号上的两台望远镜可以协同工作，从而将它们的功率提高到有效的 85 米镜面。哈勃望远镜（图\(\PageIndex{8}\)）是另一台大型反射望远镜，主镜直径为 2.4 米。哈勃于1990年被送入环绕地球的轨道。

哈勃望远镜的照片。 — 图\(\PageIndex{8}\)：从发现号航天飞机上看到的哈勃太空望远镜。（来源：美国宇航局对作品的修改）

反射望远镜\(M\)的角放大倍率也由方程\ ref {eq2.36} 给出。对于球面镜，焦距是曲率半径的一半，因此制作大型物镜不仅可以帮助望远镜收集更多的光，还可以增加图像的放大倍率。