2.8: 简单放大镜
- Page ID
- 202365
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)在本节结束时，您将能够：
- 了解简单放大镜的光学特性
- 描述由简单放大镜创建的图像
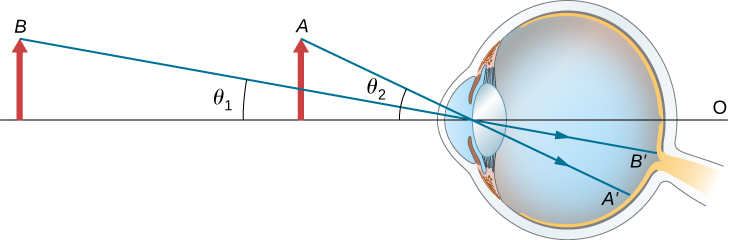
眼睛感知到的物体的表观大小取决于物体与眼睛的对角度。 如图所示\(\PageIndex{1}\)，物体与眼睛的对角比它在点处的位置要大\(B\)。\(A\) 因此，物体在\(A\)视网膜上形成的图像（参见\(OA′\)）比其放置时要大\(B\)（见\(OB′\)）。 因此，与眼睛倾斜较大角度的物体会显得更大，因为它们在视网膜上形成了更大的图像。
我们已经看到，当一个物体被放置在凸透镜的焦距内时，它的图像是虚拟的、直立的，并且比物体大（参见本图（b）部分）。 因此，当凸透镜产生的这种图像作为眼睛的物体时，如图所示\(\PageIndex{2}\)，视网膜上的图像会被放大，因为镜头产生的图像在眼睛中的倾角比物体大。 用于此目的的凸透镜称为放大镜或简单的放大镜。
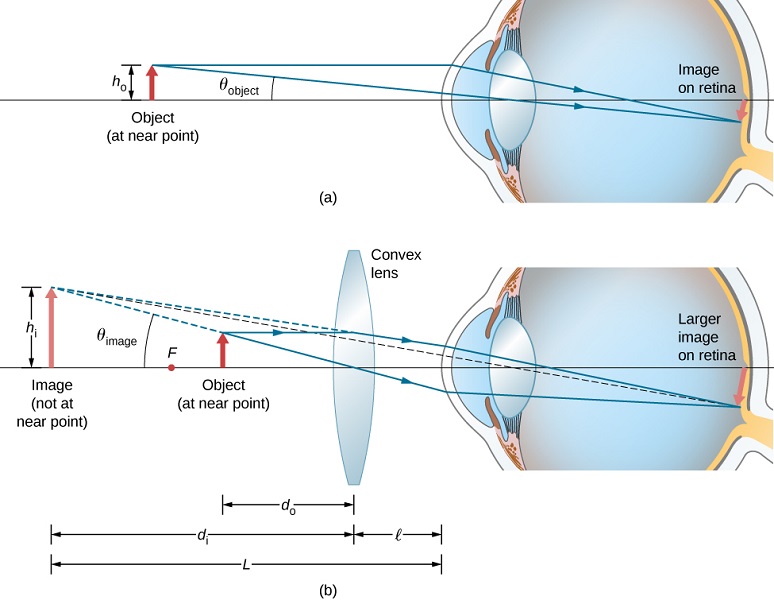
为了考虑放大镜的放大倍数，我们将图像（由镜头创建）所对应的角度与物体对角度（不使用镜头观看）进行比较，如图所示\(\PageIndex{1a}\)。 我们假设物体位于眼睛的近点，因为这是肉眼可以在视网膜上形成最大图像的物体距离。 我们将把镜头生成的放大图像与肉眼的最大图像尺寸进行比较。 当被眼睛观察时，图像的放大倍率是角度放大倍率\(M\)，它由图像所对应的角度\(θ_{image}\)与物体对应角度的\(θ_{object}\)比率来定义：
\[M=\dfrac{θ_{image}}{θ_{object}}. \nonumber \]
考虑图中所示的情况\(\PageIndex{1b}\)。 放大镜与眼睛保持一定距\(ℓ\)离，放大镜产生的图像与眼睛形成一定距\(L\)离。 我们想计算任意\(L\)和的角放大倍率\(ℓ\)。 在小角度近似值中，图像\(θ_{image}\)的角度大小为\(h_i/L\)。 近点物\(θ_{object}\)体的角度大小为\(θ_{object}=h_o/25\,cm\)。 然后角放大倍率是
\[\underbrace{ M=\dfrac{θ_{image}}{θ_{object}}=\dfrac{h_i(25cm)}{Lh_o}}_{\text{angular magnification}} . \label{angular magnification} \]
使用线性放大倍率的定义
\[m=−\dfrac{d_i}{d_o}=\dfrac{h_i}{h_o} \label{mag} \]
\[\dfrac{1}{d_o}+\dfrac{1}{d_i}=\dfrac{1}{f} \nonumber \]
我们得出放大镜角度放大倍率的以下表达式：
\[\begin{align} M&= \left(−\dfrac{d_i}{d_o}\right)\left(\dfrac{25\,cm}{L}\right) \\[4pt] &=−d_i\left(\dfrac{1}{f}−\dfrac{1}{d_i}\right)\left(\dfrac{25\,cm}{L}\right) \\[4pt] &= \left(1−\dfrac{d_i}{f}\right)\left(\dfrac{25\,cm}{L}\right) \label{eq10} \end{align} \]
从图\(\PageIndex{1b}\)中可以看出，图像距离的绝对值为\(|d_i|=L−ℓ\)。 请注意，\(d_i<0\)因为图像是虚拟的，所以我们可以通过显式插入减号来省去绝对值：
\[−d_i=L−ℓ. \label{eq34} \]
将方程\ ref {eq34} 插入方程\ ref {eq10} 为我们提供了放大镜角放大倍率的最终方程：
\[M=\left(\dfrac{25\,cm}{L}\right) \left(1+\dfrac{L−ℓ}{f} \right). \label{eq12} \]
请注意，该方程中的所有量都必须以厘米表示。 通常，我们希望图像处于近点距离（例如\(L=25\,cm\)）以获得最大放大倍率，并将放大镜放在靠近眼睛的地方（\(ℓ=0\)）。 在这种情况下，方程\ ref {eq12} 给出
\[M=1+\dfrac{25\,cm}{f} \label{eq13} \]
这表明最大放大倍率出现在焦距最短的镜头上。 此外，当图像处于近点距离并且镜头靠近眼睛 (\(ℓ=0\)) 时\(L=d_i=25\,cm\)，方程\ ref {eq12} 变成
\[M=\dfrac{h_i}{h_o}=m \label{eq14} \]
其中\(m\)是先前为球面反射镜和薄透镜得出的线性放大倍率（方程\ ref {mag}）。 另一个有用的情况是当图像处于无穷大 (\(L=\infty\)) 时。 然后，方程\ ref {eq12} 采用以下形式
\[M(L=\infty)=\dfrac{25\,cm}{f}. \label{eq15} \]
由此产生的放大倍率只是近点距离与放大镜头焦距之比，因此焦距较短的镜头可提供更强的放大倍率。 尽管此放大倍率比图像在近点获得的放大倍率小 1，但它提供了最舒适的观看条件，因为在观察远处的物体时眼睛会放松。
通过比较方程\ ref {eq13} 和\ ref {eq15}，我们可以看到给定会聚透镜的角放大范围为
\[\dfrac{25cm}{f} ≤ M ≤1+\dfrac{25cm}{f}. \nonumber \]
珠宝商希望用放大镜检查直径为 3.0 毫米的钻石。 钻石放在珠宝商的近点（25 厘米）处，珠宝商将放大镜放在眼睛附近。
- 要看到直径为 15 毫米的钻石图像，放大镜的焦距应该是多少？
- 要获得 10 倍放大倍率，放大镜的焦距应该是多少？
策略
我们需要确定放大镜所需的放大倍数。 因为珠宝商将放大镜放在眼睛附近，所以我们可以使用方程式\ ref {eq13} 来找出放大镜的焦距。
解决方案
a. 所需的线性放大倍率是所需图像直径与钻石实际直径的比率（方程\ ref {eq15}）。 因为珠宝商将放大镜放在眼睛附近，图像在他的近点形成，所以线性放大倍率与角度放大倍率相同，所以
\[\begin{align*} M &=m=\dfrac{h_i}{h_o}\\[4pt] &=\dfrac{15\,mm}{3.0\,mm} \\[4pt] &=5.0.\end{align*} \nonumber \]
放大镜的焦距 f 可以通过求解方程\ ref {eq13} 来计算\(f\)，这给出了
\[M=1+\dfrac{25\,cm}{f} \nonumber \]
\[\begin{align*} f&=\dfrac{25\,cm}{M−1} \\[4pt] &= \dfrac{25\,cm}{5.0−1} \\[4pt] &= 6.3\,cm \end{align*} \nonumber \]
b. 为了使图像放大十倍，我们再次求解方程\ ref {eq13}\(f\)，但这次我们使用\(M=10\)。 结果是
\[\begin{align*} f &=\dfrac{25\,cm}{M−1} \\[4pt] &=\dfrac{25\,cm}{10−1} \\[4pt] &=2.8\,cm. \end{align*} \nonumber \]
意义
请注意，使用焦距较小的镜头可以获得更大的放大倍率。 因此，我们需要使用曲率半径小于几厘米的镜头，并将其保持在离眼睛很近的地方。 这不是很方便。 下一节将探讨的复合显微镜可以克服这个缺点。