2.7: 相机
- Page ID
- 202351
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)在本节结束时，您将能够：
- 描述相机的光学元件
- 描述相机创建的图像
相机在我们的日常生活中很常见。 1825 年至 1827 年间，法国发明家 Nicéphore Niépce 成功拍摄了一张由原始相机创建的图像。 从那时起，在相机和基于摄像机的探测器的设计方面取得了巨大进展。
最初，照片是使用氯化银或溴化银等银基化合物的光敏反应记录的。 在 20 世纪 80 年代数码摄影问世之前，银基相纸一直很常用，数码摄影与电荷耦合器件 (CCD) 探测器密切相连。 简而言之，CCD是一种半导体芯片，它将图像记录为由微小像素组成的矩阵，每个像素位于表面的 “垃圾箱” 中。 每个像素都能够检测冲击它的光强度。 色彩是通过在像素上放置红色、蓝色和绿色滤镜来发挥作用，从而生成彩色数字图像（图\(\PageIndex{1}\)）。 在最佳分辨率下，一个 CCD 像素对应于图像的一个像素。 为了降低分辨率和减小文件的大小，我们可以将几个 CCD 像素 “合并” 为一个，从而生成一个更小但 “像素化” 的图像。
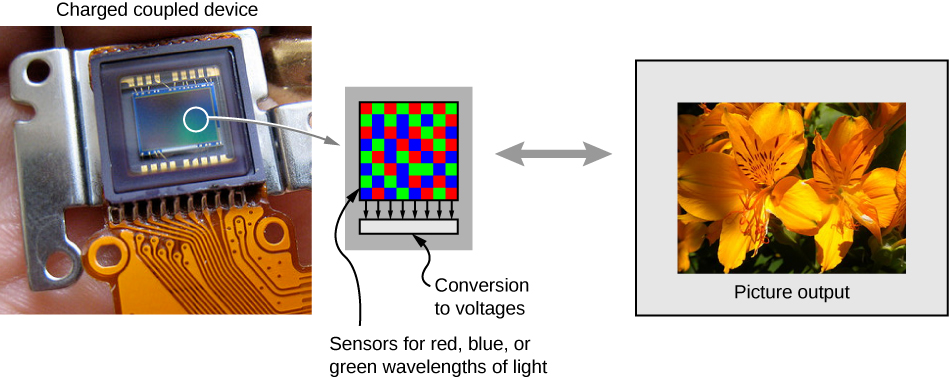
显然，电子学是数码相机的重要组成部分；但是，基础物理学是基础光学。 事实上，相机的光学效果与单镜头的光学镜头几乎相同，单镜头的物体距离明显大于镜头的焦距（图\(\PageIndex{2}\)）。
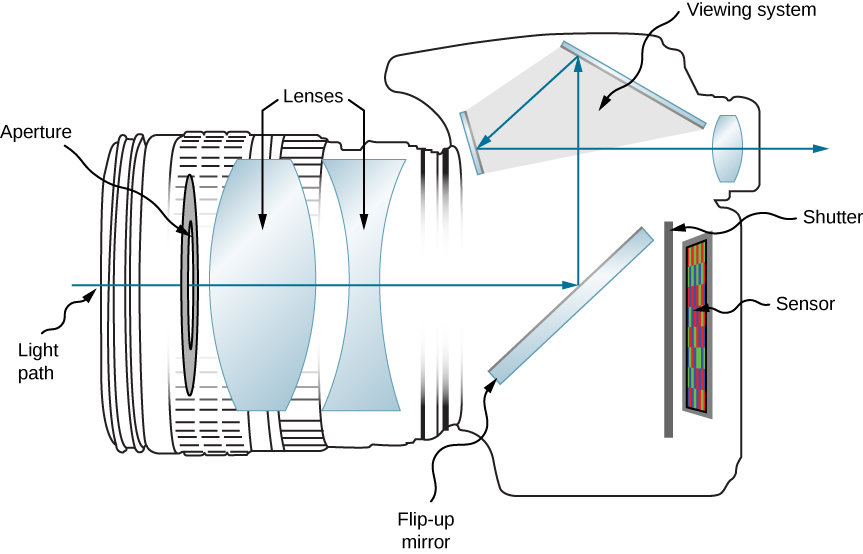
例如，让我们考虑一下智能手机中的摄像头。 普通的智能手机摄像头配备固定广角镜头，焦距约为4—5 mm。 （这个焦距大约等于手机的厚度。） 镜头生成的图像聚焦在安装在手机另一侧的 CCD 探测器上。 在手机中，镜头和 CCD 不能相对于彼此移动。 那么，我们如何确保远处和近距离物体的图像都对焦呢？
回想一下，人眼可以通过改变焦距来适应远距离和近距离的图像。 手机摄像头无法做到这一点，因为从镜头到探测器的距离是固定的。 这就是小焦距变得重要的地方。 假设我们有一台焦距为 5 mm 的相机。 自拍的图像距离是多少？ 自拍的物体距离（手持手机的长度）约为 50 cm。 使用薄透镜方程，我们可以这样写
\[\frac{1}{5mm}=\frac{1}{500mm}+\frac{1}{d_i} \nonumber \]
然后我们得到图像距离：
\[\frac{1}{d_i}=\frac{1}{5mm}−\frac{1}{500mm} \nonumber \]
请注意，物体距离比焦距大 100 倍。 我们可以清楚地看到，1/（500 mm）项明显小于1/（5 mm），这意味着图像距离几乎等于镜头的焦距。 实际计算得出的图像距离 d i =5.05mm。 该值非常接近镜头的焦距。
现在让我们考虑一下遥远物体的情况。 假设我们想拍一张站在离我们大约 5 米处的人的照片。 再次使用薄镜头方程，我们得出5.005 mm的图像距离。 物体离镜头越远，图像距离越近。 在无限远物体的极限情况下，我们得到的图像距离完全等于镜头的焦距。
如你所见，自拍的图像距离和远处物体的图像距离之间的差异约为0.05 mm或50微米。 即使是较短的物体距离，例如手的长度，也比镜头的焦距大两个数量级，从而导致图像距离的微小变化。 （50 微米的差异小于普通纸张的厚度。） 如此微小的差异可以由位于镜头焦距处的同一个探测器轻松容纳。 图像分析软件可以帮助提高图像质量。
传统的即拍相机通常使用可移动镜头来改变镜头与图像的距离。 较昂贵的镜面反光相机的复杂镜头可以提供高质量的摄影图像。 这些相机镜头的光学效果超出了本教科书的范围。