2.6: 眼睛
- Page ID
- 202383
在本节结束时,您将能够:
- 了解人眼如何形成图像的基本物理原理
- 认识几种视力受损状况以及治疗这些疾病的光学原理
眼睛的物理学
眼睛在形成图像的方式以及它可以检测到的丰富细节和色彩方面都非常出色。 但是,我们的眼睛经常需要一些矫正才能达到所谓的 “正常” 视力。 实际上,正常视力应该被称为 “理想” 视力,因为将近一半的人口需要某种视力矫正,因此需要戴眼镜绝不是 “异常”。 可以使用本章前面讨论的光学器件来分析我们的眼睛形成的图像和常见的视力校正。
该图\(\PageIndex{1}\)显示了眼睛的基本解剖结构。 角膜和晶状体形成了一个系统,可以很好地近似地说,它充当单个薄透镜。 为了获得清晰的视野,必须将真实图像投射到光敏视网膜上,该视网膜与镜头保持固定距离。 灵活的眼睛镜头允许它调整镜头的曲率半径,从而在视网膜上为不同距离的物体生成图像。 图像的中心落在中央凹上,中央凹在视野中具有最大的光受体密度和最大的敏锐度(清晰度)。 眼睛的可变开口(即瞳孔),加上化学适应性,使眼睛能够探测到从最低可观测到的 10 倍(无损伤)的光强度。 这是一个令人难以置信的探测范围。 视觉神经冲动的处理从视网膜中的相互连接开始,然后在大脑中继续。 视神经将眼睛接收到的信号传送到大脑。
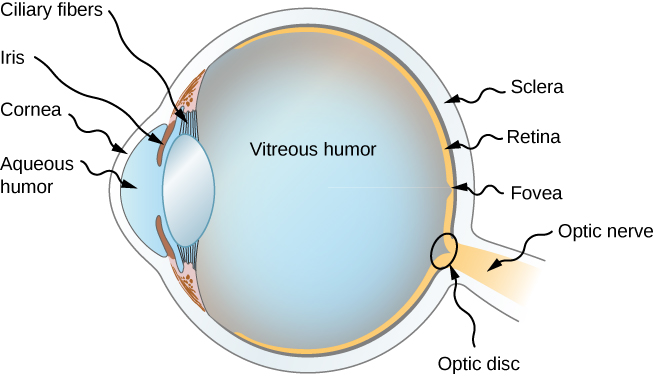
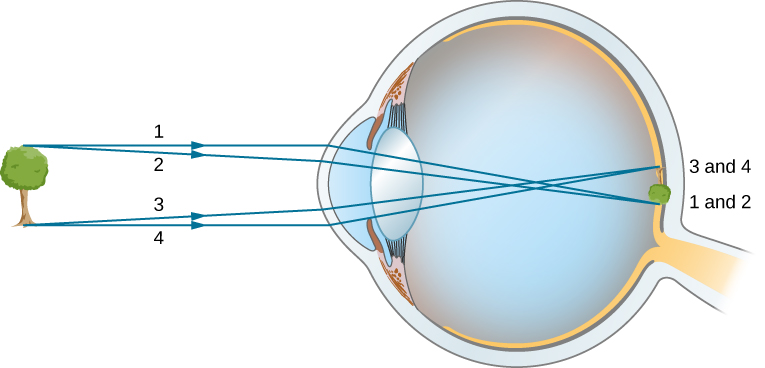
眼睛的折射指数对其形成图像的能力至关重要。 表中\(\PageIndex{1}\)列出了与眼睛相关的折射指数。 折射率(光线最弯曲的地方)的最大变化发生在空气角膜界面,而不是水性幽默镜头界面。 图中的射线图\(\PageIndex{2}\)显示了眼角膜和晶状体形成的图像。 角膜本身就是一个聚焦透镜,焦距约为 2.3 cm,它提供了眼睛的大部分聚焦能力。 该镜头是一种聚焦镜头,焦距约为6.4厘米,可提供在视网膜上产生清晰图像所需的更精细的对焦。 角膜和晶状体可以被视为单个薄晶状体,尽管光线会穿过多层材料(例如角膜、房水、晶状体中的几层和玻璃体),并在每个界面改变方向。 形成的图像与单凸透镜(即真实的倒置图像)产生的图像非常相似。 尽管眼睛中形成的图像是倒置的,但大脑会再次将其反转以使它们看起来直立。
| 材质 | 折射率 |
|---|---|
| 水 | 1.33 |
| 空气 | 1.0 |
| 角膜 | 1.38 |
| 水性幽默 | 1.34 |
| 镜头 | 1.41 * |
| 玻璃体幽默 | 1.34 |
如前所述,图像必须精确落在视网膜上才能产生清晰的视觉——也就是说,图像距离 d i 必须等于镜头与视网膜的距离。 由于镜头到视网膜的距离没有变化,因此所有距离的物体的图像距离 d i 都必须相同。 睫状肌调整眼镜的形状,以聚焦附近或远处的物体。 通过改变眼镜的形状,眼睛会改变镜头的焦距。 这种眼睛的机制被称为调节。
可以放置物体以便眼睛可以在视网膜上形成清晰图像的最近点称为眼睛的近点。 同样,远点是物体清晰可见的最远距离。 视力正常的人可以在 25 厘米到基本无限远的距离内清楚地看到物体。 临近点随着年龄的增长而增加,对于一些老年人来说,临近点变为几米。 在本文中,我们认为近点为 25 cm。
我们可以使用薄透镜方程来定量检查眼睛形成的图像。 首先,我们将镜头的光功率定义为
\[P=\frac{1}{f} \nonumber \]
焦距 f 以米为单位给出。 光功率单位称为 “屈光度”(D)。 也就是说,1d=1/m 或 1m −1。 验光师以屈光度为单位开出普通眼镜和隐形眼镜的处方。 有了这个光功率的定义,我们可以将薄透镜方程改写为
\[P=\frac{1}{d_o}+\frac{1}{d_i}. \nonumber \]
使用光功率很方便,因为对于两个或多个靠近的镜头,镜头系统的有效光功率大约是各个镜头光功率的总和:
\[P_{total}=P_{lens~1}+P_{lens~2}+P_{lens~3}+⋯ \label{sumlens} \]
角膜和眼镜的焦距分别为2.3和6.4厘米。 找出眼睛的净焦距和光功率。
策略
因此,间隔紧密的镜头的光学功率增加了\(P_{eye}=P_{cornea}+P_{lens}\)。
解决方案
用焦距写出功率方程可以得出
\[\frac{1}{f_{eye}}=\frac{1}{f_{cornea}}+\frac{1}{f_{lens}}=\frac{1}{2.3cm}+\frac{1}{6.4cm} \nonumber. \nonumber \]
因此,眼睛(角膜和晶状体加在一起)的焦距为
\[f_{eye}=1.69cm. \nonumber \]
眼睛的光功率是
\[P_{eye}=\frac{1}{f_{eye}}=\frac{1}{0.0169m}=59D. \nonumber \]
为了获得清晰的视野,图像距离\(d_i\)必须等于镜头到视网膜的距离。 距离\(d_o=25\, cm\)无限远的物体可以正常视野。 以下示例显示如何计算放置在眼睛附近点的物体的图像距离。
特定人眼的净焦距为 1.7 cm。 物体被放置在眼睛的近点。 聚焦图像在镜头后面形成的距离有多远?
策略
近点距离眼睛 25 厘米,因此物体距离为 d o =25 cm。 我们根据镜头方程确定图像距离:
\[\frac{1}{d_i}=\frac{1}{f}−\frac{1}{d_o}. \nonumber \]
解决方案
\[d_i=(\frac{1}{f}−\frac{1}{d_o})^{−1} \nonumber \]
\[=(\frac{1}{1.7cm}−\frac{1}{25cm})^{−1} \nonumber \]
\[=1.8cm \nonumber \]
因此,图像在镜头后方1.8厘米处形成。
意义
从放大倍率公式中,我们发现\(m=−\frac{1.8cm}{25cm}=−0.073\)。 由于 m<0,图像相对于物体的方向是反向的。 从 m 的绝对值可以看出,图像比物体小得多;实际上,它只有物体大小的 7%。
视力矫正
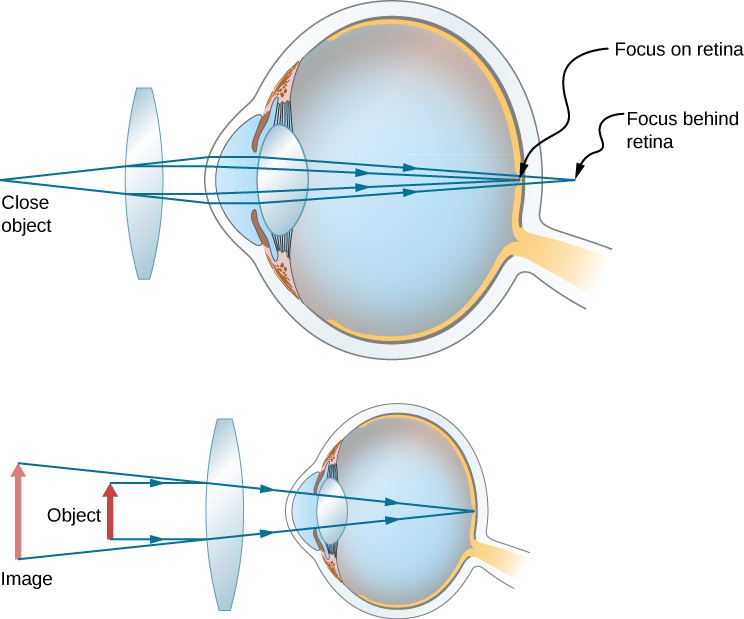
对某种视力矫正的需求非常普遍。 使用几何光学,典型的视觉缺陷很容易理解,有些则很容易纠正。 该图\(\PageIndex{3}\)说明了两种常见的视觉缺陷。 近视或近视是指看到近距离物体的能力,而远处的物体是模糊的。 眼睛会聚来自远处物体的几乎平行的光线,光线在视网膜前面穿过。 来自近距离物体的更多发散光线会聚在视网膜上,以获得清晰的图像。 与能清晰看到的最远物体的距离称为眼睛的远点(通常远点位于无穷大)。 远视或远视是指能够清楚地看到远处的物体,而近距离物体是模糊的。 有远见的眼睛无法充分汇聚来自附近物体的光线,无法使光线在视网膜上相遇。
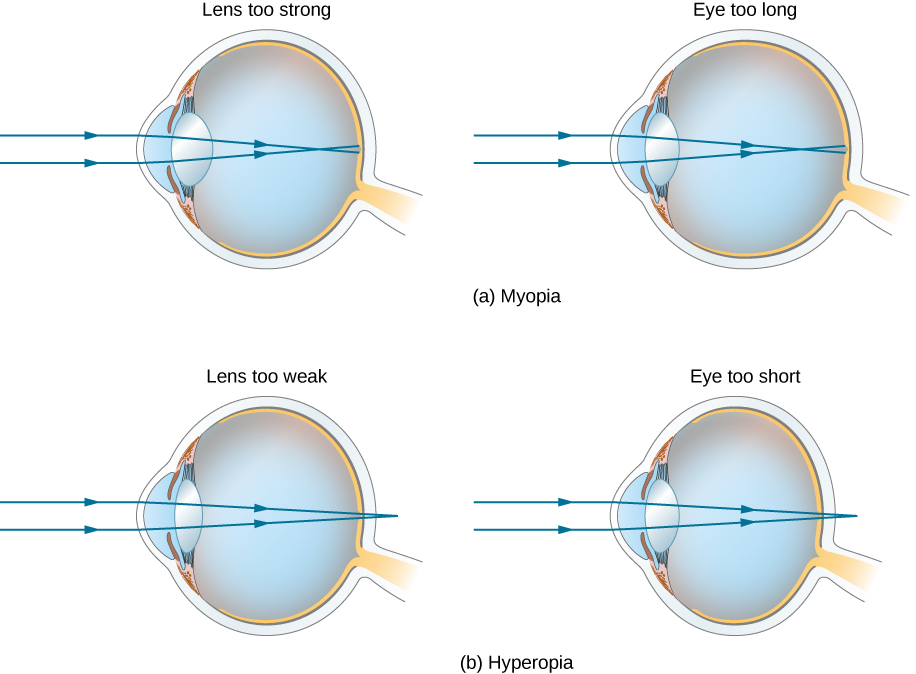
由于近视的眼睛会聚光线,因此近视校正包括在眼前放置一个发散的眼镜镜片,如图所示\(\PageIndex{4}\)。 这会降低太强的眼睛的光功率(回想一下,发散镜头的焦距是负的,所以它的光功率是负的)。 理解这种校正的另一种方法是,发散镜头会使入射光线发散得更多,以补偿眼睛镜头系统造成的过度收敛。 发散眼镜镜头产生的图像充当眼睛的(光学)物体,并且由于眼睛无法聚焦在其远点以外的物体上,因此发散镜头必须在比远点更近的点形成远处(物理)物体的图像。
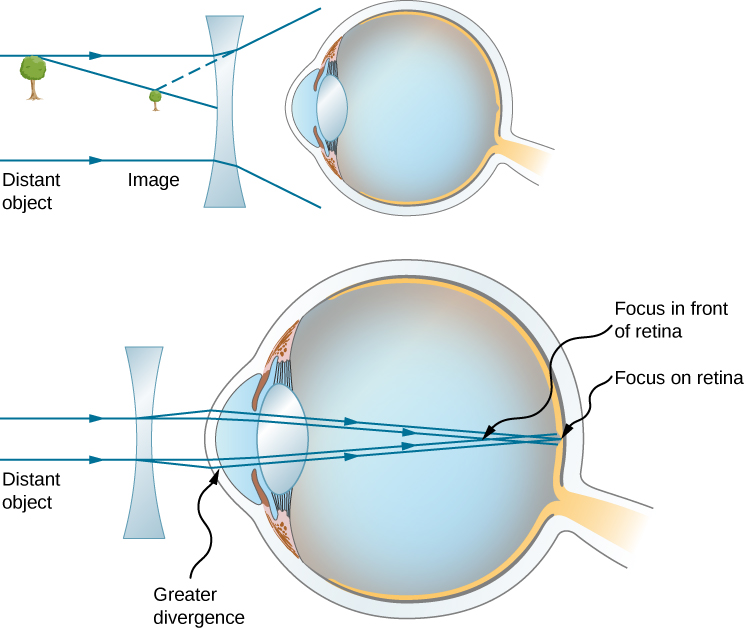
眼镜镜片需要多大的光学功率才能校正远点为30.0 cm的近视者的视力? 假设矫正镜固定在距离眼睛1.50厘米的地方。
策略
你希望这个近视的人能够清楚地看到远处的物体,这意味着眼镜镜头必须为无限远处的物体生成距离眼睛30.0厘米的图像。 距离眼睛 30.0 厘米的图像距离眼镜镜片 30.0 cm−1.50 cm=28.5 cm。 因此,当 d o = 时,我们必须有 d i =−28.5cm\(\infty\)。 图像距离为负,因为它与物体位于眼镜镜头的同一侧。
解决方案
由于 d i 和 dodo 是已知的,我们可以使用方程式\ ref {sumdiv} 来计算眼镜镜片的光功率:
\[P=\frac{1}{d_o}+\frac{1}{d_i}=\frac{1}{\infty}+\frac{1}{−0.285m}=−3.51D. \nonumber \]
意义
如预期的那样,负光功率表示发散(或凹面)透镜。 如果你检查近视者的眼镜,你会发现镜片中心最薄。 此外,如果你查看近视者的眼镜处方,你会发现规定的光功率是负的,以屈光度为单位给出。
校正远视只需使用与近视相反的镜头类型(即会聚镜头),如图所示\(\PageIndex{5}\)。
这样的镜头将生成比近点更近的物理物体的图像,该图像位于近点和远点之间的距离,这样人就可以清楚地看到图像。 因此,要确定校正所需的光功率,您必须知道该人的近点,如示例中所述\(\PageIndex{4}\)。
眼镜镜片需要多大的光学功率才能让近点为 1.00 m 的有远见的人清楚地看到距离眼睛 25.0 厘米的物体? 假设矫正镜固定在距离眼睛 1.5 cm 的地方。
策略
当物体距离人的眼睛 25.0 厘米时,眼镜镜片必须在 1.00 m 处(近点)生成图像,这样人才能清楚地看到它。 距离眼睛 1.00 米的图像将距离眼镜镜片 100cm−1.5cm=98.5 厘米,因为眼镜镜片距离眼睛 1.5 厘米。 因此,d i =−98.5cm,其中减号表示图像与物体位于镜头的同一侧。 物体距离眼镜镜片 25.0cm−1.5cm=23.5 厘米,所以 d o =23.5 厘米。
解决方案
既然 d i 和 dodo 是已知的,我们可以使用方程式\ ref {sumlens} 来计算眼镜镜片的光功率:
\[P=\frac{1}{d_o}+\frac{1}{d_i}=\frac{1}{0.285m}+\frac{1}{-0.985m}=+3.24D. \nonumber \]
意义
如预期的那样,正光功率表示会聚(凸面)透镜。 如果你检查有远见的人的眼镜,你会发现镜片中心最厚。 此外,有远见的人的处方眼镜具有正的规定光功率。


