2.5: 超薄镜头

学习目标

在本节结束时，您将能够：

• 使用射线图来定位和描述 镜头形成的图像
• 使用薄镜头方程来描述和定位镜头 形成的图像

镜头存在于大量的光学仪器中， 从简单的放大镜到相机的变焦镜头再到眼睛 本身。 在本节中，我们将使用斯内尔定律来探索镜头 的特性以及它们如何形成图像。

“镜头” 一词源自拉丁语中的扁豆一词， 其形状类似于凸透镜。 但是，并非所有 镜片的形状都相同。 \(\PageIndex{1}\)该图显示了 各种不同的镜头形状。 用来描述 镜头的词汇与用于球面反射镜的词汇相同：镜头的 对称轴称为光轴，其中与镜头表面 相交的轴称为镜头的顶点，依此类 推。

图\(\PageIndex{1}\)：各种类型的镜片： 请注意，会聚镜片的 “腰围” 较厚，而发散 镜片的腰部较薄。

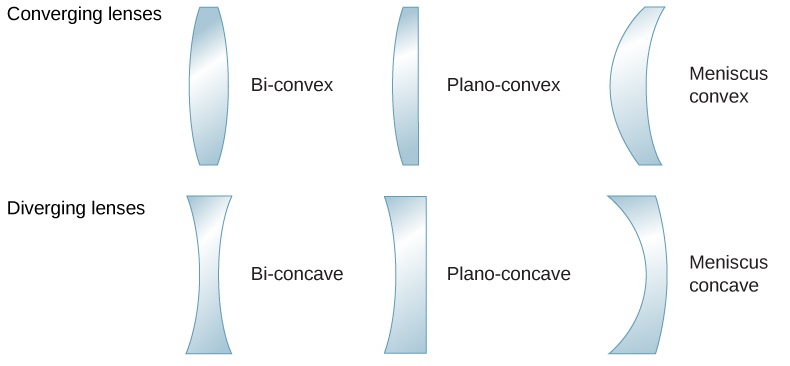
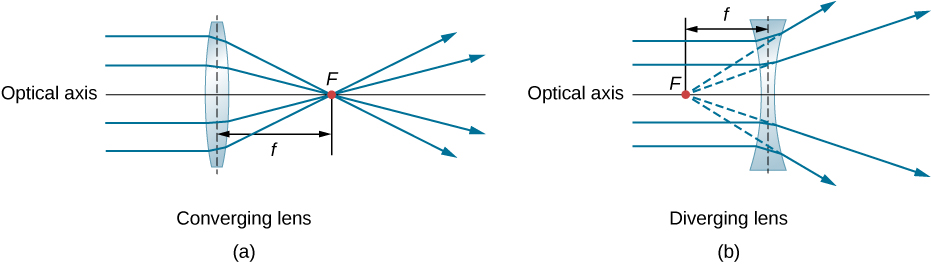
凸透镜或会聚透镜的形状使得平行于其光轴进入 该镜头的所有光线在 镜头另一侧的光轴上的单个点相交（或聚焦），如图所示\(\PageIndex{1a}\)。 同样，凹透镜或 发散透镜的形状使平行于 其光轴进入该透镜的所有光线都发散，如 (b) 部分所示。 要更 精确地了解镜头是如何操纵光线 的，请仔细观察穿过会聚镜头的顶部光线（a）。 由于镜头的 折射率大于空气的折射率， 斯内尔定律告诉我们，光线在进入镜头时会 向垂直于界面弯曲。 同样，当光线 离开镜头时，它会弯曲远离垂直线。 同样 的理由也适用于发散镜头，如图所示 \(\PageIndex{1b}\)。 总体效果是，对于会聚镜头，光线 向光轴弯曲，而对于发散镜头， 光线向光轴弯曲。 对于会聚镜头，光线穿过的 点是镜头的焦点 F。 对于发散镜头，光线似乎 起源的点是（虚拟）焦点。 从镜头 中心到焦点的距离是镜头的焦距 f。

图\(\PageIndex{2}\)：进入 (a) 会 聚镜头和 (b) 发散镜头的光线在其焦点处会 聚 F. 从 镜头中心到焦点的距离是镜头的焦距 f。请注意， 光线在进入和离开时会弯曲镜头， 总体效果是将光线向光 轴弯曲。

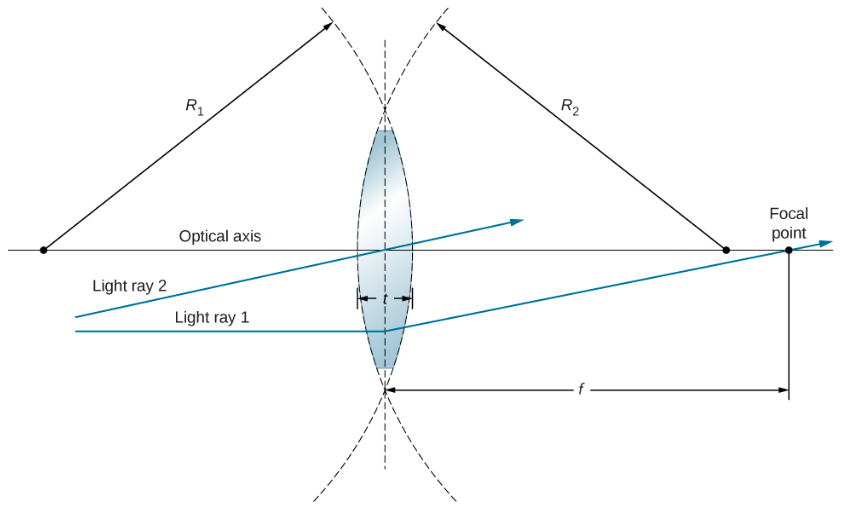
如果镜片的厚度 t 远小于两个表面的曲率半径，则该透镜被认为是薄的，如 图所示\(\PageIndex{3}\)。 在这种情况下，可以认为 光线在镜头中心弯曲一次。 对于 图中绘制的案例，光线 1 平行于光轴，因此 出射光线在镜头中心弯曲一次，然后 穿过焦点。 薄 镜片的另一个重要特征是，穿过镜头中心的光线 没有偏差，如光线 2 所示。

图\(\PageIndex{3}\)：在薄透镜 近似值中，透镜的厚度 t 远小于 镜头 表面曲率的半径 R ₁ 和 R ₂。 光线被视为在镜头 中心弯曲，例如光线 1。 光线 2 穿过 镜头中心，在薄镜头 近似值中保持不偏离。

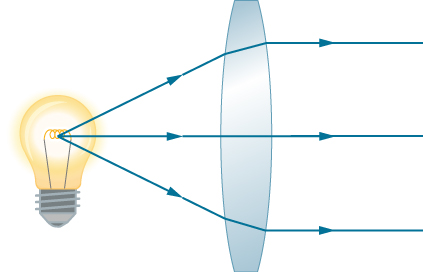
正如在对斯内尔定律的初步讨论中所指出的那样， 光线的路径是完全可逆的。 这意味着图中所有光线的箭头方向可以反转 \(\PageIndex{2}\)。 例如，如果将点光源放置 在凸透镜的焦点上，如图所示 \(\PageIndex{4}\)，平行光线会从另一 侧出现。

图\(\PageIndex{4}\)为会聚和发散 镜头。 这种技术用于灯塔，有时也用于 交通信号灯，用于从向各个方向发射光的光源 产生定向光束。

光线追踪和超薄镜头

光线追踪是一种确定或 跟踪（追踪）光线所走路径的技术。 薄透镜的光线追踪与我们在球面 反射镜中使用的技术非常相似。 至于镜子，光线追踪可以准确地描述镜头的 操作。 薄透镜的光线追踪规则与球面镜的射线追踪规则 相似：

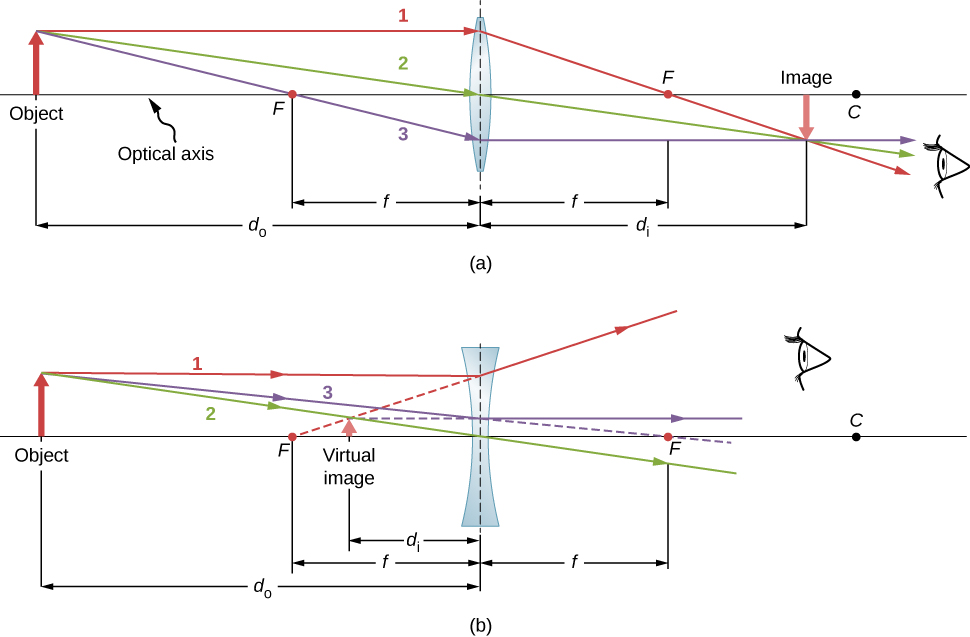
1. 进入平行于光轴的会聚镜头的光线 穿过镜头另一侧的焦点（图（a）部分 中的射线 1\(\PageIndex{4}\)）。 进入平行 于光轴的发散透镜的光线 沿着穿过镜头同一侧焦点的 线发出（图（b）部分中的射线 1）。
2. 穿过会聚或 发散透镜中心的射线不会偏离（射线 2 分为 (a) 和 (b) 部分）。
3. 对于会聚镜头，穿过焦 点的光线平行于光轴离开镜头（第 (a) 部分 为射线 3）。 对于发散镜头，沿着穿过另一侧焦点的直线 接近的射线平行于轴线离开 镜头（第 (b) 部分为射线 3）。

图\(\PageIndex{5}\)：薄镜头两侧的 焦距相同。 (a) 平行光线从 左侧焦点的右十字架进入会 聚镜头。 (b) 从 右侧进入发散镜头的平行光线似乎来自右侧的焦点。

薄镜片非常适合单色光（即单波长的光 ）。 但是，对于包含多个 波长的光（例如白光），镜头效果不佳。 问题在于，正如我们在上一章中所学到的那样，材料 的折射率取决于光的波长。 这种现象造成了许多丰富多彩的效果，例如彩 虹。 不幸的是，这种现象还会导致镜头形成的图像出现像差 。 特别是，由于镜头的焦 距取决于折射率，因此也 取决于入射光的波长。 这意味着不同波长的 光将聚焦在不同的点， 从而产生所谓的 “色差”。 特别是，白色物体图像的边缘会变 色和模糊。 称为 doublets 的特殊镜头 能够校正色差。 双光透镜是通过将会聚透镜和发散透镜 粘合在一起而形成的。 组合的双波透镜可显著减少色 差。

通过薄镜头形成图像

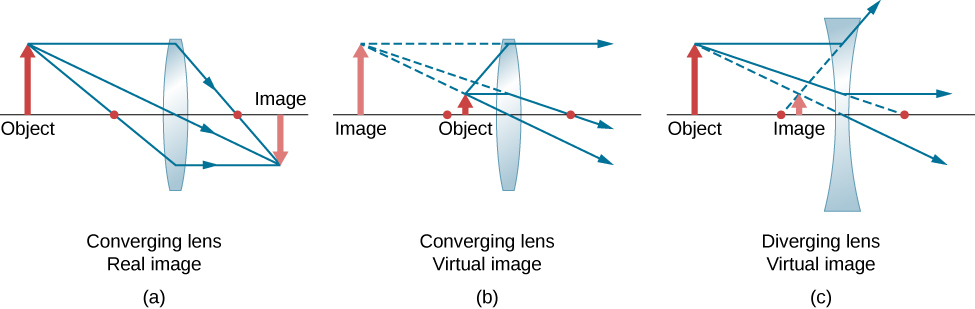
我们使用光线追踪来研究镜头 可以创建的不同类型的图像。 在某些情况下，镜头会形成 真实图像，例如当电影放映机将图像投射到 屏幕上时。 在其他情况下，图像是虚拟图像， 无法投影到屏幕上。 例如，眼镜形 成的图像在哪里？ 我们对薄镜头使用光线追踪来说明 它们是如何形成图像的，然后我们开发方程来 定量分析薄镜片的特性。

假设物体距离会聚镜头有一段距离，如图 所示\(\PageIndex{6}\)。 为了找到图像的 位置和大小，我们追踪了 从物体上一个点（在本例中为箭头）发出的选定光线的路径。 该图显示了来自箭头 尖端发出的多条射线的三条射线。 可以使用上面给出的光线追踪规则来 追踪这三条射线。

• 射线 1 平行于光轴进入镜头并 穿过另一侧的焦点（规则 1）。
• 射线 2 穿过镜头中心且不偏离 （规则 2）。
• 射线 3 在前往镜头的途中穿过焦点，并平行于光轴 离开镜头（规则 3）。

三条光线在镜头另一侧的 单点交叉。 因此，箭头尖的图像位于 此点。 所有来自箭头尖端并进入 镜头的光线都会在所示点折射并交叉。

找到箭头尖的图像后，我们需要图像的 另一个点来定向箭头的整个图像。 我们选择定位箭头的图像底座，它位于 光轴上。 正如球面反射镜部分中所解释的那样， 底座将位于光轴上，正好位于箭头尖图像 的正上方（由于镜头的上下对称性）。 因此， 图像跨越光轴到所示的（负）高度。 来自箭头上另一个点（例如箭头中间）的光线在另一个公共点 交叉，从而填充了 图像的其余部分。

尽管在此图中追踪了三条光线，但定位图像的某一点只 需要两条光线。 最好追踪有简单光线 追踪规则的射线。

图\(\PageIndex{6}\)：光线追踪用于定位 镜头形成的图像。 对来自物体上同一点 的光线进行追踪——所选的三条射线各遵循光线追踪 规则之一，因此它们的路径很容易确定。 图像位于光线交叉处。 在这种 情况下， 形成了真实的图像，即可以投影在屏幕上的图像。

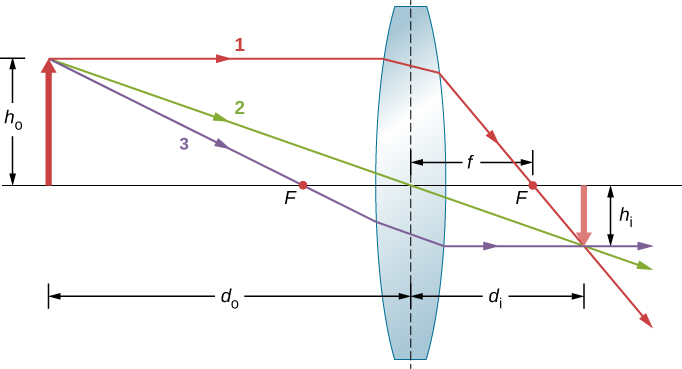
图中出现了几个重要的距离。 至于 镜子，我们将渡渡鸟定义为物体距离，或 物体与镜头中心的距离。 图像距离 d _i 被定义为图像与镜头 中心的距离。 物体的高度和 图像的高度 分别由 h _o 和 h _i 表示。 相对于物体直立的图像 具有正高度，而倒置的图像具有负 高度。 通过使用光线追踪规则并用纸和铅笔 绘制比例图，如图所示 \(\PageIndex{6}\)，我们可以准确地描述图像 的位置和大小。 但是光线追踪的真正好处在于可视化图像在各种情况下是 如何形成的。

斜平行光线和焦平面

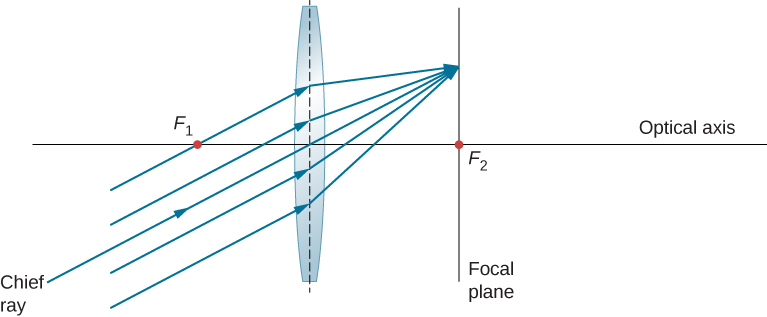
我们已经看到，平行于光轴的光线被引导 到会聚镜头的焦点。 在发散 镜头的情况下，它们朝着一个方向发出，使它们看起来像 来自镜头另一侧（即平行光线进入镜头的那一侧）的焦点。 不 平行于光轴的平行光线会怎样（图 \(\PageIndex{7}\)）？ 在会聚镜头的情况下，这些光线 不会在焦点处会聚。 相反，它们聚集在飞机上的 另一个点上，称为焦平面。 焦平面 包含焦点，垂直于光轴。 如图所示，平行光线聚焦在穿过镜头中心的光线穿过焦平面的位置。

图\(\PageIndex{7}\)：平行斜光线聚焦在焦平面中的一个点 上。

薄透镜方程

光线追踪使我们能够获得图像 形成的定性图片。 为了获得数值信息，我们从薄透镜光线追踪的几何分析中得出一对 方程。 这些方程称为薄透镜方程和镜头制造商 方程，使我们能够定量分析薄透镜。

以图中所示的厚双凸透镜为例 \(\PageIndex{8}\)。 周围 介质的折射率为 n ₁（如果镜头在空气中，则为\(n_1=1.00\)） ，镜头的折射率为 n 1\(n_2\)。 两 边的曲率半径为\(R_1\)和\(R_2\)。 我们希望找到物体距离\(d_o\)、图像距离\(d_i\)和镜头 参数之间的 关系。

该图\(\PageIndex{8}\)用于推导镜头制造商 的方程式。 这里\(t\)是镜头的厚度，n ₁ 是 外部介质的折射率，\(n_2\)是镜头的 折射率。 我们利用极限\(t→0\) 得出薄镜头的公式。

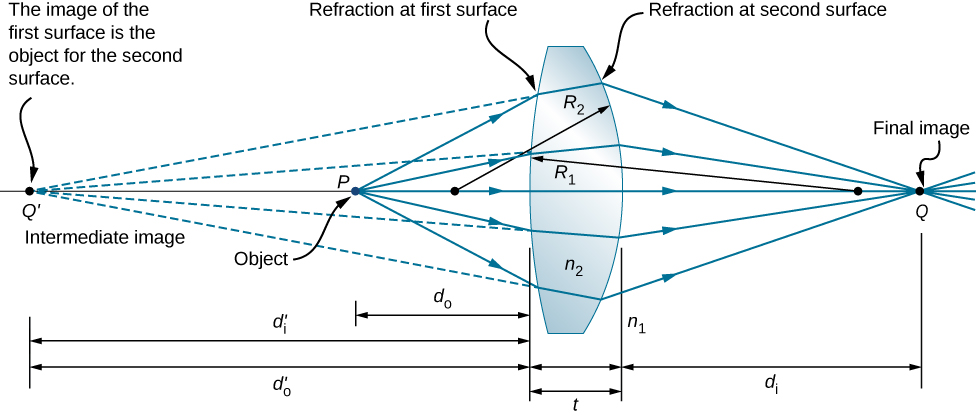
为了得出薄透镜方程，我们考虑 由第一个折射表面（即左表面）形成的图像，然后使用 该图像作为第二个折射表面的对象。 在 图中，来自第一个折射表面的图像是\(Q′\) ，它是通过将 镜头内部的光线向后延伸而形成的（这些光线是由第一个表面的折射产生的）。 如图 中的虚线所示。 请注意，这张图像 是虚拟的，因为实际上没有光线穿过点 Q′。 为了 找到与图像 Q′\(d′_i\) 相对应的图像距离，我们 使用方程 2.4.9。 在这种情况下，物体距离为\(d_o\)，图像距离为 d'idi′，曲率半径为\(R_1\)。 将它们 插入先前为曲线表面折射而生成的 关系中 可以得出

\ [\ dfrac {n_1} {d_o} +\ dfrac {n_2} {d′ _i} =\ dfrac {n_2−n_1} {R_1}。 \ label {51}\]

图像是虚拟的，与物体在同一边，所以 d _i '<0 和 d _o >0。 第一个表面朝向物体 凸起，所以\(R_1>0\)。

要找到由第二个界面 折射\(Q\)形成的物体的物体距离，请注意，在方程式 2.4.9 中，折射率 n ₁ 和 n ₂ 的作用是 互换的。 在图中\(\PageIndex{8}\)，光线起源于具有 索引的介质\(n_2\)，而在 图 2.4.3 中，光线起源于具有索引的介质 \(n_1\)。 因此，我们必须 在方程 2.4.9 中互换 n ₁ 和 n ₂。 此外，通过再次查看 Figure\(\PageIndex{8}\) ，我们可以看到物体距离为\(d′_o\)，图像距离为 \(d_i\)。 曲率半径为 R ₂ 将这些 量插入方程 2.4.9 可以得出

\ [\ dfrac {n_2} {d'_o} +\ dfrac {n_1} {d_i} =\ dfrac {n_1−n_2} {R_2}。 \ label {eq51}\]

图像是真实的，与物体在相反的一侧，所以 \(d_i>0\)和\(d_o′>0\)。 第二个表面是凸起的，远 离物体，所以\(R_2<0\)。 方程\ ref {eq51} 可以通过注意以下几点来 简化

\[d′_o=|d′_i|+t, \nonumber \]

其中，我们取绝对值是因为\(d′_i\)是 负数，而\(d′_o\)和\(t\)都是正数。 如果我们否定绝对值， 我们可以省略绝对值\(d′_i\)，这 给出了

\[ d′_o=−d′_i+td. \nonumber \]

将其插入方程式\ ref {eq51} 可以得出

\ [\ dfrac {n_2} {−d'_i+t} +\ dfrac {n_1} {d_i} =\ dfrac {n_1−n_2} {R_2}。 \ label {eq52}\]

求和方程\ ref {eq51} 和\ ref {eq52} 给出

\ [\ dfrac {n_1} {d_o} +\ dfrac {n_1} {d_i} +\ dfrac {n_2} {d^_i} +\ dfrac {n_2} {−d^_i+t} = (n_2−n_1) \ 左 (\ dfrac {1} {R_1} c {1} {R_2}\ 右）。 \ label {eq54}\]

在 薄镜头近似值中，我们假设镜头与第一个图像距离或\(t \ll d′_i\)（或 等效地为 and\(t \ll R_2\)）相比非常薄。\(t \ll R_1\) 在这种情况下，方程\ ref {eq54} 左侧的 第三和第四项被 取消，剩下的是

\ [\ dfrac {n_1} {d_o} +\ dfrac {n_1} {d_i} = (n_2−n_1) \ 左 (\ dfrac {1} {R_1} −\ dfrac {1} {R_2}\ 右)。 \ nonnumber\]

除以终于\(n_1\)给我们了

\ [\ dfrac {1} {d_o} +\ dfrac {1} {d_i} =\ 左 (\ dfrac {n_2} {n_1} −1 \ 右)\ 左 (\ dfrac {1} {R_2}\ 右)。 \ label {eq58}\]

左侧看起来像我们在上面得出的球 面反射镜的镜像方程式一样令人怀疑。 与球面镜 一样，我们可以使用光线追踪和几何图形来 表明，对于薄透镜，

\ [ \ underbrace {\ dfrac {1} {d_o} +\ dfrac {1} {d_i} =\ dfrac {1} {f}} _ { \ text {薄镜头方程}}\ label {薄镜头方程}\]

哪里\(f\)是薄镜头的焦距（这个 推导留作练习）。 这是薄镜头 方程。 薄镜头的焦距与镜头 左侧和右侧的焦距相同。 组合方程 \ ref {薄镜头方程} 和\ ref {eq58} 可以得出

\ [\ underbrace {\ dfrac {1} {f} =\ 左 (\ dfrac {n_2} {n_1} −1 \ 右)\ 左 (\ dfrac {1} {R_1} {R_2}\ 右)} _ {\ text {镜头制造商 的方程式}\ label {lensmaker}\]

这被称为镜头制造商的方程式。 它 表明，薄镜头的焦距仅取决于镜头和 周围介质的 曲率半径和折射率。 对于空中的镜头\(n_1=1.0\)\(n_2≡n\)， 所以镜头制造商的方程式简化为

\ [\ dfrac {1} {f} = (n−1) \ 左 (\ dfrac {1} {R_1} −\ dfrac {1} {R_2}\ 右)。 \ nonnumber\]

镜头的签名惯例

要正确使用薄透镜方程，必须遵守以下符号 惯例：

• \(d_i\)如果图像位于 物体对面的一侧（即真实图像），则为正值；否则，\(d_i\)为负数（即 虚拟图像）。
• \(f\)对于会聚透镜为正，对于 发散透镜为负。
• \(R\)对于向物体凸起的表面，为正值；对于朝向物体凹面的表面，为 负值。

放大倍率

通过在光轴上使用有限尺寸的物体和光线 追踪，可以证明图像\(m\)的放大倍率 为

\[m \equiv \dfrac{h_i}{h_o}=−\dfrac{d_i}{d_o} \label{mag} \]

（其中三行表示 “定义为”）。 这与我们获得 的反射镜方程完全相同（参见方程 2.3.15）。 如果\(m>0\)，则图像与物体具有相同的垂直 方向（称为 “直立” 图像）。 如果 m<0， 则图像的垂直方向与物体相反 （称为 “倒置” 图像）。

使用薄镜头方程

薄镜头方程和镜头制造商方程广泛 适用于涉及薄镜片的情况。 我们在以下示例中探讨了图像形成的许多 特征。

以薄的聚合镜头为例。 当物体从 无限远接近镜头时，图像在哪里形成以及形成 什么类型的图像？ 这可以通过使用 给定焦距的薄镜头方程将图像距离绘制为 物体距离的函数来看出。 换句话说，我们绘制

\[d_i=\left(\dfrac{1}{f}−\dfrac{1}{d_o}\right)^{−1} \nonumber \]

给定值为\(f\)。 对于\(f=1\,cm\)，结果如图 所示\(\PageIndex{9a}\)。

图\(\PageIndex{9}\)：(a) 薄型会 聚镜头的图像距离，其中 f=1.0 cm 是物体距离的函数。 (b) 同样的但用于 f=−1.0 cm 的发散透镜。

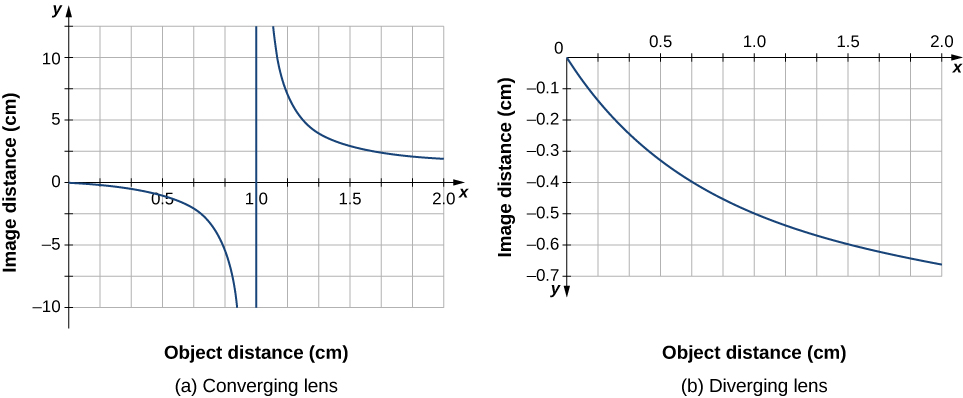
距离 镜头焦距 f 远的物体应该在焦平面附近生成图像，因为与第一个项相比，上面方程右侧的 第二个项 可以忽略不计，所以我们有\(d_i≈f\)。 这 可以从图 (a) 部分的图中看出，该图显示 ，对于较大的物体距离，图像距离渐近接近 1 cm 的焦距。 当物体接近焦 平面时，图像距离会发散到正无穷大。 这是 预料之中的，因为焦平面上的物体会产生平行 光线，这些光线在无穷大（即离镜头很远）处形成图像。 当物体距离镜头的焦距远时， 图像距离为正，因此图像是真实的，位于镜头与物体的对 面，并且是反向的（因为 \(m=−d_i/d_o\)通过方程式\ ref {mag}）。 当物体距离镜头的焦距 更近时，图像距离变为 负值，这意味着图像是虚拟的，与物体位于镜头 的同一侧，并且是直立的。

对于焦距较薄的发散镜头\(f =−1.0\, cm\)，图中显示了 相似的图像距离与物体距离的关系 图\(\PageIndex{10b}\)。 在这种情况下，所有正物体距离的图像距离均为 负数，这意味着 图像是虚拟的，与物体位于镜头的同一侧，并且是 直立的。 这些特征也可以通过光线追踪 图（图\(\PageIndex{10}\)）看出。

图\(\PageIndex{10}\)：红点表示镜头的焦 点。 (a) 由距离会聚 镜头焦距更远的 物体形成的真实倒置图像。 (b) 由距离镜头焦距 更近的物体形成的虚拟、直立图像。 (c) 由距离发散镜头焦距 远的物体形成的虚拟、直立 图像。

要查看直立和倒置图像的具体示例，请 看图\(\PageIndex{11}\)，它显示了当物体（本例中为人的脸） 放置在与镜头不同距离时由镜头会 聚形成的图像。 在 图的（a）部分中，人脸距离 镜头的焦距超过一个焦距，因此图像是反向的。 在 (b) 部分中，人脸距离镜头的焦距比一个焦距 更近，因此图像是 直立的。

图\(\PageIndex{11}\)：(a) 当聚焦镜头 距离男人的脸部超过一个焦距时，会形成 倒置图像。 请注意，图像处于对焦状态，但 脸部未对焦，因为图像比脸部更接近拍摄 这张照片的相机。 (b) 当聚合镜头距离其 脸部不到一个 焦距时，便会生成直立的脸部图像。 （来源 a：修改 “DamonGMan” /Flickr 的作品；来源 b：Casey Fleser 对作品的修改）

仔细阅读以下示例，以更好地了解 薄镜片的工作原理。

问题解决策略：镜头

• 第 1 步。 确定光线追踪、薄透镜方程 或两者兼而有用。 即使不使用光线追踪，仔细的 草图也总是非常有用的。 在 草图上写下符号和值。
• 第 2 步。 确定问题中需要确定的内容 （找出未知数）。
• 第 3 步。 列出给出或可以从 问题中推断出的内容（找出已知因素）。
• 第 4 步。 如果需要光线追踪，请使用本节开头附近 列出的光线追踪规则。
• 第 5 步。 大多数定量问题都需要使用 薄镜头方程和/或镜头制造商方程。 求解这些 未知数，然后插入给定数量或将两者 一起使用以找到两个未知数。
• 第 7 步。 检查答案是否合理。 这些迹象 是否正确？ 草图或光线追踪与 计算结果一致吗？

示例\(\PageIndex{1}\)：使用镜头 制造商方程

找出由折射率为1.55的玻璃对称 研磨的双凹透镜的曲率半径，使其在空气中的焦 距为20 cm（对于双凹透镜，两个表面的曲率半径相同）。

策略

使用镜头制造商方程式的薄镜片形式：

\ [\ dfrac {1} {f} =\ 左 (\ dfrac {n_2} {n_1} −1\ 右)\ 左 (\ dfrac {1} {R_1}\ 右) \ nonumber\]

在哪里\(R_1<0\)和\(R_2>0\)。 因为我们正在制作对 称的双凹透镜，所以我们有\(|R_1|=|R_2|\)。

解决方案

我们可以通过以下公式确定曲率半径\(R\)

\ [\ dfrac {1} {f} = \ 左 (\ dfrac {n_2} {n_1} −1\ 右)\ 左 (\ dfrac {−2} {R}\ 右)。 \ nonnumber\]

求解\(R\)并插入\(f=−20\,cm\)\(n_2=1.55\)，然后 \(n_1=1.00\)给出

\ [\ begin {align} R &=−2f\ 左 (\ dfrac {n_2} {n_1} −1\ 右) \ nonumber\\ [4pt] &=−2 (−20\, cm) \ 左 (\ dfrac {1.55} {1.00} −1\ 右)\ non数字\\ [4pt] &= 22\, cm。 \ nonumber\ end {align}\ nonumber\]

示例\(\PageIndex{2}\)：聚合镜头和 不同的物体距离

在焦距为 10.0 cm 的凸透镜 前面的以下每个位置找出 3.0 cm 高的物体的图像 位置、方向和放大倍率。 (a) \(d_o=50.0\,cm\)、(b)\(d_o=5.00\,cm\) 和 (c)\ (d_o=20.0\, cm\)。

策略

我们从薄透镜方程（方程\ ref {薄透镜 方程}）开始

\[\dfrac{1}{d_i}+\dfrac{1}{d_o}=\dfrac{1}{f}. \nonumber \]

为图像距离求解这个问题\(d_i\)并插入给定的 物体距离和焦距。

解决方案

a. 对于\(d_o=50\, cm\) and\(f=+10\, cm\)，这给了

\ [\ begin {align} d_i &= \ 左 (\ dfrac {1} {f} −\ dfrac {1} {d_o}\ 右) ^ {−1}\ nonumber\\ [4pt] &=\ 左 (\ dfrac {1} {10.0\, cm} −\ dfrac {1} {50.0cm}\ 右) {^ −1}\ nonumber \\ [4pt] &=12.5\, cm\ nonumber\ end {align} \ nonumber\]

图像是正面的，因此图像是真实的，位于镜头与物体的对 面，距离镜头12.6厘米。 要 找到图像的放大倍率和方向，请使用

\ [\ begin {align} m &=−\ dfrac {d_i} {d_o}\ nonumber\\ [4pt] &=−\ dfrac {12.5\, cm} {50.0\, cm}\ nonumber\\ [4pt] &=−0.250。 \ nonumber\ end {align}\ nonumber\]

负放大倍率意味着图像是反向的。 因为\(|m|<1\)，图像比物体小。 图像 的大小由下式给出

\ [\ begin {align} |h_i| &=|m|h_o \ nonumber\\ [4pt] & =( 0.250) (3.0\, cm)\ nonumber\\ [4pt] &=0.75\, cm\ nonumber\ end {align}\ nonumber\]

b. For an\(d_o=5.00\,cm\) d\(f=+10.0\,cm\)

\ [\ begin {align} d_i&=\ 左 (\ dfrac {1} {f} −\ dfrac {1} {d_o}\ 右) ^ {−1} \ nonumber\\ [4pt] &=\ 左 (\ dfrac {1} {5.00\, cm}\ 右) ^ {1}\ nonumber\\ [4pt] &=−10.0\, cm\ nonumber\ end {alig n}\ nonumber\]

图像距离为负，因此图像是虚拟的，与物体位于 镜头的同一侧，距离 镜头10厘米。 图像的放大倍率和方向可 从中找到

\ [\ begin {align} m &=−\ dfrac {d_i} {d_o}\ nonumber\\ [4pt] &=−\ dfrac {−10.0\, cm} {5.00\, cm}\ nonumber\\ [4pt] &=+2.00。 \ nonumber\ end {align}\ nonumber\]

正放大倍率意味着图像是直立的 （即，它与物体的方向相同）。 因为 \(|m|>0\)，图像比物体大。 图像的大小是

\ [\ begin {align} |h_i|&=|m|h_o\ nonumber\\ [4pt] & =( 2.00) (3.0\, cm)\ nonumber\\ [4pt] &=6.0\, cm。 \ nonumber \ end {align}\ nonumber\]

c. For an\(d_o=20\,cm\) d\(f=+10cm\)

\ [\ begin {align} d_i &= \ 左 (\ dfrac {1} {f} −\ dfrac {1} {d_o}\ 右) ^ {−1}\ nonumber\\ [4pt] &=\ 左 (\ dfrac {1} {20.0\, cm}\ 右) ^ {1}\ nonumber\\ [4pt] &=20.0\, cm\ nonumber\ end {align} \ nonumber\]

图像距离为正，因此图像是真实的，位于镜头与物体的 对面，距离镜 头20.0 cm。 放大倍率是

\ [\ begin {align} m &=−\ dfrac {d_i} {d_o}\ nonumber\\ [4pt] &=−\ dfrac {20.0\, cm} {20.0\, cm}\ nonumber\\ [4pt] &=−1.00。 \ nonumber\ end {align}\ nonumber\]

负放大倍率意味着图像是反向的。 因为\(|m|=1\)，图像与物体的大小相同。

在解决几何光学问题时，我们经常需要 将光线追踪和镜头方程相结合。 以下示例 演示了这种方法。

示例\(\PageIndex{3}\)：选择镜头的焦 距和类型

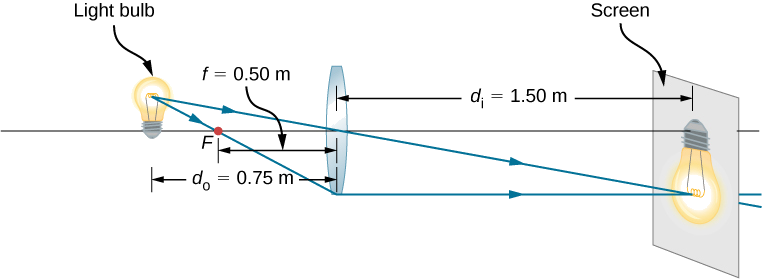
要将灯泡的图像投射到 1.50 米外的屏幕上， 您需要选择要使用的镜头类型（会聚或发散） 及其焦距（图\(\PageIndex{12}\)）。 镜头和灯泡 之间的距离固定为 0.75 m。另外，图像的放大倍率和方向 是多少？

图\(\PageIndex{12}\)：放置在 距离焦距为 0.50 米的镜头 0.75 米处的灯泡会在 屏幕上生成真实图像，如示例中所述。 光线追踪可预测图像的 位置和大小。

策略

图像必须是真实的，所以你选择使用会聚镜头。 焦距可以通过使用薄镜头方程并 求解焦距来找到。 物体距离为 \(d_o=0.75\,m\)，图像距离为\(d_i=1.5\,m\)。

解决方案

求解薄镜头的焦距，然后插入所需的 物体和图像距离：

\ [\ begin {alig n}\ dfrac {1} {d_o} +\ dfrac {1} {d_i} &=\ dfrac {1} {f}\ nonumber\\ [4pt] f &=\ 左 (\ dfrac {1} {d_i}\ 右) ^ {−1}\ nonumber \\ [4pt] &=\ 左 ( \ dfrac {1} {0.75\, m} +\ dfrac {1} {1.5\, m}\ 右) ^ {−1}\ nonumber \\[4pt] &= 0.50 \, m \nonumber \end{align} \nonumber \]

放大倍率是

\ [\ begin {align} m &=−\ dfrac {d_i} {d_o}\ nonumber\\ [4pt] &= −\ dfrac {1.5\, m} {0.75\, m}\ nonumber\\ [4pt] &=−2.0。 \ nonumber \ end {align}\ nonumber\]

意义

放大倍率的减号表示图像是 反向的。 正如 聚光镜头所预期的那样，焦距为正。 光线追踪可用于检查计算结果 （图\(\PageIndex{12}\)）。 不出所料，图像是反向的，是 真实的，并且比物体大。