2.4: 由折射形成的图像

Last updated

Nov 1, 2022
Page ID
202305
Save as PDF
- 2.3: 球面反射镜
- 2.5: 超薄镜头

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

在本节结束时，您将能够：

描述由单折射表面形成的图像
确定图像的位置并使用射线图计算其属性
使用单折射表面的方程确定图像的位置并计算其属性

当光线从一种介质传播到另一种介质时，这些光线会发生折射，也就是光波在两种介质之间的界面处弯曲的时候。折射表面可以以与反射表面相似的方式形成图像，唯一的不同是折射定律（斯内尔定律）是该过程的核心，而不是反射定律。

平面界面的折射——表观深度

如果你看一根部分浸入水中的直杆，它似乎在表面弯曲。这种奇怪效果背后的原因是，水中鱼竿的图像比鱼竿的实际位置更接近水面，因此它与水面上方的鱼竿部分不对齐。同样的现象解释了为什么水中的鱼看起来比实际更接近水面。

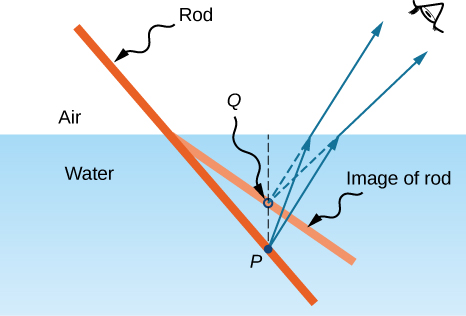
该图描绘了浸入水中的鱼竿的侧视图。标有杆图像的较浅线条的显示方式使杆看起来好像在空气和水的交界处弯曲了一样。点 P 在杆上，点 Q 在杆的图像上。虚线 PQ 显示为垂直于水面。两条光线来自 P，向上传播到水面，成一定角度弯曲并到达观察者的眼睛。弯曲光线的背部延伸似乎起源于 Q 点。 — 图 $\PageIndex{1}$ ：杆在水气接口处弯曲。杆 $P$ 上的点似乎在点上 $Q$ ，这是由于气水界面的折射而形成点P的图像的地方。

要研究折射导致的图像形成，请考虑以下问题：

当光线进入或穿过另一种介质时，它们会发生什么？
来自单点的折射光线是在某个点相遇还是彼此分散？

具体而言，我们考虑一个由平面接口分隔的两个介质组成的简单系统（图 $\PageIndex{2}$ ）。物体在一种媒介中，观察者在另一种媒介中。例如，当你从水面上方观察一条鱼时，鱼处于中等 1（水），折射率为 1.33，你的眼睛处于中等 2（空气），折射率为 1.00，水面是界面。你 “看见” 的深度是图像高度 $h_i$ ，称为表观深度。鱼的实际深度是物体的高度 $h_o$ 。

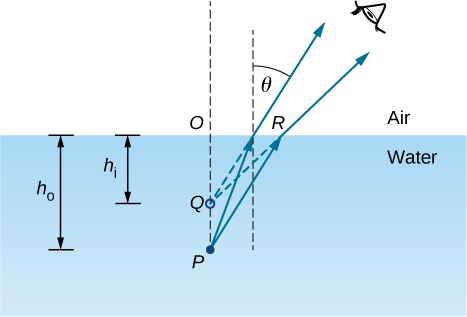
该图显示了一定量水的侧视图。 P 点位于其中。两条光线来自点 P，在水面弯曲并到达观察者的眼睛。这些折射光线的背部延伸在 Q 点相交。PQ 垂直于水面，在 O 点与水面相交。Distance OP 标记为 h 下标 o，距离 OQ 标记为 h 下标 i。折射光线形成的角度，直线垂直于水面被标记为 theta。 — 图 $\PageIndex{2}$ ：折射产生的表观深度。 P 点处的真实物体在 Q 点创建图像。图像的深度与物体的深度不同，因此观察者以 “表观深度” 看到图像。

视在深度 h _i 取决于您查看图像的角度。对于从上方看的视图（所谓的 “正常” 视图），我们可以将折射角近似 $θ$ 得很小，并在斯内尔定律 $\sin θ$ 中替换为 $\tan θ$ 。有了这个近似值，你可以使用三角形 $ΔOPR$ $ΔOQR$ 来表明表观深度由下式给出

$h_i= \left(\dfrac{n_2}{n_1}\right)h_o. \nonumber$

这个结果的推导留作练习。因此，从上方观察时，鱼出现在实际深度的3/4处。

球形界面处的折射

球形在光学中起着重要作用，主要是因为高质量的球形比其他曲面更容易制造。为了研究单个球面上的折射，我们假设一端为球形表面的介质无限延续（“半无限” 介质）。

凸面折射

假设一个点光源位于由玻璃制成的凸面前的 P 点（图 $\PageIndex{3}$ ）。假 $R$ 设曲率半径，n ₁ 是物点 P 所在介质的折射率，n ₂ 是具有球形表面的介质的折射率。我们想知道这个界面上的折射会发生什么。

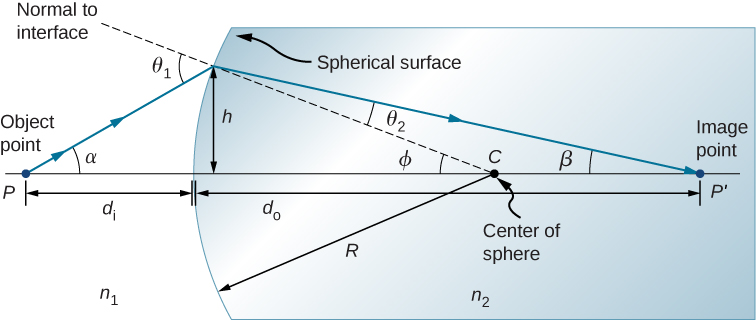
该图显示了球体的一部分。空气的折射率为 n 下标 1，球体的折射率为 n 下标 2。球体的中心为 C，半径为 R。源自球体外光轴上点 P 的射线撞击球体的凸面并在其内折射。它在球体内的 P prime 点处与轴相交，位于中心的另一侧。标有 “垂直于界面” 的虚线将球体中心连接到入射点。它与光轴形成一个角度 phi。入射光线和折射光线分别形成角度 alpha 和 beta，光轴和角度 theta 1 和 theta 2 分别与界面垂直。 — 图 $\PageIndex{3}$ ：凸面折射（ $n_2>n_1$ ）。

由于所涉及的对称性，仅检查一个平面中的射线就足够了。该图显示了一条光线，该光线从物体点开始 $P$ ，在界面折射，然后穿过图像点 $P′$ 。我们得出一个与物体距离 $d_o$ 、图像距离 $d_i$ 和曲率半径相关的公式 $R$ 。

将斯内尔定律应用于从点发出的射线 $P$ 可以得出

$n_1\sin θ_1=n_2 \sin θ_2. \nonumber$

在小角度近似值内

$\sin θ≈θ, \nonumber$

然后，斯内尔定律采取了形式

$n_1θ_1≈n_2θ_2. \label{eq8}$

从图的几何图 $\PageIndex{3}$ 形中我们可以看出

$θ_1=α+ϕ, \nonumber$

$θ_2=ϕ−β. \nonumber$

将两个表达式插入方程\ ref {eq8} 可以得出

$n_1(α+ϕ)≈n_2(ϕ−β). \label{eq10}$

使用图 $\PageIndex{3}$ ，我们计算角度的正切值 $α$ $β$ 、和 $ϕ$ ：

$\tan α≈\dfrac{h}{d_o}$
$\tan β≈\dfrac{h}{d_i}$
$\tan ϕ≈\dfrac{h}{R}$

再次使用小角度近似值，我们发现了这一点 $\tan θ≈ θ$ ，所以上述关系变成了

$α≈\dfrac{h}{d_o}$
$~β≈\dfrac{h}{d_i}$
$~ϕ≈\dfrac{h}{R}.$

将这些角度放入方程式\ ref {eq10} 可以得出

$n_1\left(\dfrac{h}{d_o}+\dfrac{h}{R}\right)=n_2 \left(\dfrac{h}{R}−\dfrac{h}{d_i}\right). \nonumber$

我们可以更方便地把这个写成

$\dfrac{n_1}{d_o}+\dfrac{n_2}{d_i}=\dfrac{n_2−n_1}{R}. \label{eq20}$

如果将物体放置在称为第一个焦点或物体焦点的特殊点上 $F_1$ ，则图像将在无穷大处形成，如图所示 $\PageIndex{4a}$ 。

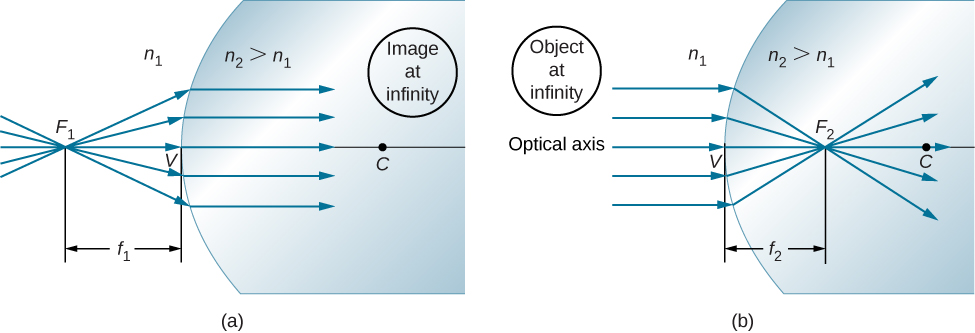
图 a 显示了球体的一部分及其外部光轴上的 F1 点。源自 F1 的光线撞击凸面并在球体内作为平行射线折射。 F1 与表面的距离为 f 下标 1。图 b 显示平行于光轴的光线撞击凸面并被折射。它们在球体内的 F2 点处会聚。 F2 位于表面和球体中心之间的光轴上。 F2 与表面的距离为 f 下标 2。在这两个图中，空气的折射率均为 n1，球体的折射率为 n2 大于 n1。 — 图 $\PageIndex{4}$ ：(a) 凸面折射的第一个焦点（称为 “物体焦点”）。 (b) 第二个焦点（称为 “图像焦点”），用于在凸面处进行折射。

我们可以 $F_1$ 通过在方程式\ ref {eq20} $d_i=\infty$ 中设置来找到第一个焦点的位置 $f_1$ 。

$\begin{align} \dfrac{n_1}{f_1}+\dfrac{n_2}{\infty} &=\dfrac{n_2−n_1}{R} \\[4pt] f_1 &=\dfrac{n_1R}{n_2−n_1} \end{align} \nonumber$

同样，我们可以定义第二个焦点或图像焦点， $F_2$ 其中图像是为较远的物体形成的（图 $\PageIndex{4b}$ ）。第二个焦点 $F_2$ 的位置通过设置从方程式\ ref {eq20} 中获得 $d_0=\infty$ ：

$\begin{align} \dfrac{n_1}{\infty}+\dfrac{n_2}{f_2}=\dfrac{n_2−n_1}{R} \\[4pt] f_2=\dfrac{n_2R}{n_2−n_1}. \end{align} \nonumber$

请注意，物体焦点与顶点的距离与图像焦点的距离不同，因为 $n_1≠n_2$ 。

单折射表面的符号惯例

尽管我们推导出这个方程用于凸面上的折射，但如果我们使用以下符号惯例，则同样的表达式适用于凹面：

$R>0$ 如果表面朝向物体凸起；否则， $R<0$ 。
$d_i>0$ 如果图像是真实的并且与物体的对面；否则， $d_i<0$ 。