2.3: 球面反射镜

Last updated
Save as PDF

Page ID: 202304

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

在本节结束时，您将能够：

描述球面反射镜形成的图像。
使用射线图和镜像方程来计算球面镜中图像的属性。

平面镜中的图像与物体大小相同，是直立的，镜子后面的距离与物体在镜子前面的距离相同。另一方面，曲面镜可以形成比物体大或小的图像，并且可以在镜子前面或镜子后面形成。一般来说，任何曲面都会形成图像，尽管有些图像会失真以至于无法辨认（想想有趣的房子镜子）。由于曲面反射镜可以创建如此丰富的图像，因此它们被用于许多具有多种用途的光学设备中。我们将主要关注球面反射镜，因为它们比抛物面反射镜等反射镜更容易制造，因此更常见。

曲面反射镜

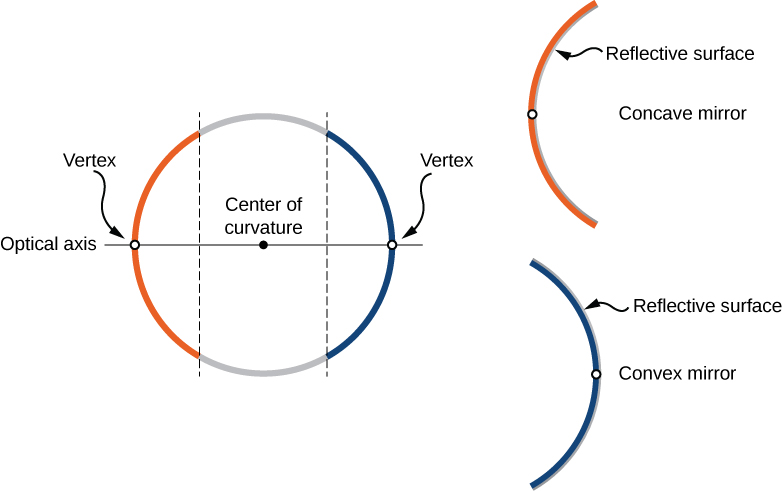
我们可以定义两种一般类型的球面反射镜。如果反射面是球体的外侧，则反射镜称为凸面镜。如果内表面是反射面，则称为凹面镜。

对称性是包括反射镜和镜头在内的许多光学器件的主要标志之一。此类光学元件的对称轴通常称为主轴或光轴。对于球面镜，光轴穿过镜子的曲率中心和镜子的顶点，如图所示\(\PageIndex{1}\)。

图 a 显示了一个圆圈，由两条平行线分开，形成两条弧线，橙色和蓝色。一条标有光轴的直线穿过圆的中心，在两条弧线的中点与圆心相交。每个中点都被标记为顶点。图 b 显示了标记为凹面镜的橙色弧线，内部显示了反射面。图 c 显示了标有凸面镜的蓝色弧线，外面显示了反射面。 — 图\(\PageIndex{1}\)。球面镜是通过切出一块球体并在内表面或外表面镀银而形成的。凹面镜的内表面有银色（比如 “洞穴”），凸面镜的外表面有银色。

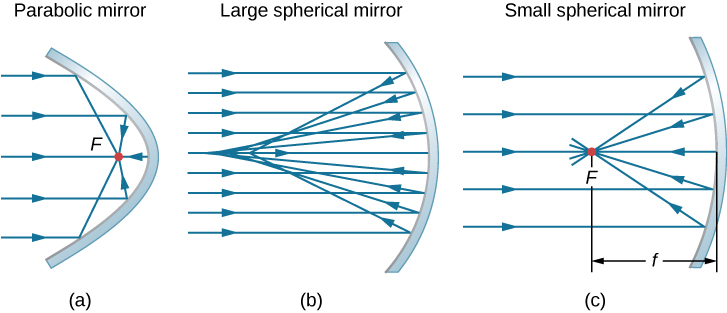
以平行于抛物线镜光轴的光线为例，如图所示\(\PageIndex{2a}\)。根据反射定律，这些光线被反射以使其在称为焦点的某个点上会聚。该图\(\PageIndex{2b}\)显示了与其曲率半径相比较大的球面镜。对于这面镜子来说，反射光线不会在同一点交叉，因此镜子没有清晰的焦点。这称为球面像差，它会导致扩展物体的图像模糊。该图\(\PageIndex{2c}\)显示了与其曲率半径相比较小的球面镜。这面镜很好地近似于抛物线反射镜，因此平行于光轴到达的光线会被反射到定义明确的焦点。沿光轴从反射镜到焦点的距离称为镜子的焦距。

图 a 显示了抛物线镜的横截面。平行光线从中反射出来，并在抛物线内标有 F 的点处汇聚。图 b 显示了从弧线反射的平行光线。它们反射到彼此靠近的各个不同点。图 c 显示了一条弧线，其曲率半径比图 b 中的弧线大得多。平行光线从中反射并在标有 F 的点处会聚。从点 F 到镜子的距离标记为 f。 — 图\(\PageIndex{2}\)：(a) 抛物面反射镜反射的平行光线在称为焦点的单点交叉 F。(b) 从大型球面镜反射的平行光线在公共点不交叉。 (c) 如果球面镜与其曲率半径相比很小，则它最好接近抛物线镜的中心部分，因此平行光线基本上在共同点交叉。沿光轴从反射镜到焦点的距离是反射镜的焦距 f。

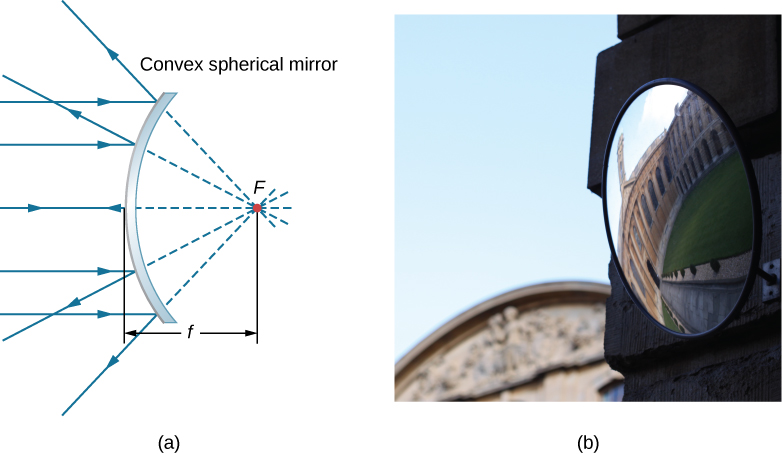
凸面球面镜也有焦点，如图所示\(\PageIndex{3}\)。平行于光轴的入射光线从反射镜反射，似乎来自反射镜\(f\)后面焦距\(F\)处的点。因此，焦点是虚拟的，因为没有真正的光线真正穿过它；它们似乎只来自它。

图 a 显示了凸面镜的横截面。平行光线从中反射并在不同的方向发散。反射光线在背面通过虚线延伸，似乎来自镜子后面的单个点。该点被标记为 F。从该点到镜子的距离标记为 f。图 b 显示了反射建筑物图像的凸面镜的照片。图像弯曲且失真。 — 图\(\PageIndex{3}\)：(a) 凸面球面镜反射的光线：平行于光轴的入射光线从凸面球面镜反射，似乎来自反射镜另一侧焦距 f 处定义明确的焦点。焦点是虚拟的，因为没有真正的光线穿过它。 (b) 由凸面镜形成的虚拟图像的照片。（来源 b：珍妮·唐宁对作品的修改）

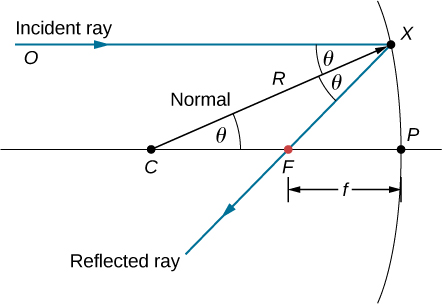
镜子的焦距与镜子的曲率半径有何关系？图中\(\PageIndex{4}\)显示了由球面凹面反射镜反射的单条射线。入射光线平行于光轴。反射光线穿过光轴的点是焦点。请注意，所有平行于光轴的入射光线都会通过焦点反射——为简单起见，我们只显示一条光线。我们想知道焦距\(FP\)（用表示\(f\)）与镜子的曲率半径有何关系\(R\)，镜子的长度为

\[R=CF+FP. \label{eq31} \]

反射定律告诉我们角度\(\angle OXC\)和\(\angle CXF\)是相同的，而且因为入射光线平行于光轴，所以角度\(\angle OXC\)和\(\angle XCP\)也是一样的。因此，三角形\(CXF\)是等腰三角形，具有\(CF=FX\). 如果角度\(θ\)很小那么

\[\sin θ≈ θ \label{sma} \]

这被称为 “小角度近似值”），然后\(FX≈FP\)或\(CF≈FP\)。将其插入方程\ ref {eq31} 中作为半径\(R\)，我们得到

\[\begin{align} R &=CF+FP \nonumber \\[4pt] &=FP+FP \nonumber \\[4pt] &=2FP\nonumber \\[4pt] &=2f \end{align} \nonumber \]

换句话说，在小角度近似值中，凹面球面镜\(f\)的焦距是其曲率半径的一半，即\(R\)：

\[f=\dfrac{R}{2}. \nonumber \]

在本章中，我们假设小角度近似值（也称为近轴近似）始终有效。在这个近似值中，所有光线都是近轴射线，这意味着它们与光轴的角度很小，并且距离光轴的曲率半径要小得多。在这种情况下，它们的反射\(θ\)角度很小，所以

\[\sin θ≈ \tan θ≈ θ. \label{smallangle} \]

该图显示了凹面镜的示意图。从 O 点开始的入射光线击中 X 点的镜子。反射光线穿过 F 点。一条线 CX 将入射光线和反射光线形成的角度一分为二。这条线被标记为 R。一条平行于入射射线的直线穿过 C 点和 F 点并击中 P 点的镜子。点 F 和 P 之间的距离被标记为 f。角度 OXC、角度 CXF 和角度 XCF 都被标记为 theta。 — 图\(\PageIndex{4}\)：凹面镜中的反射。在小角度近似值中，平行于光轴 CP 的光线通过反射镜的焦点 F 反射。

使用光线追踪来定位图像

为了找到由球面镜形成的图像的位置，我们首先使用光线追踪，这是一种绘制光线并使用反射定律来确定反射光线的技术（后来，对于镜头，我们使用折射定律来确定折射光线）。结合一些基本的几何形状，我们可以使用光线追踪来查找焦点、图像位置以及有关镜子如何操纵光线的其他信息。实际上，我们已经使用了上面的光线追踪来定位球面镜的焦点或平面反射镜的成像距离。要定位对象的图像，必须找到图像的至少两个点。定位每个点需要从物体上的某个点绘制至少两条光线并构造它们的反射光线。无论是在真实空间中还是在虚拟空间中，反射光线的交叉点都是图像的相应点所在的位置。为了简化光线追踪，我们将注意力集中在四条易于构造反射的 “主” 射线上。

图中\(\PageIndex{5}\)显示了一个凹面镜和一个凸面镜，每个镜子前面都有一个箭头形的物体。这些是我们想要通过光线追踪来定位其图像的物体。为此，我们从物体上但不是光轴上的点\(Q\)绘制光线。我们选择从物体的尖端画出光线。主射线 1 从点出发\(Q\)，平行于光轴移动。如上所述，这条光线的反射必须穿过焦点。因此，对于凹面镜，主射线 1 的反射会穿过焦点\(F\)，如图所示\(\PageIndex{5b}\)。对于凸面镜，主光线 1 的反射向后延伸穿过焦点（即虚拟焦点）。主光线 2 首先在穿过焦点的线上移动，然后沿着平行于光轴的直线向后反射。主射线 3 向镜子的曲率中心移动，因此它以正常入射线击中镜子，然后沿着其来源线向后反射。最后，主射线 4 撞击镜子的顶点并围绕光轴对称反射。

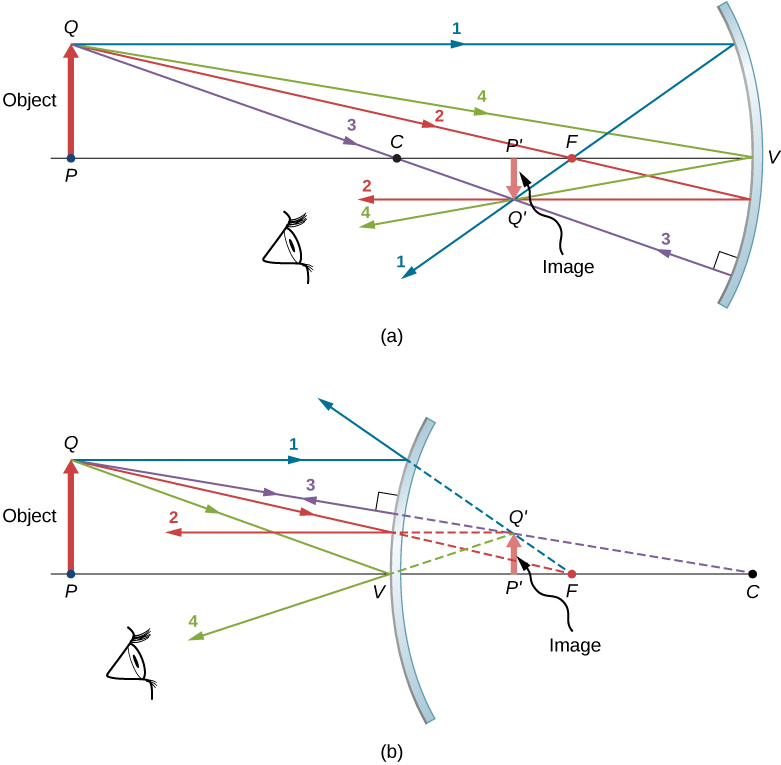
图 a 显示了凹面镜的横截面。镜子前面有一个标有底部 P 和尖端 Q 的向上箭头。一条线连接镜子上的点 P、C、F 和 V。基数 P 和尖端 Q 素数的向下箭头被标记为图像。它比物体小。 P prime 位于 C 点和 F 点之间的光轴上。四条标有 1 到 4 的入射光线源自 Q 点。所有四条反射光线在 Q 点素数处相交。图 b 显示了凸面镜的横截面。镜子前面有一个向上的箭头，标有底部 P 和尖端 Q 的物体。在连接到 C 点之前，一条从 P 点开始的直线穿过镜子上的 V 点和镜子后面的 F 点。镜子后面显示了一个较小的向上箭头、带标签的图像，其底部为 P 素数和尖端 Q 素数。 P prime 位于 V 点和 F 点之间的光轴上。四条入射光线源自 Q 点。反射光线在背面用虚线延伸，似乎都来自点 Q 素数。 — 图\(\PageIndex{5}\)：所示为（a）凹面镜和（b）凸面镜的四条主光线。图像形成于光线相交的地方（对于真实图像）或光线向后延伸的交叉处（对于虚拟图像）。

四条主光线在点处相交\(Q′\)，点\(Q\)是点的图像所在的位置。要定位点\(Q′\)，绘制任意两条主光线就足够了。因此，我们可以自由选择我们想要定位图像的主光线。绘制两条以上的主光线有时有助于验证光线追踪是否正确。

要完全定位扩展图像，我们需要在图像中找到第二个点，这样我们才能知道图像的方向如何。为此，我们追踪来自物体底部的主光线。在这种情况下，所有四条主光线都沿着光轴运行，从镜面反射，然后沿着光轴返回。困难在于，由于这些光线是共线的，因此我们无法确定它们相交的唯一点。我们所知道的只是图像的基础位于光轴上。但是，由于镜子从上到下都是对称的，因此它不会改变物体的垂直方向。因此，由于物体是垂直的，因此图像必须是垂直的。因此，如图所示，物体底部的图像位于光轴上，位于尖端图像的正上方。

对于凹面镜，在这种情况下，延伸图像在镜子的焦点和曲率中心之间形成。它相对于物体是反向的，是真实的图像，并且比物体小。如果我们将物体移到离镜子更近或更远的地方，图像的特征就会改变。例如，我们在后面的练习中表明，放置在凹面镜和焦点之间的物体会产生直立且比物体大的虚拟图像。对于凸面镜，扩展图像在焦点和镜子之间形成。它相对于物体是直立的，是虚拟图像，比物体小。

光线追踪规则

光线追踪对镜像非常有用。这里总结了光线追踪的规则，以供参考：

平行于球面镜光轴移动的光线沿着穿过镜面焦点的直线反射（图中的射线 1\(\PageIndex{5}\)）。
沿着穿过球面镜焦点的直线传播的光线沿着一条平行于镜面光轴的直线（图中的射线 2\(\PageIndex{5}\)）反射。
沿着穿过球面镜曲率中心的直线传播的射线沿着同一条线（图中的射线 3\(\PageIndex{5}\)）反射回来。
撞击球面镜顶点的射线围绕镜的光轴对称反射（图中的射线 4\(\PageIndex{5}\)）。

我们使用光线追踪来说明镜子是如何形成图像的，并获得有关镜子光学特性的数值信息。如果我们假设镜子与其曲率半径相比很小，我们也可以使用代数和几何来推导镜像方程，我们将在下一节中进行介绍。将光线追踪与镜像方程相结合是分析镜像系统的好方法。

通过反射形成图像——镜像方程

对于平面镜，我们证明形成的图像具有与物体相同的高度和方向，并且它位于镜子后面的距离与物体在镜子前面的距离相同。尽管曲面镜的情况稍微复杂一些，但使用几何结构可以得出将物体和图像距离与凹面和凸面镜的焦距联系起来的简单公式。

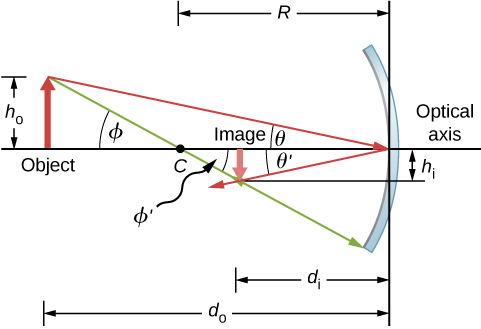
图中显示了一个凹面镜、一个物体、它的倒影和光轴。物体的高度为 h 下标 o，图像的高度为 h 下标 i。物体和图像与镜像的距离分别为 d 下标 o 和 d 下标 i。两条光线来自物体的尖端。射线 1 在光轴上击中镜子，与光轴形成一个角度 theta。反射光线与轴线形成角度 theta prime 并穿过图像的尖端。射线 2 在点 C 处与轴线相交，形成相反的角度 phi 和 phi prime。它在撞到镜子之前会穿过图像的尖端。 — 图\(\PageIndex{6}\)：由凹面镜形成的图像。

以图\(OP\)中所示的对象为例\(\PageIndex{6}\)。镜子的曲率中心已标记，\(C\)与镜子顶点有一段距\(R\)离，如图所示。物体和图像的距离标记为 “\(d_o\)和”\(d_i\)，物体和图像的高度分别标记为 “\(h_o\)和\(h_i\)”。因为角度\(ϕ\)和\(ϕ′\)是交替的内角，所以我们知道它们具有相同的大小。但是，如果我们测量与光轴的角度，它们的符号必须不同，所以\(ϕ=−ϕ′\)。类似的场景适用于角度\(θ\)和\(θ′\)。反射定律告诉我们，它们具有相同的大小，但是如果我们测量与光轴的角度，它们的符号必须不同。因此，\(θ=−θ′\)。取角度的正切\(θ\)值\(θ′\)，然后使用它给我们的属性\(\tan(−θ)=−\tan θ\)

\[\left. \begin{array}{rcl} \tanθ=\dfrac{h_o}{d_o} \\ \tanθ′=−\tanθ=\dfrac{h_i}{d_i} \end{array}\right\} =\dfrac{h_o}{d_o}=−\dfrac{h_i}{d_i} \label{eq51} \]

要么

\[- \dfrac{h_o}{h_i}=\dfrac{d_o}{d_i}.\label{eq52} \]

同样，取\(ϕ\)和的切线\(ϕ′\)给出

\[\left. \begin{array}{rcl} \tanϕ=\dfrac{h_o}{d_o-R} \\ \tanϕ′=−\tanϕ=\dfrac{h_i}{R-d_i} \end{array}\right\} =\dfrac{h_o}{d_o-R}=−\dfrac{h_i}{R-d_i} \nonumber \]

要么

\[−\dfrac{h_o}{h_i}=\dfrac{d_o-R}{R-d_i}. \label{eq55} \]

将方程\ ref {eq51} 和\ ref {eq55} 组合得出

\[\dfrac{d_o}{d_i}=\dfrac{d_o−R}{R−d_i}. \nonumber \]

经过一点代数之后，这就变成了

\[\dfrac{1}{d_o}+\dfrac{1}{d_i}=\dfrac{2}{R}. \label{eq57} \]

此结果不需要近似值，因此它是精确的。但是，如上所述，在小角度近似值中，球面镜的焦距是镜面曲率半径的一半，或\(f=R/2\)。将其插入方程式\ ref {eq57} 可以得出镜像方程：

\[\underbrace{ \dfrac{1}{d_o}+\dfrac{1}{d_i}=\dfrac{1}{f}}_{\text{mirror equation}}. \label{mirror equation} \]

镜像方程将图像和物体距离与焦距相关联，仅在小角度近似值中有效（方程\ ref {sma}）。尽管它是为凹镜而衍生的，但它也适用于凸面镜（证明这是一种练习）。我们可以将镜像方程扩展到平面镜的情况，方法是注意到平面镜的曲率半径是无限的。这意味着焦点位于无穷大，因此镜像方程简化为

\[d_o=−d_i \nonumber \]

这与之前获得的方程相同。

请注意，在推导镜像方程时，我们对符号非常谨慎。对于平面镜，图像距离与物体距离的符号相反。此外，图\(\PageIndex{6}\)中凹面镜形成的真实图像相对于物体位于光轴的另一侧。在这种情况下，图像高度应具有与物体高度相反的符号。为了跟踪镜像方程中各种量的符号，我们现在引入了符号惯例。

球面反射镜的签名惯例

在几何光学中，使用一致的符号惯例非常重要。它为表征光学系统的量分配正值或负值。了解符号惯例允许您在不构造射线图的情况下描述图像。此文本使用以下符号惯例：

凹面镜的焦距\(f\)为正，凸面镜的焦距为负。
真实图像的图像\(d_i\)距离为正，虚拟图像的图像距离为负。

请注意，规则 1 意味着球面镜的曲率半径可以是正的也可以是负的。曲率半径为负意味着什么？这仅仅意味着凸面镜的曲率半径被定义为负数。

图像放大倍率

让我们使用符号惯例来进一步解释镜像方程的推导。在得出这个方程时，我们发现物体和图像的高度相关性为

\[−\dfrac{h_o}{h_i}=\dfrac{d_o}{d_i}. \label{eq61} \]

参见方程\ ref {eq52}。物体和图中镜子形成的图像\(\PageIndex{6}\)都是真实的，因此物体和图像的距离都是正的。物体的最高点位于光轴上方，因此物体高度为正。但是，图像位于光轴以下，因此图像高度为负。因此，这种符号惯例与我们对镜像方程的推导是一致的。

实际上，方程\ ref {eq61} 用物体和图像距离描述了图像的线性放大率（通常简称为 “放大倍率”）。因此，我们将无量纲放大倍数定义\(m\)如下：

\[\underbrace{m=\dfrac{h_i}{h_o}}_{\text{linear magnification}}. \label{mag} \]

如果\(m\)是正数，则图像是直立的；如果\(m\)是负数，则图像是反向的。如果\(|m|>1\)，则图像大于物体；如果\(|m|<1\)，则图像小于对象。有了这个放大率的定义，我们得出了垂直和水平物体与图像距离之间的以下关系：

\[m=\dfrac{h_i}{h_o}=−\dfrac{d_i}{d_o}. \nonumber \]

这是一个非常有用的关系，因为它可以让你从物体和图像距离中获得图像的放大倍数，你可以从镜像方程中获得。

示例\(\PageIndex{1}\): Solar Electric Generating System

当今用于发电的太阳能技术之一涉及一种设备（称为抛物线槽或聚光收集器），该设备将阳光集中在含有流体的变黑管道上。这种加热的流体被泵送到热交换器，然后将热能转移到另一个系统，该系统用于产生蒸汽，并最终通过传统的蒸汽循环发电。 \(\PageIndex{7}\)该图显示了南加州这样的工作系统。真正的镜子是一个抛物线圆柱体，其焦点位于管道上；但是，我们可以将镜子近似为圆柱体的四分之一。

图\(\PageIndex{7}\)：在南加州，抛物线槽式集热器用于发电。（来源：“kjkolb” /维基共享资源）

如果我们想让来自太阳的光线聚焦在距离镜子 40.0 cm 的地方，镜子的半径是多少？
假设日照（入射太阳辐射）为 900 W/m ²，每米管道长度聚集在管道上的阳光量是多少？
如果输液管的直径为 2.00 厘米，则在 1 分钟内，每米管道的流体温度升高是多少？假设所有入射在反射镜上的太阳辐射都被管道吸收，并且流体是矿物油。

策略

首先确定所涉及的物理原理。第 (a) 部分与球面反射镜的光学有关。第 (b) 部分涉及一点数学，主要是几何。第 (c) 部分要求了解热量和密度。

解决方案

a. 太阳是物体，所以物体的距离本质上是无穷大：\(d_o=\infty\)。所需的图像距离为\(d_i=40.0\,cm\)。我们使用镜像方程（方程\ ref {镜像方程}）来计算镜子的焦距：

\[\begin{align*} \dfrac{1}{d_o}+\dfrac{1}{d_i} &=\dfrac{1}{f} \nonumber \\[4pt] f &= \left(\dfrac{1}{d_o}+\dfrac{1}{d_i}\right)^{−1} \\[4pt] &= \left(\dfrac{1}{\infty}+\dfrac{1}{40.0\,cm}\right)^{−1} \\[4pt] &= 40.0 \,cm \end{align*} \nonumber \]

因此，镜子的半径为

\[R=2f=80.0\,cm. \nonumber \]

b. 日照量为 900 W/m ²。你必须找到凹面镜\(A\)的横截面积，因为传递的功率是\(900\, W/m^2×A\)。在这种情况下，镜子是圆柱体的四分之一部分，因此镜子一定长\(L\)度的面积为\(A=\frac{1}{4}(2πR)L\)。那么长度为 1.00 m 的面积就是

\[\begin{align*} A&=\dfrac{\pi}{2}R(1.00m) \\[4pt] &=\dfrac{(3.14)}{2}(0.800\,m)(1.00\,m) \\[4pt] &=1.26\,m^2. \end{align*} \nonumber \]

然后，长度为 1.00 米的管道上的日照就是

\[(9.00×10^2\dfrac{W}{m^2})(1.26\,m^2)=1130\,W. \nonumber \]

c. 温度的升高由下式给出\(Q=mcΔT\)。管道一米段中矿物油的质量\(m\)为

\[ \begin{align*} m &= ρV = ρπ\left(\dfrac{d}{2}\right)^2(1.00\,m) \nonumber \\[4pt] &=(8.00×10^2kg/m^3)(3.14)(0.0100\,m)^2(1.00\,m) \nonumber \\[4pt] &=0.251\,kg \end{align*} \nonumber \]

因此，一分钟内温度升高是

\[ \begin{align*} \Delta T&= \dfrac{Q}{mc} \nonumber \\[4pt] &=\dfrac{(1130\,W)(60.0\,s)}{(0.251\,kg)(1670\,J⋅kg/°C)} \nonumber \\[4pt] &=162°\end{align*} \nonumber \]

意义

加利福尼亚沙漠中的一系列这样的管道在阳光明媚的日子里可以提供 250 兆瓦的热输出，液体的温度高达 400°C。我们考虑这里只建造一米的管道，而忽略了管道沿线的热量损失。

示例\(\PageIndex{2}\): Image in a Convex Mirror

角膜曲率计是一种用于测量眼角膜曲率的设备，特别是用于安装隐形眼镜的设备。光线从角膜反射出来，角膜就像凸面镜，角膜曲率计测量图像的放大倍率。放大倍数越小，角膜曲率半径越小。如果光源距离角膜 12 厘米，图像放大倍率为 0.032，那么角膜的曲率半径是多少？

策略

如果你找到由角膜形成的凸镜的焦距，那么你就知道它的曲率半径（它是焦距的两倍）。物体距离为 d _o =12cm，放大倍率为 m=0.032。首先找到图像距离，\(d_i\)然后求解焦距\(f\)。

解决方案

从放大率方程（方程\ ref {mag}）开始，求解\(d_i\)并插入给定值得出

\[d_i=−m d_o=−(0.032)(12\,cm)=−0.384\,cm \nonumber \]

我们保留了一个特别重要的数字，因为这是计算的中间步骤。求解焦距的镜像方程\(f\)并插入物体和图像距离的已知值。结果是

\[ \begin{align*} \dfrac{1}{d_o}+\dfrac{1}{d_i} &= \dfrac{1}{f} \\[4pt] f &= \left(\dfrac{1}{d_o}+\dfrac{1}{d_i}\right)^{−1} \\[4pt] &= \left(\dfrac{1}{12cm}+\dfrac{1}{-0.384cm}\right)^{−1} \\[4pt] &=-40.0 \,cm \end{align*} \nonumber \]

曲率半径是焦距的两倍，所以

\[R=2f=−0.80\,cm \nonumber \]

意义

焦距为负，因此焦点是虚拟的，正如凹面镜和真实物体所预期的那样。此处找到的曲率半径对于角膜来说是合理的。成人眼角膜到视网膜的距离约为 2.0 cm。实际上，角膜可能不是球形的，这使得安装隐形眼镜的工作变得复杂。请注意，此处的图像距离为负数，这与图像在镜子后面的事实一致。因此，图像是虚拟的，因为实际上没有光线穿过它。在问题和练习中，您将表明，对于固定的物体距离，较小的曲率半径对应于放大倍率越小。

问题解决策略：球面反射镜

第 1 步。首先确保涉及球面镜的图像形成。
第 2 步。确定是否需要光线追踪、镜像方程或两者兼而有之。即使问题没有特别要求光线追踪，草图也非常有用。在草图上写下符号和已知值。
第 3 步。准确确定问题中需要确定的内容（找出未知数）。
第 4 步。如上所述，列出给出或可以从问题中推断出的内容（找出已知数）。
第 5 步。如果需要光线追踪，请使用本节开头附近列出的光线追踪规则。
第 6 步。大多数定量问题都需要使用镜像方程。使用示例作为使用镜像方程的指南。
第 7 步。检查答案是否合理。物体距离、图像距离和焦距的符号是否与光线追踪的预期相对应？放大率的符号是否正确？物体和图像的距离是否合理？

偏离小角度近似值

小角度近似值（方程\ ref {smallangle}）是上述关于球面镜形成图像的讨论的基石。当违反这个近似值时，球面镜创建的图像就会失真。这种失真称为像差。在这里，我们简要讨论两种特定类型的像差：球像差和昏迷。

球面像差

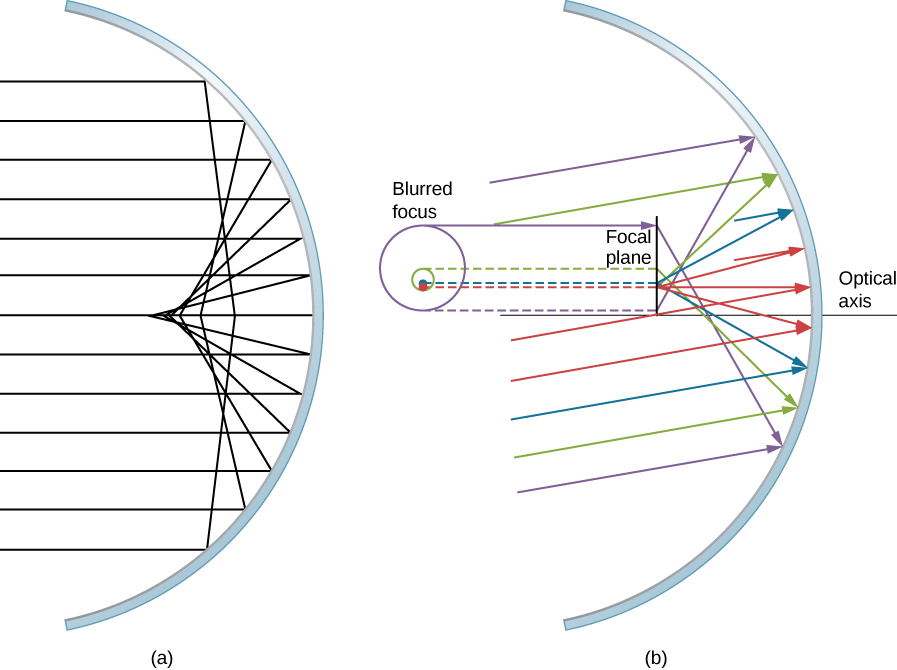
假设一束宽阔的平行光线撞击球面镜，如图所示\(\PageIndex{8}\)。光线照射到的光轴越远，球面镜与抛物线镜的近似度就越差。因此，这些光线与光轴附近的光线聚焦在同一点上，如图所示。由于球面像差，球面镜中延伸物体的图像会变得模糊。球面像差是我们在本章下一节中考虑的反射镜和透镜的特征（需要更复杂的镜子和透镜来消除球面像差）。

图 a 显示了凹面镜的横截面，其中有几条光线平行于光轴入射在其上。反射光线在光轴上的不同点汇聚。从离轴线更远的点反射的光线会聚到离镜子更近的地方。图 b 显示了有几条射线入射的凹面镜的横截面。这些光线彼此平行，但与轴成角度。一条标有焦平面的直线垂直于光轴，并且在镜子前面稍微有一段距离。反射光线在不同的位置击中这条线。焦平面的正面视图显示为圆圈，标签模糊了焦点。 — 图\(\PageIndex{8}\)：（a）使用球差时，距离光轴较远的光线和更接近光轴的光线聚焦在不同的点。请注意，对于距离光轴较远的光线，像差会变得更严重。 (b) 对于彗星像差，与光轴不平行的平行光线聚焦在不同的高度和不同的焦距，因此图像包含像彗星一样的 “尾巴”（在拉丁语中为 “昏迷”）。请注意，彩色光线仅用于便于观看；颜色并不表示光线的颜色。

昏迷或昏迷像差

昏迷与球面像差类似，但是当入射光线不平行于光轴时就会出现，如图所示\(\PageIndex{8b}\)。回想一下，小角度近似值适用于与其半径相比较小的球面反射镜。在这种情况下，球面镜是抛物线反射镜的好近似值。抛物线反射镜将所有平行于光轴的光线聚焦在焦点。但是，不平行于光轴的平行光线聚焦在不同的高度和不同的焦距，如图所示\(\PageIndex{8b}\)。由于球面镜围绕光轴对称，因此该图中的各种彩色光线在焦平面上形成了相应颜色的圆圈。

尽管球面镜如图所示\(\PageIndex{8b}\)，但抛物线反射镜也会出现昏迷像差——它不是由小角度近似值（方程\ ref {smallangle}）的分解造成的。但是，球面像差仅出现在球面反射镜上，这是小角度近似值中断的结果。我们将在本章后面讨论与望远镜相关的昏迷和球面像差。