1.7: 惠更斯原理

Last updated
Save as PDF

Page ID: 202082

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

在本节结束时，您将能够：

描述惠更斯的原理
使用惠更斯原理来解释反射定律
使用惠更斯原理来解释折射定律
使用惠更斯原理来解释衍射

到目前为止，在本章中，我们一直在使用光的射线模型讨论光学现象。但是，有些现象需要根据光的波浪特性进行分析和解释。当波长与光学器件的尺寸相比不可忽略时（例如衍射时的狭缝），尤其如此。惠更斯原理是进行这种分析的必不可少的工具。

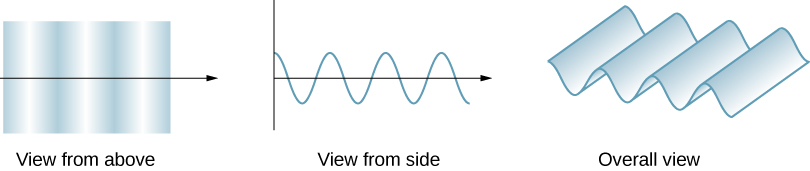
\(\PageIndex{1}\)该图显示了从上方和侧面观察横向波浪的外观。可以想象光波会像这样传播，尽管我们实际上没有看到它在太空中摆动。从上方看，我们观察波锋（或波峰），就好像我们在向下看海浪一样。侧视图将是电场或磁场的图表。上面的视图在开发有关波动光学的概念时可能更有用。

三个数字包含波浪的三个视图。第一个是从上面看的景色。波浪向右传播，并以一系列垂直条带的形式出现，这些条带逐渐从深色变为浅色，然后重复。下一个视图是侧面视图。波浪再次向右传播，显示为正弦曲线，在指向右侧的黑色箭头上方和下方振荡，该箭头用作水平轴。第三是总体视图。这是波长的透视图，波长与前两张图像中的波长相同，看起来像起伏的表面。 — 图\(\PageIndex{1}\)：从上方和侧面观察的横向波，例如电磁光波。传播方向垂直于波锋（或波峰），由射线表示。

荷兰科学家克里斯蒂安·惠更斯（1629—1695 年）开发了一种有用的技术，用于详细确定波浪传播的方式和地点。从某个已知的位置出发，惠更斯原理指出，波锋上的每个点都是小波的来源，这些小波以与波浪本身相同的速度向前扩散。新波前线与所有小波相切。

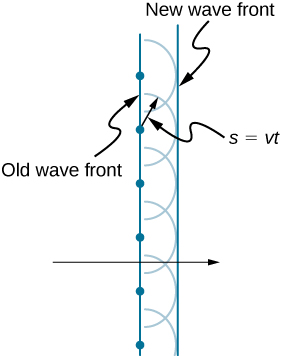
\(\PageIndex{2}\)该图显示了惠更斯原理是如何应用的。波浪前线是指随着波峰或波谷移动的长边。波前面的每个点都会发出一个以传播速度移动的半圆波浪\(v\)。我们可以\(t\)稍后再画出这些小波，这样它们就可以移动了一段距离\(s=vt\)。新的波浪阵线是一个与小波相切的平面，也是我们所期望的波浪\(t\) 稍后会出现的样子。惠更斯的原理适用于所有类型的波浪，包括水波、声波和光波。它不仅可用于描述光波如何传播，还可用于解释反射和折射定律。此外，我们将看到惠更斯的原理告诉我们光线的干扰方式和位置。

此图显示了两条垂直直线，其中左线标记为旧波浪前线，右线标记为新波浪前线。在图像的中央，一个横向的黑色箭头穿过两条线并指向右边。旧波浪前线穿过六个间隔均匀的点，黑色箭头上方有四个点，黑色箭头下方有四个点。每个点充当相应半圆的中心，所有八个半圆的大小相同。新的波浪正面与半圆的右边缘相切。其中一个中心点有一个径向箭头，指向相应半圆上的一个点。此径向箭头标记为 s 等于 v t。 — 图\(\PageIndex{2}\)：惠更斯原理适用于直波锋。波浪前面的每个点都会发出一个半圆形小波，该小波会移动一段距离 s=vt。新波前线是一条与小波相切的直线。

反思

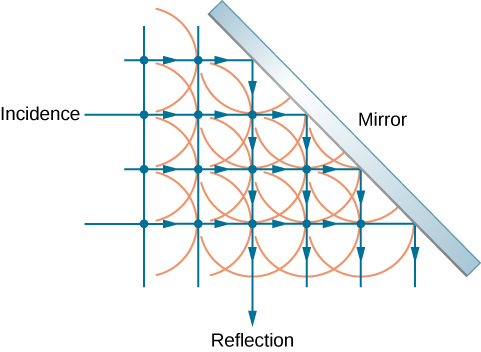
该图\(\PageIndex{3}\)显示了镜子如何以等于入射角的角度反射入射波，从而验证了反射定律。当波锋撞击镜子时，小波首先从镜子的左侧发射，然后从右侧发射。靠近左侧的小波有时间移动得更远，产生了朝所示方向移动的波锋。

该图显示了一个由四条水平、平行、相等间距的射线组成的网格，镜子向光线倾斜四十五度。光线从镜子向下反射。除了图中所示的入射光线之外，还包括另外两条来自入射光线的反射光线。点是在入射光线和反射光线的交点处绘制的。代表入射小波的朝右的半圆和用于反射小波的朝下的半圆以点为中心。 — 图\(\PageIndex{3}\)：惠更斯的原理适用于飞机波浪前线撞击镜子。所示的小波是在波浪前面的每个点撞击镜子时发射的。这些小波的切线表明，新的波锋已经以等于入射角的角度被反射。传播方向垂直于波锋，如向下箭头所示。

折射

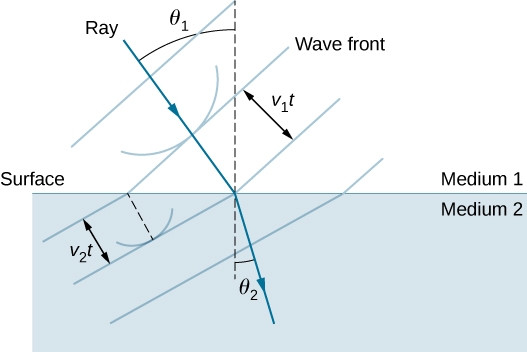
折射定律可以通过将惠更斯原理应用于从一种介质传递到另一种介质的波锋来解释（图\(\PageIndex{4}\)）。图中的每个小波都是在波前穿过介质之间的界面时发射的。由于第二种介质中的光速较小，因此波浪在给定时间内不会传播得那么远，并且新的波浪阵线会改变方向，如图所示。这就解释了为什么当光线减慢时，光线会改变方向以变得更接近垂直线。斯内尔定律可以从图\(\PageIndex{5}\) （示例\(\PageIndex{1}\)）中的几何中得出。

示例\(\PageIndex{1}\)：推导折射定律

通过检查波锋的几何形状，得出折射定律。

策略

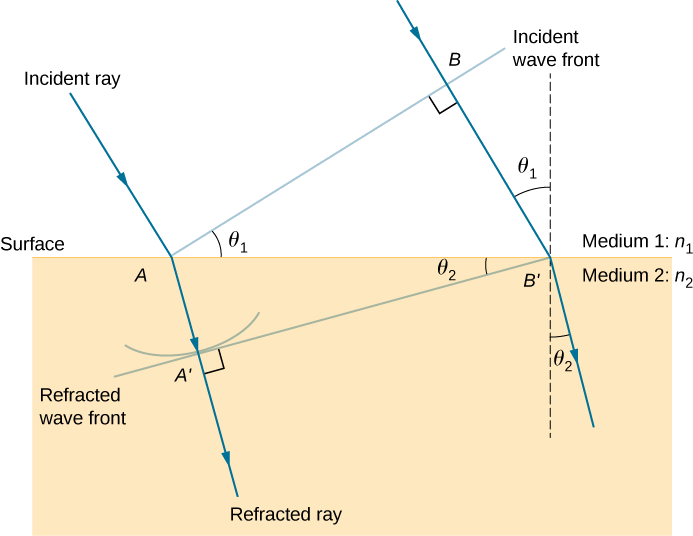
以图（图\(\PageIndex{5}\)）为例，它在图的基础上进行了扩展 \(\PageIndex{4}\)。它显示入射波阵线刚刚到达地表 A 点，而 B 点仍处于中等 1 之内。在小波从\(B\)快速到达\(B'\)表面所花费的时间\(Δt\)里\(v_1=c/n_1\)，来自的小波在哪里\(A\)移动到中等 2 的 \(AA'=v_2Δt\)距离\(v_2=c/n_2\)。请注意，在本示例中， \(v_2\)比 base\(v_1\) 慢\(n_1<n_2\)。

此图说明了光线和波锋折射的几何形状。水平表面存在于介质 1 和介质 2 之间，折射率为 n 1，折射率 n 2。图中所示为入射光线从中等 1 进入中等 2。它在点 A 处撞击表面，并在中等 2 中向法线折射。一条标有入射波前线的直线，从远离表面的点 A 开始绘制，垂直于入射线。入射波正面和表面之间的角度为 theta 1。第二条入射光线与第一条入射光线平行绘制。这条射线在标为 B 的点处与入射波前相交，并在标有 B 素数的点处撞击表面。在 B 素数处垂直于曲面绘制一条虚线。这条垂直线和第二条射线之间的角度也是 theta 1。由 A、B 和 B 素数形成的三角形是一个直角三角形，A 处的角度为 theta 1，B 处为直角。A 和 B 素数处的折射光线向下弯曲，向下垂直于表面，使垂直方向成为 theta 2 的角度。绘制了垂直于折射光线并在 B 素数处击中表面的折射波锋。这个波锋在标记为 A prime 的点处击中第一条入射射线的折射，与表面形成二的角度。 — 图\(\PageIndex{5}\)：从介质 1 到中等 2 的折射定律的几何形状。

解决方案

表面 AB' 上的分段由介质 1 内的三角形 ABB' 和介质 2 内的三角形 AA'B′ 共享。请注意，从几何图形来看，角度 BAB' 等于入射角\(θ_1\)。同样，\(∠AB'A'\)是\(θ_2\)。

AB'的长度以两种方式给出，如下所示

\ [AB'=\ dfrac {BB'} {\ sin β_1} =\ dfrac {AA'} {\ sin β_2}。 \ nonnumber\]

反转方程并用上方的 aa'=cαt/N ₂ 代替\(BB'=cΔt/n_1\)，同样，我们得到

\ [\ dfrac {\ sin β _1} {c\ Delta t/n_1} =\ dfrac {\ sin β _2} {c\ Delta t /n_2}。 \ nonnumber\]

取消\(cΔt\)允许我们将此方程简化为熟悉的形式

\ [\ underbrace {n_1\ sin th_1=n_2\ sin th_2} _ {\ text {斯内尔定律}}。 \ nonnumber\]

意义

尽管折射定律是由斯内尔通过实验确定的，但在这里推导出折射定律需要惠更斯的原理以及不同介质中光速不同的理解。

练习\(\PageIndex{1}\)

在示例中\(\PageIndex{1}\)，我们有\(n_1<n_2\)。 \(n_2\) 如果减小到这个水平，\(n_1>n_2\)而中等 2 中的光速比中等 1 中的光速快，那么 AA' 的长度会怎样？波锋 A'B '和折射光线的方向会怎样？

回答: AA′ 变长，A'B'倾斜得离表面更远，折射的光线偏离法线。

沃尔特·芬特（Walter Fendt）的这个小程序在你控制参数时使用惠更斯的小波展示了反射和折射的动画。请务必单击 “下一步” 以显示小波。你可以看到反射和折射的波锋正在形成。

衍射

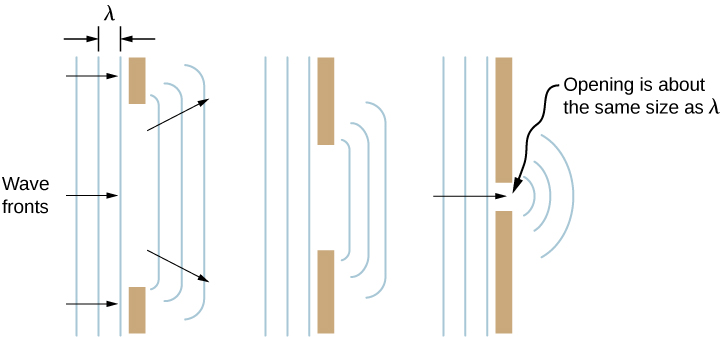
当波浪穿过开口时会发生什么，比如光线从敞开的门照进黑暗的房间？在光线方面，我们在房间的地板上观察到门口的阴影，没有可见的光线在拐角处弯曲到房间的其他部分。当声音穿过门时，我们在房间的任何地方都能听到声音，因此观察到声音在穿过这样的开口时会散开（图\(\PageIndex{6}\)）。在这种情况下，声波和光波的行为有什么区别？答案是光的波长非常短，其作用就像射线。声音的波长与门的大小差不多，在拐角处弯曲（频率为 1000 Hz，

\ [\ lambda =\ dfrac {c} {f} =\ dfrac {330\, m/s} {1000\, s^ {−1}} =0.33\, m,\ nonumber\]

大约比门口的宽度小三倍）。

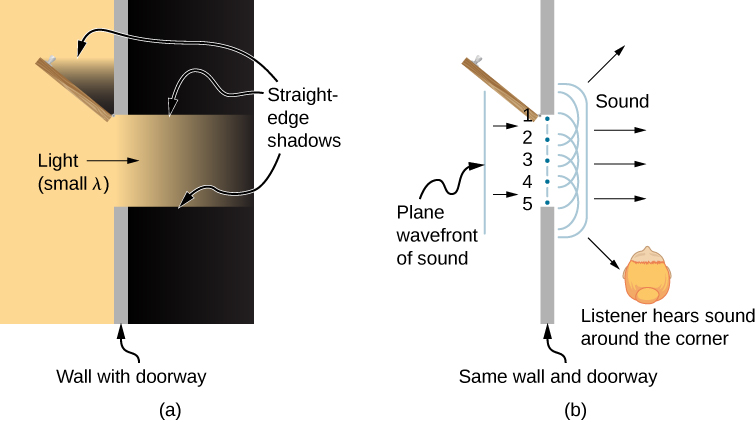
图 a 是从上方看到的一堵墙的示意图，其中有一个敞开的门口。墙从图的底部延伸到顶部，门口在墙上形成一个缝隙。门本身向左打开，距离它旋转的墙大约四十五度。标有小 lambda 的光线从墙的左侧入射。有些灯光穿过敞开的门口。穿过门的光线有锋利的边缘，对应于上方和下方的直边阴影。敞开的门还会在它和墙壁之间形成直边阴影。图中的 b 部分显示了类似的示意图。一条平行于墙壁的线从左侧接近墙壁，在声前被标记为平面波。敞开的门口上有五个均匀分布的点，标记为一到五。进入墙右侧房间的这些点的右侧出现了半圆形。将所有这些半圆括起来是一条直线，其形式是用圆角闭合方括号。这条线标有声音。显示了五条光线从包围线指向墙右边的房间。其中三条光线水平指向右边，一条光线指向上和向右，最后一条光线指向向下和向右。最后一道光线指向一个人的耳朵，我们从上面看到这个人的耳朵，他被贴上了听众的标签，在拐角处听到了声音。 — 图\(\PageIndex{6}\)：(a) 穿过门口的光线在地板上形成清晰的轮廓。由于光的波长与门的大小相比非常小，因此它的作用就像光线。 (b) 声波弯曲到房间的所有部分，这是一种波浪效应，因为它们的波长与门的大小相似。

如果我们将光线穿过狭缝等较小的开口，我们可以使用惠更斯的原理来看待光线像声音一样弯曲（图\(\PageIndex{7}\)）。波浪绕开口或障碍物边缘的弯曲称为衍射。衍射是一种波浪特征，适用于所有类型的波浪。如果观察到某种现象的衍射，则证明该现象是波浪。因此，激光束穿过图\(\PageIndex{7}\)中狭缝后的水平衍射证明了光是一种波浪。

该图显示了三张图表，说明了波浪在穿过各种大小的开口时向外扩散。每幅插图均为俯视图，入射平面波浪正面由垂直线表示。波长 lambda 是相邻线之间的距离，在所有三张图中均相同。第一张图显示波锋穿过一个开口，与波长相比该开口较宽。在开口另一侧出现的波浪锋在边缘有轻微的弯曲。第二张图显示波锋穿过一个较小的开口。波浪的弯曲程度更高，但仍有直线部分。第三张图显示波锋穿过与波长大小差不多的开口。这些波浪显示出明显的弯曲，实际上，它们看起来是圆形的，而不是直的。 — 图\(\PageIndex{7}\)：惠更斯的原理适用于飞机波浪冲击开口。波浪前部的边缘在穿过开口后会弯曲，这种过程称为衍射。对于小开口来说，弯曲量更为极端，这与波长大小差不多的物体相互作用时波浪特性最为明显的事实一致。