1.8: 两极分化

Last updated
Save as PDF

Page ID: 202066

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

在本节结束时，您将能够：

解释偏振光通过偏振滤镜时强度的变化
通过反射和布鲁斯特角计算偏振的影响
描述散射偏振的影响
解释在液晶显示器等设备中使用偏振材料的情况

我们大多数人都熟悉偏光太阳镜。它们具有减少水或玻璃反射光的特殊能力（图\(\PageIndex{1}\)）。它们之所以具有这种能力，是因为光的波浪特性称为偏振。什么是两极分化？它是如何生产的？它有哪些用途？这些问题的答案与光的波浪特性有关。

该图有两张河流同一部分的照片。在图 a 中，云层和天空反射在水中，很难看见河底的石头。在图 b 中，没有天空的反射，可以更清楚地看到河底。 — 图\(\PageIndex{1}\)：这两张河流照片显示了偏振滤镜在减少水面反射光中的眩光方面的作用。该图的 (b) 部分是用偏振滤光片拍摄的，第 (a) 部分不是。因此，在 (a) 部分中观测到的云层和天空的反射在 (b) 部分中没有观测到。偏光太阳镜在雪地和水上特别有用。（来源 a 和 credit b：“Amithshs” /Wikimedia Commons 对作品的修改）

马卢斯定律

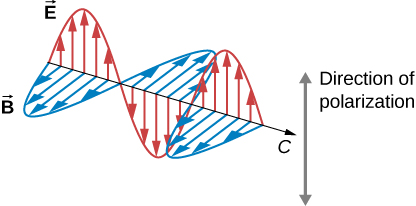
光是一种电磁（EM）波。电磁波是由垂直于传播方向振荡的不同电场和磁场组成的横向波（图 \(\PageIndex{2}\)）。但是，总的来说，电场和磁场的振荡没有特定的方向；它们在垂直于传播方向的任何随机定向平面上振动。极化是指波浪的振荡相对于波浪的传播方向确实有明确的方向。（这与讨论的电荷分离的极化类型不同。）据说具有这种方向的波浪是偏振的。对于电磁波，我们将极化方向定义为平行于电场的方向。因此，我们可以将电场箭头视为显示极化方向，如图所示 \(\PageIndex{2}\)。

以速度 c 移动的电磁波的一部分在某一时刻显示。图中显示了两个矢量分量，即 E 和 B，它们彼此垂直并垂直于传播方向。代表 E 的大小和方向的向量，显示为箭头，其尾部位于波浪的传播线上，在一个平面上形成正弦波。同样，B 向量在垂直于 E 波的平面中形成正弦波。 E 波和 B 波是同相的。极化方向由 E 向量的方向给出。 — 图\(\PageIndex{2}\)：电磁波，例如光，是横向波。电场\(\overrightarrow{E}\)和 \(\overrightarrow{B}\)磁场垂直于传播方向。波的极化方向是电场的方向。

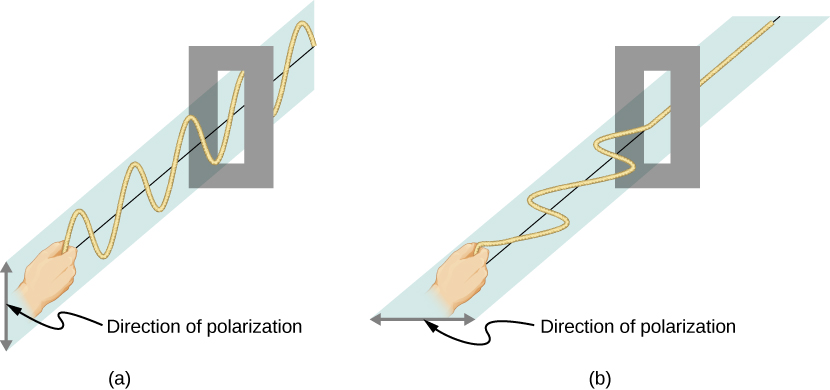
要进一步研究这个问题，请考虑图中所示绳索中的横向波浪\(\PageIndex{3}\)。一根绳子中的振荡在垂直平面上，据说是垂直极化的。另一根绳子中的那些在水平面上，是水平偏振的。如果在第一根绳子上放置一条垂直缝隙，波浪就会穿过。但是，垂直狭缝会阻挡水平偏振波。对于电磁波，电场的方向类似于绳索上的干扰。

图 a 显示了垂直摆动的绳索上穿过垂直缝隙的波浪。垂直振荡是极化的方向。图 b 显示了水平摆动的绳索上没有穿过类似垂直缝隙的波浪。水平振荡是极化的方向。 — 图\(\PageIndex{3}\)：一根绳子（a）中的横向振荡在垂直平面上，而另一根绳子（b）中的横向振荡在水平面上。据说第一个是垂直极化的，另一个据说是水平偏振的。垂直狭缝穿过垂直偏振波并阻挡水平偏振波。

太阳和许多其他光源产生的波浪具有随机方向的电场（图\(\PageIndex{1a}\)）。据说这种光是非偏振的，因为它由许多波组成，具有所有可能的偏振方向。宝丽来材料是由宝丽来公司的创始人埃德温·兰德（Edwin Land）发明的，它充当光的偏振狭缝，只允许一个方向的偏振通过。偏振滤光片由沿一个方向排列的长分子组成。如果我们将分子视为许多狭缝，类似于振荡绳索的狭缝，我们就能理解为什么只有具有特定偏振的光才能通过。偏振滤波器的轴线是滤波器通过电磁波电场的方向。

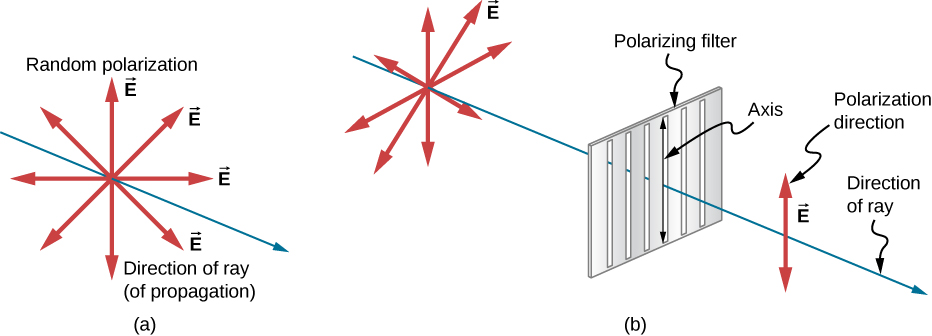
图 a 显示了一个细长的蓝色箭头，指向页面外和右侧，标有光线方向。八支红色箭头从射线上的一个点发出，标记为向量 E。这些箭头都位于垂直于射线的平面上，并且均匀地分布在射线周围。它们被标记为代表随机极化。在图 b 中，显示了一条相似但更长的光线，其红色箭头从射线左端附近的某个点发出。同一条射线上更右边的是一个细矩形，上面有六个间距相等的垂直缝隙。这个矩形被标记为偏振滤光片。其表面上的垂直双头箭头被标记为轴。滤镜右侧以光线为中心，是一个垂直方向的蓝色单向双向箭头，标有 E 和偏振方向。 — 图\(\PageIndex{4}\)：细长的箭头代表一束非偏振光。粗体箭头表示构成射线的各个波浪的极化方向。 (a) 如果光线未偏振，则箭头指向所有方向。 (b) 偏振滤波器具有偏振轴，该偏振轴充当穿过平行于其方向的电场的狭缝。电磁波的极化方向被定义为其电场的方向。

图中\(\PageIndex{5}\)显示了两个偏振滤光片对原本未偏振光的影响。第一个滤镜使光线沿其轴线偏振。当第一和第二滤光片的轴对齐（平行）时，通过第一个滤光器的所有偏振光也将通过第二个滤光器。如果旋转第二个偏振滤光片，则只有平行于第二个滤镜轴线的光分量会通过。当轴垂直时，第二个滤镜不会通过任何光线。

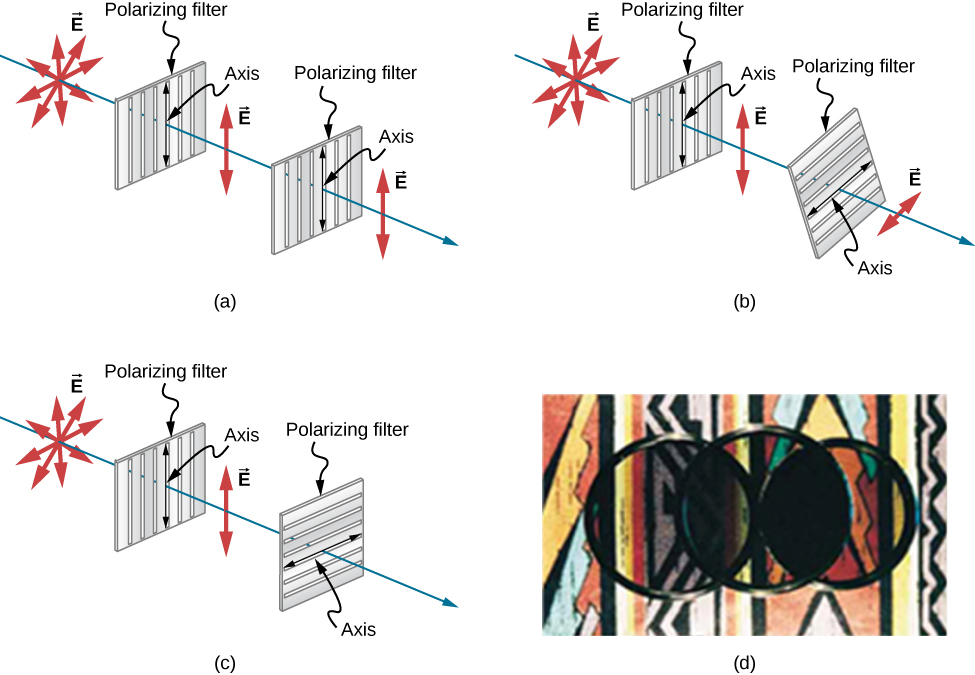
该图显示了三幅随机偏振光在不同方向上依次穿过两个偏振滤光片的插图。在图 a 中，两个滤镜的轴线彼此平行定向，在 b 中，第二个滤镜的轴与第一个滤镜的轴呈中间角度，介于 0 到 90 度之间；在 c 中，第二个滤镜的轴垂直于第一个滤波器的轴线。图 d 是实际结果的照片第一（平行）和最后（垂直）排列。在所有排列中，源光都是随机偏振的，由向量 E 箭头指向垂直于光线传播方向的平面上的每个方向表示。在所有排列中，穿过第一个滤镜（其轴线垂直定向）的光是垂直偏振的，由仅垂直向上和向下指向的 E 向量箭头表示。在图 a 中，所有偏振光都经过第二个偏振滤光片，其轴线平行于第一个偏振滤光片，并且仍处于垂直偏振状态。在图 b 中，只有一部分光通过第二个偏振滤光片，其轴线相对于第一个偏振滤光片倾斜。通过第二个滤镜的光在第二个滤镜的轴线方向上偏振，并减小 E 的大小。在图 c 中，滤镜轴彼此垂直，没有一个光线通过第二个滤镜。图 c 显示了放置在明亮彩色图案上的三个圆形光学滤镜的照片。其中两个滤镜彼此相邻放置，第三个滤镜放置在另外两个滤镜之上，因此第三个滤镜的中心位于下方两个滤镜的边缘接触的位置。有些光线穿过上部滤镜与左下方滤镜重叠的地方。没有光线穿过上部滤镜与右下滤镜重叠的地方。 — 图\(\PageIndex{5}\)：旋转两个偏振滤镜的效果，其中第一个偏振滤镜对光线进行偏振。 (a) 所有偏振光都由第二个偏振滤光片通过，因为它的轴线平行于第一个偏振滤光片。 (b) 当第二个滤镜旋转时，只有一部分光线通过。 (c) 当第二个滤光片垂直于第一个滤光片时，没有光线通过。 (d) 在这张照片中，偏光滤光片位于另外两个上方。它的轴线垂直于右边的滤镜（暗区），平行于左边的滤镜（较亮的区域）。（来源 d：P.P. Urone 对作品的修改）

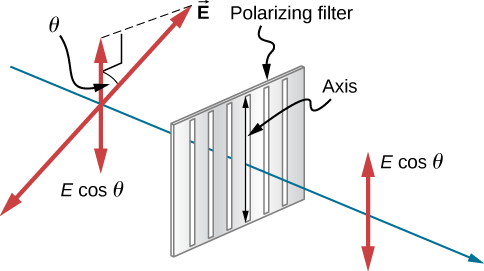
只有平行于滤波器轴线的电磁波分量才会通过。让我们称之为偏振方向和滤波器轴线之间的角度 β。如果电场的振幅为 E，则波浪的传输部分具有振幅\(E\cos θ \)（图\(\PageIndex{6}\)）。由于波浪的强度与其振幅平方成正比，因此传输波的强度 I 与入射波的强度 I 的关系为

\ [I=I_0\ cos^2β\ label {Malus's La w}\ nonumber\]

哪里\(I_0\)是偏振波在通过滤波器之前的强度。这个方程被称为马卢斯定律。

此图提供了前两幅图示意图的更多细节。在此图中，垂直定向偏振滤光片的左侧仅显示了随机偏振光源光的 E 向量中的一个，以及该向量平行于滤镜的分量。向量 E 与垂直方向成一个 theta 的角度。 E 向量的垂直分量为 E 余弦西塔。通过滤镜后，光线只有垂直的 E，大小为 E 余弦 theta。 — 图\(\PageIndex{6}\)：偏振滤光片仅传输平行于其轴线的波形分量，从而降低任何未平行于其轴线偏振的光的强度。

此开源物理动画可帮助您在光线遇到偏振滤波器时直观显示电场矢量。您可以旋转滤镜，请注意，显示的角度以弧度为单位。您也可以旋转动画以实现 3D 可视化。

示例 \(\PageIndex{1}\)：使用偏振滤波器计算强度降低

偏振光的方向和偏振滤光片的轴线之间需要多大的角度才能将其强度降低 90.0％？

策略

当强度降低 90.0% 时，它是其原始值的 10.0% 或 0.100 倍。也就是说， 我=0.100I ₀。利用这些信息，方程 I=I ₀ cos ² β 可用于求解所需的角度。

解决方案

求解马卢斯定律（方程\ ref {Malus's Law}），\(\cos θ\) 然后用 I 和 I 之间的关系代替 ₀ 得出

\[\cos θ=\dfrac{I}{I_0}=\frac{0.100I_0}{I_0}=0.3162. \nonumber \]

求解\(θ\)收益率

\[θ=\cos^{−1}0.3162=71.6°. \nonumber \]

意义

要将强度降低到其原始值的10.0％，需要在偏振方向和滤波器轴之间有一个相当大的角度。从偏光薄膜的实验来看，这似乎是合理的。有趣的是，在 45° 的角度下，强度会降低到其原始值的 50%。请注意，71.6° 等于将强度降低到零的 18.4°，在 18.4° 的角度下，强度会降低到其原始值的 90.0%，这就证明了对称性。

练习\(\PageIndex{1}\)

尽管我们在示例中没有指定方向\(\PageIndex{1}\)，但假设偏振滤镜顺时针旋转了 71.6°，从而将光强降低了 90.0%。如果偏振滤光片逆时针旋转 71.6°，强度会降低多少？

回答: 也是 90.0%

反射偏振

到目前为止，你可能会猜到偏光太阳镜可以减少反射光中的眩光，因为反射光是偏光的。你可以亲自检查一下，把偏光太阳镜放在你面前，一边旋转太阳镜，一边看着水或玻璃反射的光。当你旋转太阳镜时，你会注意到光线变得明亮而昏暗，但不是完全变黑。这意味着反射光是部分偏振的，不能被偏振滤镜完全阻挡。

该图\(\PageIndex{7}\)说明了当非偏振光从表面反射时会发生什么。垂直偏振光优先在表面折射，因此反射光的水平偏振程度更高。这种现象的原因超出了本文的范围，但记住这一点的一个方便的助记符是将两极分化方向想象成一支箭。垂直偏振就像垂直于表面的箭头，更容易粘住而不被反射。水平偏振就像箭头在其侧面弹跳，更有可能被反射。因此，与来自其他来源的非偏振光相比，带有垂直轴的太阳镜可以阻挡更多的反射光。

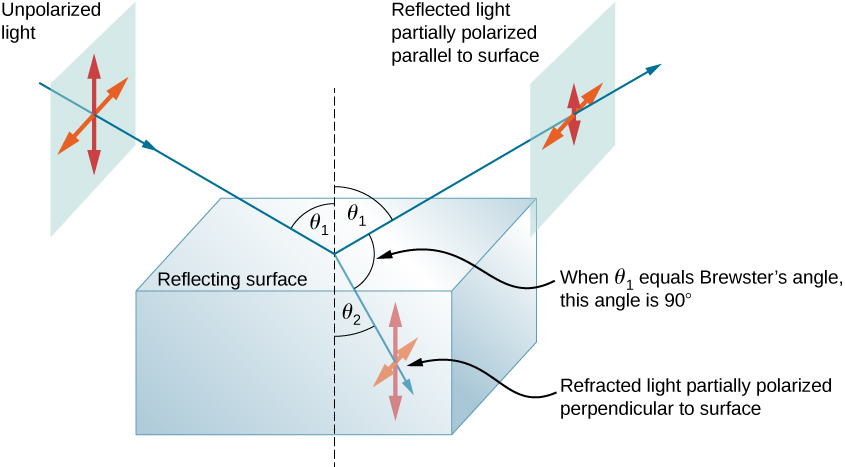
该图显示了空气中的一块玻璃块。反射面是水平的。标有非偏振光的光线从左上角开始，击中方块的中心，与垂直方向成一角度 theta 1。以这条入射线为中心的是两个双头箭头，一个是水平的，另一个是垂直的。从这条射线击中玻璃块的那一刻起，就会出现两条射线。一个是反射光线，它以 theta 的角度向上和向右移动，一个是向上和向右移动的折射射线，它与垂直方向成了 theta 2 的角度向下和向右移动。反射光被标记为平行于表面的部分偏振。两个双头箭头，与入射射线上的箭头类似，以反射光线为中心显示，但垂直箭头比水平箭头短得多。折射的光线被标记为垂直于表面的部分偏振。两个双头箭头，与入射射线上的箭头类似，以反射光线为中心显示，但水平箭头比垂直箭头短得多。注释表明，当 theta one 等于 Brewster 的角度时，反射光线和折射光线之间的角度为九十度。 — 图\(\PageIndex{7}\)：反射产生的偏振。非偏振光的垂直和水平偏振量相等。与表面相互作用后，垂直分量优先被吸收或折射，从而使反射光更加水平偏振。这类似于箭击中它们的侧面然后弹起来，而击中尖端的箭会进入水面。

由于未反射的光部分是折射的，因此偏振量取决于所涉及介质的折射指数。可以看出，反射光是以反射角完全偏振的 β _b 由下式给出

\[tan \, θ_b=\frac{n_2}{n_1} \nonumber \]

其中 n ₁ 是入射和反射光传播的介质，n ₂ 是构成反射光的界面的介质的折射率。这个方程被称为布鲁斯特定律，β _b 被称为布鲁斯特角，以发现它们的十九世纪苏格兰物理学家的名字命名。

这个开源物理动画将入射光、反射光和折射光显示为射线和电磁波。尝试旋转动画以实现 3D 可视化，同时更改入射角度。在布鲁斯特的角度附近，反射的光会变得高度偏振。

示例 \(\PageIndex{2}\)：通过反射计算偏振

(a) 当从水中反射时，在空气中传播的光会以什么角度完全水平偏振？ (b) 来自玻璃？

策略

解决这些问题所需要的只是折射指数。空气有 n ₁ =1.00，水有 n ₂ =1.333，皇冠玻璃有 n′ ₂ =1.520。在每种情况下，均\(tan \, θ_b=\frac{n_2}{n_1}\)可直接应用该方程来找出 β _b。

解决方案

a. 将已知量放入方程中

\[\tan \, θ_b=\frac{n_2}{n_1} \nonumber \]

给

\[\tan \, θ_b=\frac{n_2}{n_1}=\frac{1.333}{1.00}=1.333. \nonumber \]

求解角度 β _会得到

\[θ_b=tan^{−1}1.333=53.1°. \nonumber \]

b. 同样，对于皇冠玻璃和空气，

\[tan \, θ′_b=\frac{n′_2}{n_1}=\frac{1.520}{1.00}=1.52. \nonumber \]

因此，

\[θ′_b=tan^{−1}1.52=56.7°. \nonumber \]

意义

在这些角度反射的光线可以被保持轴线垂直的良好偏振滤光片完全阻挡。布鲁斯特对水和空气的角度与玻璃和空气的角度相似，因此在类似情况下，太阳镜对水或玻璃反射的光同样有效。未反射的光会被折射到这些介质中。因此，在等于布鲁斯特角度的入射角下，折射的光在垂直方向上会稍微偏振。它不是完全垂直偏振的，因为只有一小部分入射光被反射，因此大量的水平偏振光会被折射。

练习\(\PageIndex{2}\)

如果原始入射光已经 100% 垂直偏振，那么在布鲁斯特的角度会发生什么？

回答: 只有折射但没有反射。

偏振滤光片的原子解释

偏振滤光片具有充当狭缝的偏振轴。该狭缝通过电场平行于轴线的电磁波（通常是可见光）。这是通过垂直于轴线对齐的长分子来实现的，如图所示 \(\PageIndex{8}\)。

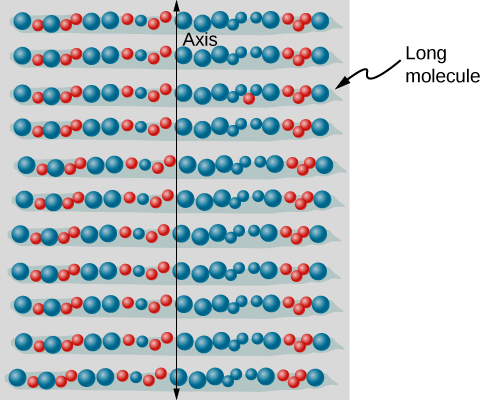
该图显示了一堆长而相同的水平分子的插图。在分子上方画一条垂直轴。 — 图\(\PageIndex{8}\)：长分子垂直于偏振滤光片的轴线对齐。在电磁波中，垂直于这些分子的电场分量通过滤波器，而与分子平行的分量被吸收。

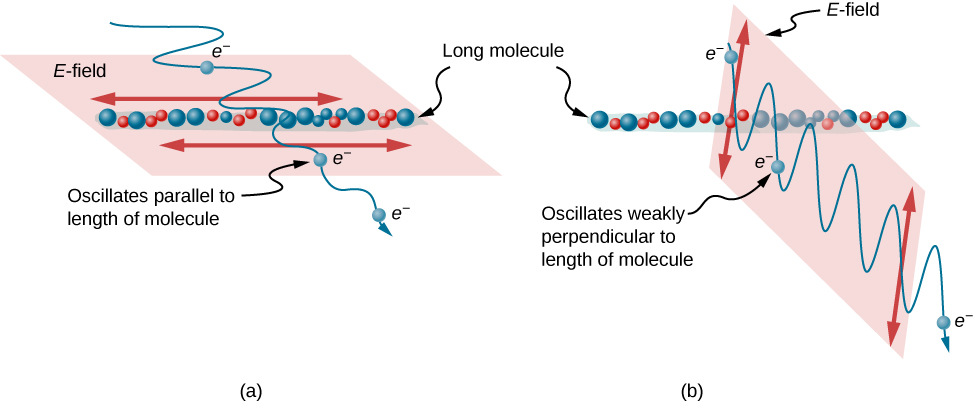
该图\(\PageIndex{9}\)说明了平行于长分子的电场分量是如何被吸收的。电磁波由振荡的电场和磁场组成。与磁场相比，电场更强，在对分子中的电荷施加力方面更有效。受影响最大的带电粒子是电子，因为电子质量很小。如果电子被迫振荡，它可以吸收来自电磁波的能量。这会减少波浪中的场，从而降低其强度。在长分子中，电子比在垂直方向上振荡更容易与分子平行振荡。电子与分子结合，在垂直于分子的运动方面受到的限制更大。因此，电子可以吸收电场分量与分子平行的电磁波。电子对垂直于分子的电场的反应要低得多，允许这些电场通过。因此，偏振滤光片的轴线垂直于分子的长度。

图 a 显示了一个长分子的图。电磁波穿过分子。波传播方向垂直于分子轴，波浪的振荡平行于分子轴。电子与分子的长度平行振荡。经过长分子后，波浪振荡的振幅显著降低。图 b 显示了相似的图，唯一的不同是波浪垂直于长分子的轴线振荡。电子微弱地垂直于分子的长度振荡。通过长分子后，电磁波的振荡幅度保持不变。 — 图\(\PageIndex{9}\)：长分子中电子与分子平行振荡的示意图。电子的振荡吸收能量并降低与分子平行的电磁波成分的强度。

散射偏振

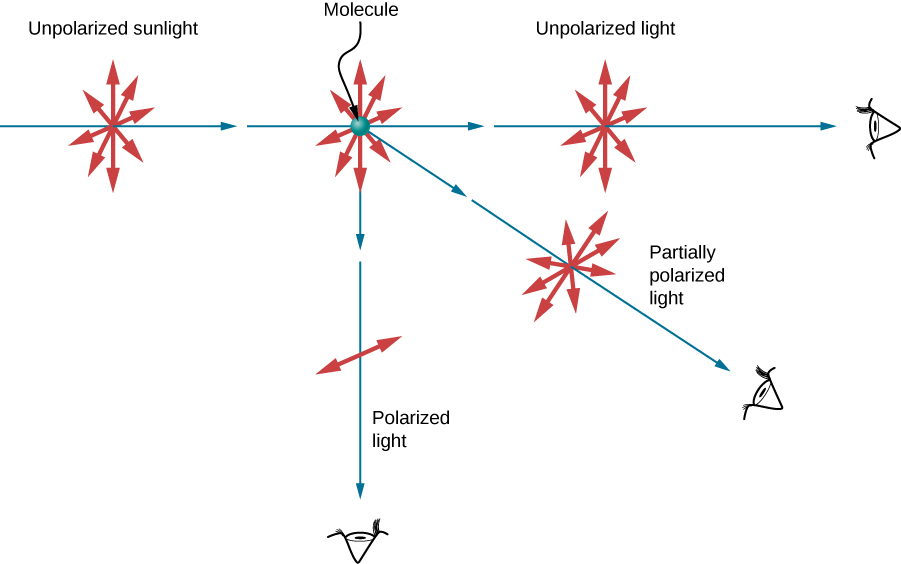
如果你把偏光太阳镜放在你面前，一边旋转它们，一边看着蓝天，你会看到天空变得明亮和昏暗。这清楚地表明空气散射的光是部分偏振的。图\(\PageIndex{10}\)有助于说明这是如何发生的。由于光是一种横向的电磁波，它使空气分子的电子垂直于其传播方向振动。然后，电子像小触角一样辐射。由于它们垂直于光线的方向振荡，因此它们会产生垂直于光线方向偏振的电磁辐射。当沿着与原始光线垂直的直线观察光线时，如图所示，散射光中不可能有平行于原始光线的偏振，因为这需要原始光线是纵波。沿着其他方向，另一个偏振的一个分量可以沿视线投射，而散射光只能部分偏振。此外，多重散射可以将来自其他方向的光线带到您的眼睛，并且可能包含不同的偏振。

该图说明了分子对非偏振光的散射。像往常一样，光线由蓝色直箭头表示，电场方向用双头红色箭头表示。非偏振入射光的电场矢量在垂直于光线的传播方向的平面上向各个方向振荡。分子将光线向各个方向散射。散射方向与入射光相同方向的光保持非偏振状态。当入射光偏振垂直于入射光线和散射光线定义的平面时，光在垂直于该方向的方向上散射。在中间方向散射的光会部分偏振。垂直于平面的电场的振幅大于平行于入射射线的电场。 — 图\(\PageIndex{10}\)：散射产生的偏振。来自空气分子的非偏振光散射会使它们的电子垂直于原始射线的方向摇动。因此，散射光的偏振垂直于原始方向，没有平行于原始方向的偏振。

偏振滤镜可以使天空的照片变暗，这是许多摄影师用来使云层更亮的技巧。来自其他颗粒（例如烟雾或灰尘）的散射也会使光偏振。检测散射电磁波中的偏振可能是确定散射源的有用分析工具。

太阳镜使用了一系列光学效果。除了偏光外，太阳镜中可能还嵌入了彩色颜料，而其他太阳镜则使用非反射涂层或反射涂层。最近的一项发展是光致变色镜片，它在阳光下变暗，在室内变得清晰。光致变色镜片嵌入了有机微晶分子，这些分子在阳光下暴露于紫外线时会改变其特性，但在没有紫外线的人工照明下会变得透明。

材料中的液晶和其他极化效应

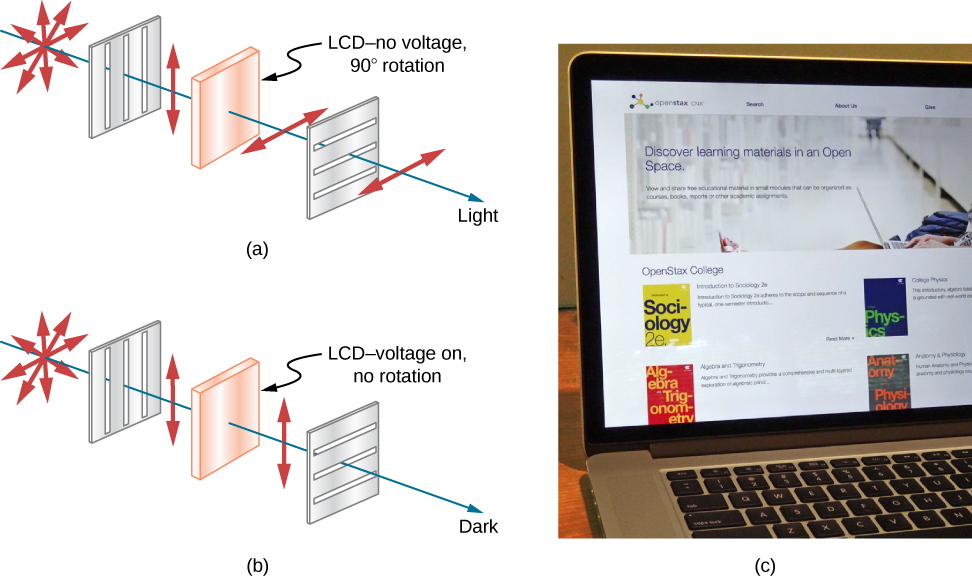
尽管毫无疑问，你知道在手表、计算器、电脑屏幕、手机、平板电视以及许多其他地方都有液晶显示器（LCD），但你可能没有意识到它们是基于偏振的。液晶之所以这样命名，是因为它们的分子即使在液体中也可以对齐。液晶的特性是它们可以将穿过它们的光的偏振旋转 90°。此外，该特性可以通过施加电压来关闭，如图所示\(\PageIndex{11}\)。可以在较小、定义明确的区域中快速操纵这一特性，从而创建我们在许多 LCD 设备中看到的对比度模式。

在平板液晶电视中，电视机背面会产生大光。光线通过数百万个称为像素（图片元素）的微小单位传播到前屏幕。其中之一如图所示\(\PageIndex{11}\)。每个单元有三个电池，带有红色、蓝色或绿色滤光片，每个单元均独立控制。当液晶两端的电压关闭时，液晶会使光线通过特定的滤波器。我们可以通过改变施加在液晶上的电压的强度来改变画面对比度。

图 a 显示了一束最初未偏振的光线穿过垂直偏振器，然后是标有 L C D 的元件，无电压旋转九十度，最后是水平偏振器。最初未偏振的光在垂直偏振器之后变为垂直偏振，然后被 L C D 元件旋转九十度，使其水平偏振，然后穿过水平偏振器。图 b 相同，只是 L C D 元件标有电压开启，不旋转。因此，从 L C D 元件发出的光是垂直偏振的，不会穿过水平偏振器，从而使该位置的区域变暗。最后，在图 c 中，显示了一张打开的笔记本电脑的照片，这样你就可以看到它的屏幕，屏幕处于开启状态，有一些图标和窗口可见。 — 图\(\PageIndex{11}\)：(a) 偏振光由液晶旋转 90°，然后由偏振滤光片通过，偏振滤光片的轴线垂直于原始偏振方向。 (b) 当向液晶施加电压时，偏振光不会旋转，而是被滤波器阻挡，使该区域与周围环境相比变暗。 (c) 液晶显示器可以制成特定颜色、体积小且速度足够快，可以在笔记本电脑和电视机中使用。

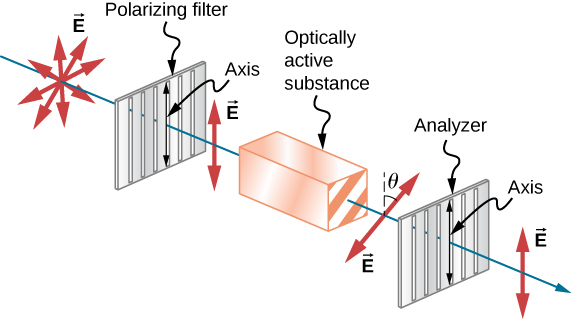
许多晶体和溶液会旋转穿过它们的光的偏振平面。据说这些物质具有光学活性。例子包括糖水、胰岛素和胶原蛋白（图\(\PageIndex{11}\)）。除了取决于物质的类型外，旋转量和方向还取决于其他几个因素。其中包括物质的浓度、光线穿过它的距离以及光的波长。光学活性是由于物质中分子的不对称形状，例如螺旋形。因此，测量偏振光穿过物质的旋转情况可用于测量浓度，这是糖的标准技术。它还可以提供有关分子形状的信息，例如蛋白质，以及影响其形状的因素，例如温度和pH值。

该图显示了最初未偏振的光线，它穿过三个光学元件。第一种是垂直偏振滤波器，因此光线穿过后电场是垂直的。接下来是标记为光学活性物质的块体。电场来自方块，相对于垂直方向旋转一个角度 theta。最后，光线穿过另一个标有分析仪的垂直偏振器。最后的电场再次垂直极化。 — 图\(\PageIndex{11}\)。光学活性是某些物质旋转穿过它们的光偏振平面的能力。使用偏振滤光片或分析仪检测旋转。

玻璃和塑料在受到压力时会产生光学活性：应力越大，效果越大。对复杂形状进行光学应力分析，方法是制作复杂形状的塑料模型，然后通过交叉滤光片进行观察，如图所示 \(\PageIndex{12}\)。显然，效果取决于波长和应力。波长依赖性有时也用于艺术目的。

该图显示了一张被夹子挤压的塑料镜头的照片。出现彩虹图案，显示镜头的变形。彩色区域由连接镜头边缘中心的深色曲线勾勒出轮廓。 — 图\(\PageIndex{13}\)：放置在交叉偏振镜之间的塑料透镜的光学应力分析。（来源： “Infopro” /Wikimedia Commons）

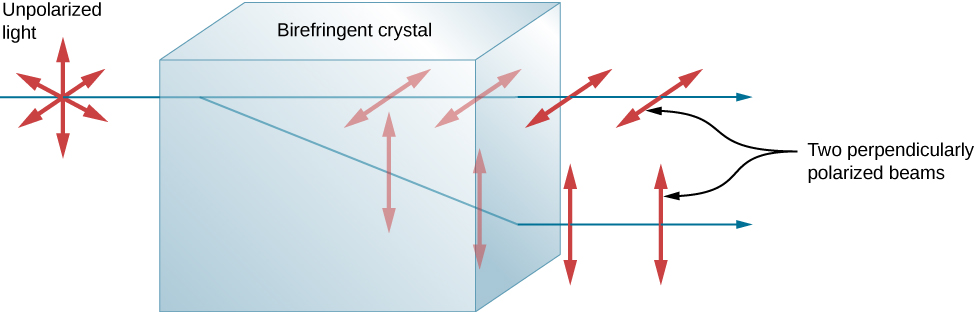
与偏振光相关的另一个有趣现象是某些晶体能够将非偏振光束分成两束偏振光束。之所以出现这种情况，是因为晶体具有一个偏振光折射率值，但垂直方向偏振光的折射率值不同，因此每个分量都有自己的折射角度。据说这种晶体是双折射的，如果正确对齐，两个垂直偏振光束将从晶体中冒出（图\(\PageIndex{14}\)）。双折射晶体可用于从非偏振光中产生偏振光束。一些双折射材料优先吸收其中一种偏振。这些材料被称为二向色性，可以通过这种优先吸收产生极化。从根本上讲，这就是偏振滤光片和其他偏振器的工作原理。

该图显示了水平的、非偏振的光线入射到标有双折射晶体的方块上。射线垂直于其进入晶体的表面。入射射线进入晶体时会分裂成两条射线。射线的一部分继续直射。这条光线是水平偏振的。射线的另一部分在 a 处传播。这条光线是垂直偏振的。第二条射线在离开晶体时会折射，使得两条射线在晶体外部平行。这些光线被标记为两个垂直偏振光束。 — 图\(\PageIndex{14}\)：双折射材料，例如普通矿物方解石，使用两个不同的折射率值将非偏振光束分成两个。