Skip to main content
Global

1.6: 分散

  1. Last updated
  2. Save as PDF
  • Page ID
    202029

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    学习目标

    在本节结束时，您将能够：

    • 解释棱镜中出现色散的原因
    • 描述分散对产生彩虹的影响
    • 总结分散的优缺点

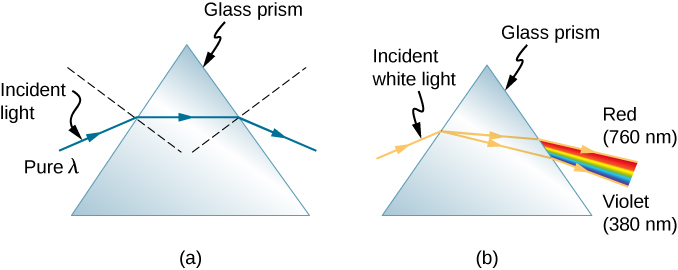
    每个人都喜欢彩虹在 黑暗的暴风雨天空中闪烁的景象。 落在清澈的雨滴上的阳光怎么 会分解成我们所看到的彩虹色？ 同样的过程 会导致白光被透明的玻璃棱镜 或钻石分解成颜色（图\(\PageIndex{1}\)）。

    图 a 是彩虹的照片。 图 b 是光线通过棱镜折射的照片。 在这两幅图中，我们可以看到平行色带：红色、橙色、黄色、绿色、蓝色和紫罗兰色。
    图\(\PageIndex{1}\)：彩虹（a） 和棱镜（b）产生的颜色相同。 （来源 a： 修改 “Alfredo55” /Wikimedia Commons 的作品；来源 b：美国宇航局对作品的 修改）

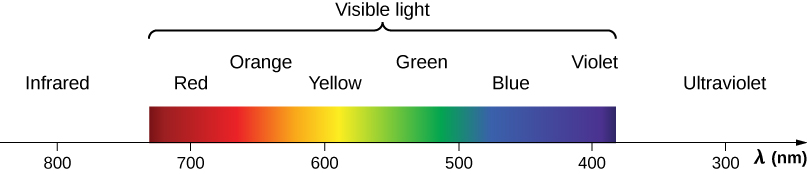
    我们在彩虹中看到大约六种颜色——红色、橙色、黄色、绿色、 蓝色和紫罗兰色；有时也会列出靛蓝。 这些颜色与不同波长的光 有关，如图所示 \(\PageIndex{2}\)。 当我们的眼睛收到纯波长的光时，我们 往往只能看到六种颜色中的一种，具体取决于波长。 在其他情况下，我们可以感知到的数千种其他色调是 我们的眼睛对各种波长混合的反应。 特别是白光是所有可见 波长的相当均匀的混合物。 阳光被认为是白色，实际上看起来有点黄，因为它的波长 是混合的，但它确实 包含所有可见波长。 彩虹中的颜色顺序 与图中显示的颜色顺序相同。 这意味着白光根据 波长分散在彩虹中。 色散被定义为将白光扩散 到其整个波长光谱中。 从技术上讲，每当光的传播取决于波长时，就会 发生色散。

    该图显示了与不同波长光相关的颜色，按波长 lambda 递减顺序排列，以纳米为单位测量。 红外线从 800 纳米开始。 其次是可见光，这是一种连续的颜色分布，其中红色为 700 纳米，橙色、黄色（600 纳米），绿色、蓝色（500 纳米），紫色（400 纳米）。 分布以紫外线结束，紫外线从可见光线延伸到大约 300 纳米。
    图\(\PageIndex{2}\)：尽管彩虹与六种颜色 有关，但彩虹是根据波长连续 分布的颜色。

    任何类型的波都可能表现出色散。 例如，声 波、所有类型的电磁波和水波可以根据波长进行 分散。 分散可能需要特殊 环境，并可能产生壮观的显示效果，例如彩虹的 产生。 声音也是如此，因为所有 频率通常都以相同的速度传播。 如果您通过长管（例如吸尘器软管）听到 声音，则可以 很容易地听到声音通过与管道的相互作用而散开。 实际上，色散可以充分揭示波长分散 所遇到的情况。 例如，来自外太空的 电磁辐射的分散已经 揭示了恒星之间存在的事物——所谓的 星际介质。

    尼克·摩尔的视频讨论了他敲击 长弹簧时脉冲的分散。 在摩尔重播显示高频波超过低频 波的高速 镜头时，请听从他的解释。 https://www.youtube.com/watch?v=KbmOcT5sX7I

    在彩虹和许多 其他情况下，折射是分散的原因。 正如我们从斯内尔定律中知道的那样， 折射角度取决于折射率。 我们知道 折射率 n 取决于介质。 但是对于给定的 介质，n 也取决于波长（表 \(\PageIndex{1}\)）。

    表\(\PageIndex{1}\)：不同波长下 选定介质中的折射率 (\(n\))
    中等 红色 (660 纳米) 橙色 (610 纳米) 黄色 (580 纳米) 绿色（550 纳米） 蓝色（470 纳米） 紫罗兰 (410 纳米)
    水 1.331 1.332 1.333 1.335 1.338 1.342
    钻石 2.410 2.415 2.417 2.426 2.444 2.458
    玻璃、皇冠 1.512 1.514 1.518 1.519 1.524 1.530
    玻璃、火石 1.662 1.665 1.667 1.674 1.684 1.698
    聚苯乙烯 1.488 1.490 1.492 1.493 1.499 1.506
    石英，熔融石英 1.455 1.456 1.458 1.459 1.462 1.468

    请注意，对于给定的介质，n 随着波长的 减小而增加，紫光最大。 因此，紫光比红光 弯曲得更多，如图中的棱镜所示 \(\PageIndex{3b}\)。 白光分散到与图\(\PageIndex{1}\)和图中所示相同的波长序列 中 \(\PageIndex{2}\)。

    图 a 显示了三角形玻璃棱镜的图和落在其上并在棱镜两侧折射的纯波长 lambda 入射光。 入射光线击中进入棱镜的弯道。 折射的光线平行于棱镜的底部，然后在另一个表面折射后出现。 由于发生折射的两个表面的法线彼此成一定角度，因此最终效果是每次折射都会使光线弯曲得更远地偏离其原始方向。 图 b 显示了相同的三角棱镜和落在其上的入射白光。 在第一个表面显示了两条折射的光线，分离角度略有不同。 折射的光线落在第二个表面时，会以不同的折射角度折射。 当光线从棱镜中冒出时，会产生760纳米到紫色的红色序列，为380纳米。
    图\(\PageIndex{3}\)：(a) 纯波长的 光落在棱镜上并在两个表面折射。 (b) 白光由棱镜分散（夸大显示）。 由于 折射率随波长而变化，因此 折射角度随波长而变化。 由于折射率随着波长的 减小而稳步增加，因此会 产生从红色到紫色的序列。

    示例\(\PageIndex{1}\)：火石玻璃对白 光的分散

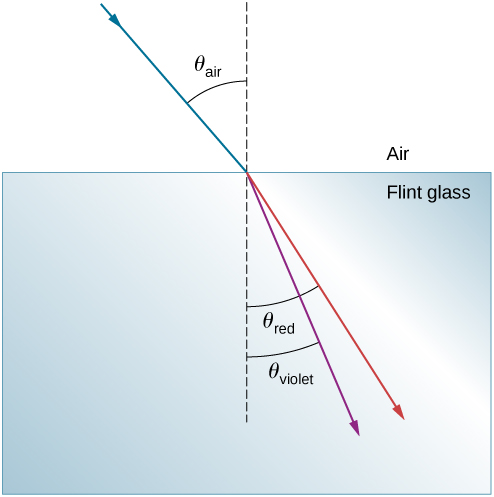
    一束白光以43.2°的入 射角从空气进入火石玻璃。 折射光的红色（660 nm）和紫色（410 nm）部分之间的角度是多少？

    CNX_UPhysics_34_05_FlintGRefr_img.jpg

    策略

    表中列出了不同 波长下火石玻璃的折射指数值\(\PageIndex{1}\)。 使用这些值 计算每种颜色的折射角度，然后取 差值找出色散角。

    解决方案

    对光束的红色部分应用折射定律

    \[n_{air}\sin θ_{air}=n_{red} \sinθ_{red}, \nonumber \]

    我们可以将折射角求解为

    \ [_ {red} =\ sin^ {−1} (\ frac {n_ {air}\ sin 钍_ {air}} {n_ {red}}) =\ sin^ {−1} [\ frac {(1.000)\ sin43.2°} {(1.512)}] =27.0°。 \ nonnumber\]

    同样， 光束紫色部分的入射角为

    \[θ_{violet}=\sin^{−1}(\frac{n_{air}sinθ_{air}}{n_{violet}})=\sin^{−1}[\frac{(1.000)\sin43.2°}{(1.530)}]=26.4°. \nonumber \]

    这两个角度之间的区别是

    \[θ_{red}−θ_{violet}=27.0°−26.4°=0.6°. \nonumber \]

    意义

    尽管 0.6° 看起来似乎是一个可以忽略不计的小角度，但如果允许该 光束传播足够长的距离，则颜色的分散 会变得非常明显。

    练习\(\PageIndex{1}\)

    在前面的例子中，红色和紫色光线在 火石玻璃块内必须 前进多长距离才能分开 1.0 mm？

    回答

    9.3 厘米

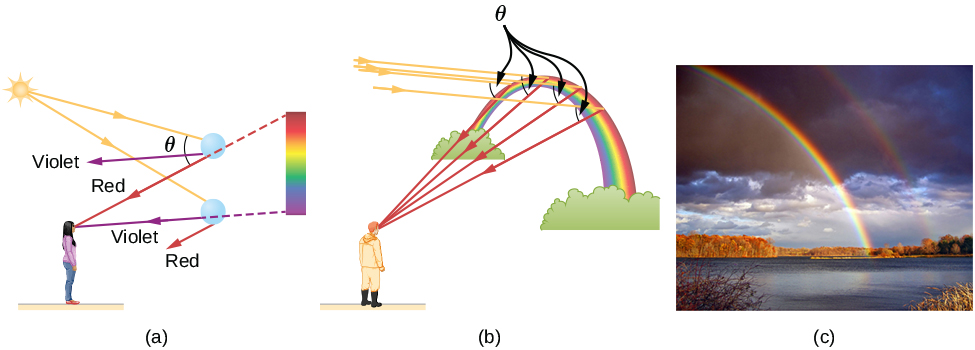
    彩虹是由折 射和反射相结合产生的。 你可能已经注意到，只有当你把目光从太阳移开时， 你才会看到彩虹。 光线进入一滴水并从水滴的背面 反射（图\(\PageIndex{4}\)）。

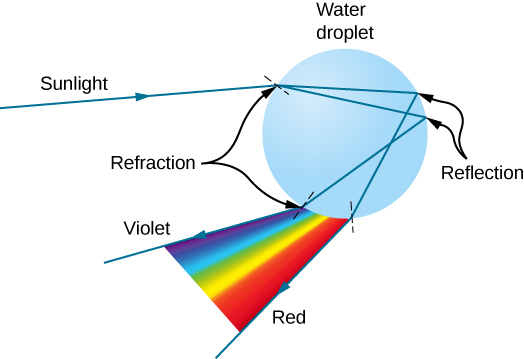
    入射在球形水滴上的太阳光会以不同的角度折射。 折射后的光线会进一步经历完全的内部反射，并在离开水滴时再次折射。 结果，射出的光线会形成从紫色到红色的一系列颜色。 出射的光线与入射的阳光位于水滴的同一侧。
    图\(\PageIndex{4}\)：落 在这个水滴上的光线进入水滴并从水滴的背面反射出来。 这种光在进入和 离开水滴时都会被折射和分散。

    光线在进入和离开 水滴时都会被折射。 由于水的折射率随 波长而变化，因此光线分散，可以观察到彩虹 （图\(\PageIndex{4a}\)）。 （背 面不会出现色散，因为反射定律不取决于 波长。） 观察者看到的实际彩虹色 取决于无数的水滴向 观察者的眼睛折射和反射的无数光线。 当背景较暗时（如暴风雨天气），效果最为 壮观，但也 可以在瀑布和草坪洒水器中观察到。 彩虹 的弧线源于需要以 相对于太阳方向的特定角度观察，如图所示 \(\PageIndex{4b}\)。 如果 水滴中出现两次光反射，则会产生另一个 “次要” 彩虹。 这种罕见 事件产生的弧线位于主彩虹弧线上方，如 图所示\(\PageIndex{4c}\)，并以与主彩虹相反的 顺序生成颜色，最低角度为红色，最大角度为 紫色。

    在图 a 中，阳光照射在两个彼此靠近的水滴上。 入射光线会经历折射和全内反射。 红光从上面的水滴中冒出来，与阳光射线的原始方向形成一个角度 theta。 紫光以较小的角度出现。 红色和紫罗兰色也以略有不同的角度从下部的液滴中冒出。 一个女人背对着太阳，面对水滴，从远处观察。 来自上方液滴的红色和来自下部液滴的紫罗兰从不同的方向到达观察者的眼睛。 观察者看到一条色带，底部为紫罗兰色，顶部为红色。 在图 b 中，一个人看着彩虹，彩虹呈弧形。 来自人体后面的平行光线以不同的位置落在彩虹的外侧，反射和折射，然后到达观察者，每条射线与入射射线形成相同的角度 theta。 到达观察者的光线是红色的。 图 c 显示了天空中双彩虹的照片。
    图\(\PageIndex{5}\)：（a）不同的颜色 出现在不同的方向上，因此你必须看不同的 位置才能看到彩虹的各种颜色。 (b) 彩虹的弧线源于这样一个事实，即观察者与弧线上 任何点之间的直线必须与平行的阳光光 线形成正确的角度，观察者才能接收折射的光线。 (c) 双彩虹。 （来源 c： “Nicholas” /Wikimedia Commons 对作品的修改）

    色散可能会产生美丽的彩虹，但它可能会导致光学系统 出现问题。 用于在光纤 中传输消息的白光是分散的，会随着时间的推移而扩散，最终与其他消息 重叠。 由于激光产生的波长几乎是 纯净的，因此它的光几乎没有色散，这在信息传输方面比白光更具 优势。 相 比之下，从 外层空间进入我们的电磁波的散射可以用来确定它们通过的 物质量。