1.4: 折射

Last updated
Save as PDF

Page ID: 202094

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

在本节结束时，您将能够：

描述光线进入介质后如何改变方向
在解决问题时应用折射定律

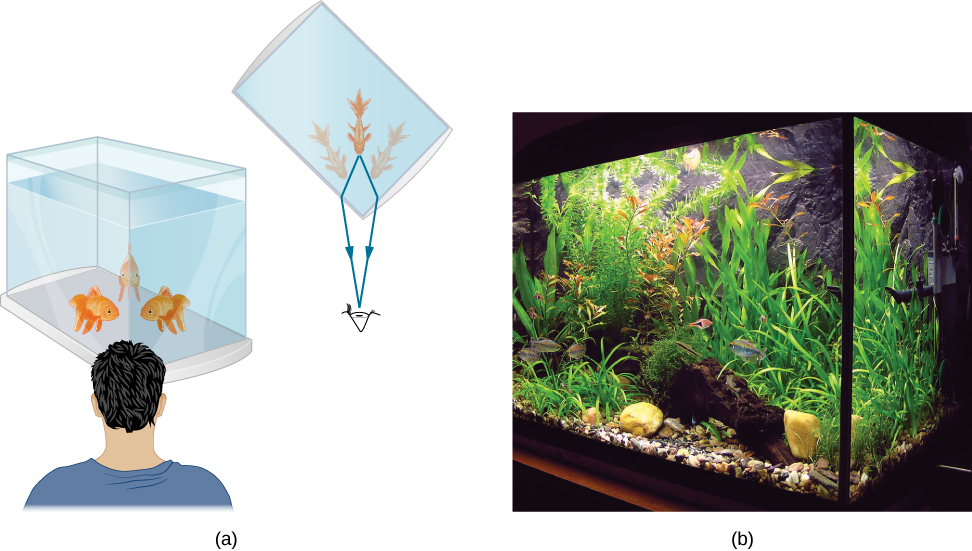
看着鱼缸时，你可能经常会注意到一些奇怪的事情。例如，你可能会看到同一条鱼出现在两个不同的地方（图\(\PageIndex{1}\)）。之所以发生这种情况，是因为来自鱼的光线在离开水箱时会改变方向，在这种情况下，它可以通过两条不同的路径到达你的眼睛。 当光线穿过折射率不同的物质时，光线的方向（粗略地称为弯曲）的变化称为折射，与光速的变化有关\(v=c/n\)。 折射是造成各种光学现象的原因，从镜头的作用到通过光纤传输数据。

图 a 显示了一个人看着鱼缸角落的画作。角落里的一条鱼显示为鱼的双图，其中一张图像是由光线穿过水箱角落的两侧相交而成。图 b 显示了类似情况的照片。 — 图\(\PageIndex{1}\)：（a）观察如图所示的鱼缸，我们可以在两个不同的位置看到相同的鱼，因为光线从水流向空中时会改变方向。在这种情况下，光线可以通过两条不同的路径到达观察者，因此鱼似乎在两个不同的地方。这种光的弯曲称为折射，是造成许多光学现象的原因。 (b) 这张照片显示了鱼缸顶部附近来自鱼的光的折射。

\(\PageIndex{2}\)该图显示了光线从一种介质传递到另一种介质时如何改变方向。和以前一样，角度是在光线穿过表面处相对于垂直于表面的角度进行测量的。（有些入射光是从表面反射的，但现在我们专注于透射的光。）光线方向的变化取决于所涉及的两种介质的折射指数的相对值。在所示情况下，中等 2 的折射率比中等 1 大。请注意，如图所示\(\PageIndex{1a}\)，当光线从折射率较低的介质发展到折射率较高的介质时，光线的方向会更接近垂直线。相反，如图所示\(\PageIndex{1b}\)，当光线从折射率较高的介质发展到折射率较低的介质时，光线的方向会偏离垂直线。这条路径是完全可逆的。

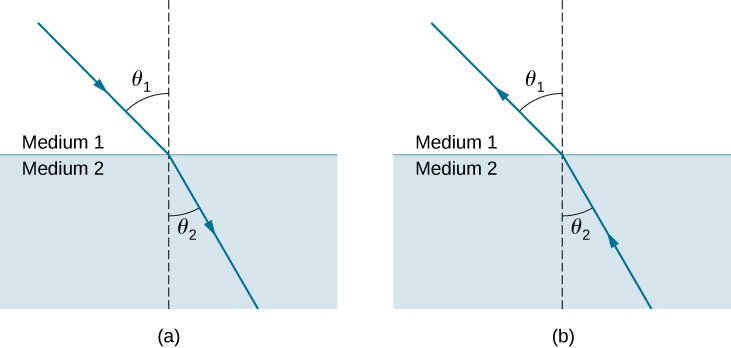
该图说明了光在两个介质之间的界面处的折射情况。在这两幅图中，介质 1 高于介质 2，界面是水平的，并且在界面处绘制了一条折射的射线。在入射点画一条垂直于界面的直线。在图 a 中，光从上方入射，从中等 1 传递到中等 2。在介质 1 中，入射光线与垂直线成一个 theta 的角度，中等 2 中的折射光线与垂直线形成一个较小的角度 theta 2。在图 b 中，光从下方入射，从中等 2 传递到中等 1。在 medium 2 中，入射光线与垂直线成一个 theta 2 的角度，而介质 1 中的折射光线与垂直线形成一个更大的角度 theta 1。图 a 中的 theta one 等于图 b 中的 theta one 角度。同样，图 a 中的 theta two 等于图 b 中的 theta two 角度。 — 图\(\PageIndex{2}\)：光线方向的变化取决于光线从一种介质穿过另一种介质时的折射率如何变化。在此处所示的情形中，介质 2 的折射率大于中等 1 中的折射率。 (a) 当光线进入折射率较高的介质时，光线会靠近垂直线。 (b) 当光线进入折射率较低的介质时，光线会从垂直线移开。

光线改变方向的量既取决于入射角度，也取决于速度的变化量。对于给定入射角度的射线，速度的巨大变化会导致方向的巨大变化，从而导致角度的巨大变化。确切的数学关系是折射定律或斯内尔定律，继荷兰数学家威勒布罗德·斯内尔（1591-1626 年）之后，他在1621年发现了折射定律。折射定律以方程形式表示为

\[n_1 \, \sin \, θ_1=n_2 \, \sin \, θ_2. \label{snell's law} \]

这里 (n_1\) 和\(n_2\)是介质 1 和 2 的折射指数，\(θ_1\)和\(θ_2\)是介质 1 和 2 中光线与垂直线之间的角度。入射射线称为入射射线，传出射射线称为折射射线，关联角度分别为入射角和折射角度。

斯内尔的实验表明，折射定律得到遵守，\(n\)可以为给定介质分配特征折射率并测量其值。斯内尔没有意识到光速在不同的介质中会有所不同，这是我们在理论上使用惠更斯原理得出折射定律时使用的关键事实。

示例\(\PageIndex{1}\): Determining the Index of Refraction

假设介质 1 是空气\(\PageIndex{1a}\)，并假设入射角为 30.0°，折射角为 22.0°，在图中找出介质 2 的折射率。

策略

在大多数情况下，空气的折射率被视为 1（最多四个有效数字，为 1.000）。因此，\(n_1=1.00\)在这里。根据给定的信息，\(θ_1=30.0°\)以及\(θ_2=22.0°\)。有了这些信息，斯内尔定律中唯一的未知数就是\(n_2\)，因此我们可以使用斯内尔定律（方程\ ref {snell 定律}）来找到它。

解决方案

根据斯内尔定律（方程\ ref {snell 定律}），我们有

\[\begin{align*} n_1\sin θ_1 &=n_2 \sin θ_2 \\[4pt] n_2 &= n_1\dfrac{\sin θ_1}{\sin θ_2}. \end{align*} \nonumber \]

输入已知值，

\[\begin{align*} n_2 &=1.00 \dfrac{\sin 30.0°}{\sin 22.0°} \\[4pt] &= \dfrac{0.500}{0.375} \\[4pt] &=1.33. \end{align*} \nonumber \]

意义

这是水的折射率，斯内尔本可以通过测量角度并进行此计算来确定它。然后他就会发现，在所有其他情况下，例如当光线从水传递到玻璃时，1.33是水的合适折射率。今天，我们可以通过直接测量光速来验证折射率与介质中的光速有关。

探索具有不同折射率的两种介质之间的光线弯曲。使用 “简介” 模拟，看看从空气变为水再到玻璃如何改变弯曲角度。使用量角器工具测量角度，看看是否可以在示例中重新创建配置\(\PageIndex{1}\)。另外，通过测量，确认反射角等于入射角。

示例\(\PageIndex{2}\): A Larger Change in Direction

假设在示例中这样的情况下\(\PageIndex{1}\)，光从空气流向金刚石，入射角为 30.0°。计算钻石中的折射角度 β ₂。

策略

再说一遍，空气的折射率被假定为 n ₁ =1.00，我们得到 β ₁ =30.0°。我们可以查看钻石的折射率，发现 n ₂ =2.419。斯内尔定律中唯一的未知\(θ_2\)数是，我们希望予以确定。

解决方案

求解斯内尔定律（方程\ ref {snell 定律}）以获得\(\sin θ_2\)收益率

\[\sin θ_2=\frac{n_1}{n_2}\sin θ_1. \nonumber \]

输入已知值，

\[\sin θ_2=\frac{1.00}{2.419}\sin30.0°=(0.413)(0.500)=0.207. \nonumber \]

角度是这样的

\[θ_2=\sin^{−1}(0.207)=11.9°. \nonumber \]

意义

对于相同的 30.0° 入射角，金刚石的折射角明显小于水中的折射角度（11.9° 而不是 22.0° ——参见示例\(\PageIndex{2}\)）。这意味着钻石的方向有更大的变化。方向变化较大的原因是折射率（或速度）的巨大变化。通常，速度变化越大，对射线方向的影响就越大。

练习\(\PageIndex{1}\): Zircon

折射率仅次于钻石的固体是锆石。如果示例中的钻石\(\PageIndex{2}\)被一块锆石所取代，那么新的折射角度会是多少？

回答: 15.1°