18.16：Waves

$检查你的理解

16.1。 波浪的波长取决于波浪的频率和速度。 声波的频率等于弦上波浪的频率。 只有在波浪的速度相同时，声波的波长和弦上的波长才相等，但情况并非总是如此。 如果声波的速度与弦上波浪的速度不同，则波长是不同的。 声波的这种速度将在 “声音” 中讨论。

16.2。 在横向波中，波浪可能以恒定的传播速度在介质中移动，但介质会垂直于波浪的运动振荡。 如果波浪沿正 x 方向移动，则介质会在 y 方向上下振荡。 因此，介质的速度不是恒定的，但是介质的速度和加速度与弹簧上质量的简单谐波运动的速度和加速度相似。

16.3。 是的，余弦函数等于具有相移的正弦函数，任何一个函数都可以在波函数中使用。 哪个函数更方便使用取决于初始条件。 在图 16.11 中，波浪的初始高度为 y (0.00, 0.00) = 0，然后波浪高度增加到波峰处的最大高度。 如果初始时间的初始高度等于波浪的振幅 y (0.00, 0.00) = +A，则使用余弦函数对波浪进行建模可能更方便。

16.4。 该波的振幅 A = 0.5 m，波长$\lambda$ = 10.00 m，周期 T = 0.50 s，是波速 v = 20.00 m/s 的波动方程的解。

16.5。 由于嘲讽弦上波浪的速度与张力的平方根除以线性密度成正比，因此波速将增加$\sqrt{2}$。

16.6。 乍一看，正弦波在弦上的时间平均功率可能与弦的线性密度成正比，因为 P =$\frac{1}{2} \mu$ A ²$\omega^{2}$ v；但是，波的速度取决于线性密度。 将波速替换为$\sqrt{\frac{F_{T}}{\mu}}$表示功率与张力的平方根成正比，与线性质量密度的平方根成正比： $$P = \frac{1}{2} \mu A^{2} \omega^{2} v = \frac{1}{2} \mu A^{2} \omega^{2} \sqrt{\frac{F_{T}}{\mu}} = \frac{1}{2} A^{2} \omega^{2} \sqrt{\mu F_{T}} \ldotp$$

16.7。 是的，这些方程同样适用于介质的对称边界条件，两端都有反向节点，两端都有反向点。 前三种模式的正常模式如下所示。 虚线显示介质的平衡位置。

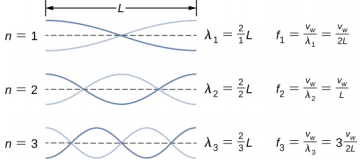
请注意，第一种模式是波长的四分之二或一半。 第二种模式是四分之一的波长，然后是波长的一半，然后是四分之一的波长或一个完整波长。 第三种模式是一个半波长。 这些结果与两端各有一个节点的字符串的结果相同。 对称边界条件的方程同样适用于固定边界条件和自由边界条件。 下一章在讨论开放式管道中的声波时，将重新审视这些结果。

概念性问题

1。 吉他弦上的波浪就是横向波浪的一个例子。 弦的扰动垂直于波浪的传播移动。 弦乐产生的声音是一种纵波，其中空气的干扰与波浪的传播平行移动。

3。 传播速度是波浪在介质中传播的速度。 如果波速恒定，则速度可通过 v =$\frac{\lambda}{T}$ =$\lambda$ f 得出。频率是单位时间内通过一个点的波浪数。 波长与波速成正比，与频率成反比。

5。 不，你上下移动手的距离将决定波浪的振幅。 波长将取决于你上下移动手的频率，以及波浪穿过弹簧的速度。

7。 来自太阳和恒星的光通过空旷的空间到达地球，那里没有媒介存在。

9。 波长等于波速乘以频率，波数等于 k =$\frac{2 \pi}{\lambda}$，所以是的，波数将取决于频率，也取决于波浪在弹簧中传播的速度。

11。 当波浪通过介质传播时，介质以简单的谐波运动移动，速度不断变化，因此会加速。 介质的加速归因于介质的恢复力，其作用方向与位移方向相反。

13。 波速与张力的平方根成正比，因此速度翻了一番。

15。 由于弦上波浪的速度与线性质量密度的平方根成反比，因此在弦的低线性质量密度下，速度会更高。

17。 电线中的张力是由于电力电缆的重量造成的。

19。 时间平均功率为 P$\frac{E_{\lambda}}{T}$ =$\frac{1}{2} \mu$ A ²$\omega^{2} \frac{\lambda}{T} = \frac{1}{2} \mu$ A ²$\omega^{2}$ v。如果频率或振幅减半，则功率将降低 4 倍。

21。 当弦上的一部分垂直移动时，它会对弦的相邻部分施加力，对该部分起作用并传递能量。

23。 球形波的强度为 I =$\frac{P}{4 \pi r^{2}}$，如果没有消耗能量，则三米处的强度将降低九倍。

25。 在接口处，入射脉冲产生反射脉冲和发射脉冲。 反射脉冲相对于入射脉冲将异相，并将以与入射脉冲相同的传播速度移动，但会朝相反的方向移动。 发射的脉冲将沿着与入射脉冲相同的方向传播，但速度只有一半。 发射的脉冲将与入射脉冲同相。 反射脉冲和发射脉冲的振幅都将小于入射脉冲的振幅。

27。

29。 这可能就像少量改变长度和/或密度一样简单，这样零件就不会在电动机的频率下产生共振。

31。 能量是通过用手指在玻璃上施加力量完成的工作为玻璃提供的。 当以正确的频率供电时，会形成驻波。 玻璃产生共鸣，振动产生声音。

33。 对于方程 y (x, t) = 4.00 cm sin (3 m ⁻¹ x) cos (4 s ⁻¹ t)，有一个节点，因为当 x = 0.00 m 时，sin (3 m ⁻¹ (0.00 m)) = 0.00，所以 y (0.00 m，t) = 0.00 m。 对于方程 y (x, t) = 4.00 cm sin (3 m ⁻¹ x +$\frac{\pi}{2}$) cos (4 s ⁻¹ t)，存在反向节点，因为当 x = 0.00 m 时，sin (3 m ⁻¹ (0.00 m$\frac{\pi}{2}$) +) = + 1.00，所以 y (0.00 m, t) 在余弦项在 +1 和 -1 之间振荡。

问题

35。 2d = vt$\Rightarrow$ d = 11.25 m

37。 v = f$\lambda$，所以 f = 0.125 Hz，所以 N = 7.50 倍

39。 v = f$\lambda \Rightarrow \lambda$ = 0.400 m

41。 v = f$\lambda \Rightarrow$ f = 2.50 x 10 ⁹ Hz

43。 a. P 波以 v = 3.20 km/s 的速度超过 S 波；因此，$\Delta$d = 0.320 km。

b. 由于距离的不确定性小于一公里，我们对第 (a) 部分的答复似乎没有限制对核弹爆炸的探测。 但是，如果速度不确定，那么距离的不确定性就会增加，从而可能难以确定地震波的来源。

45。 v = 1900 m/s，$\Delta$t = 1.05$\mu$ 秒

47。 y (x, t) = −0.037 cm

49。 脉冲将移动$\Delta$ x = 6.00 m。

51。 a. A = 0.25 m

b.k = 0.30 m ⁻¹

c.$\omega$ = 0.90 s ⁻¹

d. v = 3.0 m/s

e.$\phi$ =$\frac{\pi}{3}$ rad

f.$\lambda$ = 20.93 m

g. T = 6.98 秒

53。 A = 0.30 m，$\lambda$= 4.50 m，v = 18.00 m/s，f = 4.00 Hz，T = 0.25 秒

55。 y (x, t) = 0.23 m sin (3.49 m ⁻¹ x − 0.63 s ⁻¹ t)

57。 它们具有相同的角频率、频率和周期。 它们朝相反的方向移动，y ₂ (x, t) 的波长是 y ₁ (x, t) 的两倍，并且以波速的一半移动。

59。 介质中的每个粒子在每个周期移动 4A 的距离。 周期可以通过将速度除以波长得出：t = 10.42 s

61。 a.$\mu$ = 0.040 kg/m

b.v = 15.75 m/s

63。 v = 180 m/s

65. v = 547.723 ms，$\Delta$t = 5.48 毫秒

67。 v _s = 347.56 m/s

69。 v ₁ t + v ₂ t = 2.00 m，t = 1.69 毫秒

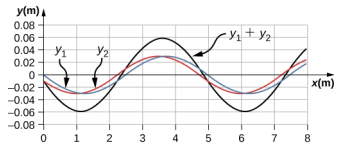
71。 v = 288.68 m/s，$\lambda$= 0.73 m

73。 a. A = 0.0125 厘米

b. F _T = 0.96 N

75。 v = 74.54 m/s，$P_{\lambda}$= 91.85 W

77。 I = 20.0 W/m ²

b. I =$\frac{P}{A}$，A = 10.0 m2 A = 4$\pi$ r ²，r = 0.892 m

79。 I = 650 W/m ²

81。 $$P \propto E \propto I \propto X^{2} \Rightarrow \frac{P_{2}}{P_{1}} = \left(\dfrac{X_{2}}{X_{1}}\right)^{2}$$

P ₂ = 2.50 kW

83。 $$I \propto X^{2} \Rightarrow \frac{I_{1}}{I_{2}} = \left(\dfrac{X_{1}}{X_{2}}\right)^{2}$$

I ₂ = 3.38 x 10 ⁻⁵ W/m ²

85。 f = 100.00 Hz，A = 1.10 厘米

87。 a. I ₂ = 0.063I ₁

b. I ₁ 4$\pi$ r ₁ ² = I ₂ 4$\pi$ r ₂ ²，r ₂ = 3.16 m

89。 2$\pi$ r ₁ A ₁ ² = 2$\pi$ r ₂ A ₂ ²、A ₁ =$\left(\dfrac{r_{2}}{r_{1}}\right)^{1/2}$、A ₁ = 0.17 m

91。 y (x, t) = 0.76 m

93。 A _R = 2A cos$\left(\dfrac{\phi}{2}\right)$，$\phi$= 1.17 rad

95。 y _R = 1.90 厘米

97。 $\omega$= 6.28 s ⁻¹，k = 3.00 m ⁻¹，$\phi$=$\frac{\pi}{8}$ rad，A _R = 2A cos$\left(\dfrac{\phi}{2}\right)$，A = 0.37 m

99。 一个。

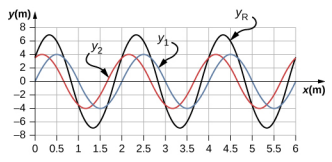
b.$\lambda$ = 2.0 m，A = 4 m

c.$\lambda_{R}$ = 2.0 m，A _R = 6.93 m

101。 y _R (x, t) = 2A cos c$\left(\dfrac{\phi}{2}\right)$ os$\left(kx − \omega t + \dfrac{\phi}{2}\right)$; 结果并不奇怪，因为 cos ($\theta$) = sin ($\theta + \frac{\pi}{2}$)。

103。 $$\begin{split} \lambda_{n} & = \frac{2.00}{n} L, \quad f_{n} = \frac{v}{\lambda_{n}} \\ \lambda_{1} & = 4.00\; m, \quad f_{1} = 12.5\; Hz \\ \lambda_{2} & = 2.00\; m, \quad f_{2} = 25.00\; Hz \\ \lambda_{3} & = 1.33\; m, \quad f_{3} = 37.59\; Hz \end{split}$$

105。 v = 158.11 m/s，$\lambda$= 4.44 m，f = 35.61 Hz，$\lambda_{s}$= 9.63 m

107。 y (x, t) = [0.60 cm sin (3 m ⁻¹ x)] cos (4 s ⁻¹ t)

109。 $$\begin{split} \lambda_{100} & = 0.06\; m \\ v & = 56.8\; m/s, \quad f_{n} = n f_{1}, \quad n = 1, 2, 3, 4, 5 \ldots \\ f_{100} & = 947\; Hz \end{split}$$

111。 T = 2$\Delta$ t、v =$\frac{\lambda}{T}$、$\lambda$ = 2.12 m

113。 $\lambda_{1}$= 6.00 m，$\lambda_{2}$= 3.00 m，$\lambda_{3}$= 2.00 m，$\lambda_{4}$= 1.50 m；v = 258.20 m/s =$\lambda$ f；f ₁ = 43.03 Hz，f ₂ = 86.07 Hz，f ₃ = 129.10 Hz，f ₄ = 172.13 Hz

115。 v = 134.16 ms，$\lambda$= 1.4 m，f = 95.83 Hz，T = 0.0104 秒

其他问题

117。 $\lambda$= 0.10 m

119。 a.f = 4.74 x 10 ¹⁴ Hz

b.$\lambda$ = 422 nm

121。 $\lambda$= 16.00 m，f = 0.10 Hz，T = 10.00 秒，v = 1.6 m/s

123。 $\lambda$= (v _b + v) t _b，v = 3.75 m/s，$\lambda$= 3.00 m

125。 $$\begin{split} \frac{\partial^{2} (y_{1} + y_{2})}{\partial t^{2}} & = -A \omega^{2} \sin (kx - \omega t) - A \omega^{2} \sin (kx - \omega t + \phi) \\ \frac{\partial^{2} (y_{1} + y_{2})}{\partial x^{2}} & = -Ak^{2} \sin (kx - \omega t) - Ak^{2} \sin (kx - \omega t + \phi) \\ \frac{\partial^{2} y(x,t)}{\partial x^{2}} & = \frac{1}{v^{2}} \frac{\partial^{2} y(x,t)}{\partial t^{2}} \\ -A \omega^{2} \sin (kx - \omega t) - A \omega^{2} \sin (kx - \omega t + \phi) & = \left(\dfrac{1}{v^{2}}\right) (-Ak^{2} \sin (kx - \omega t) - Ak^{2} \sin (kx - \omega t + \phi)) \\ v & = \frac{\omega}{k} \end{split}$$

127。 y (x, t) = 0.40 m sin (0.015 m ⁻¹ x + 1.5 s ⁻¹ t)

129。 v = 223.61 m/s，k = 1.57 m ⁻¹，$\omega$= 142.43 s ⁻¹

131。 P =$\frac{1}{2}$ A ² (2$\pi$ f) ²$\sqrt{\mu F_{T}}$，$\mu$= 2.00 x 10 ⁻⁴ kg/m

133。 P =$\frac{1}{2} \mu$ A ²$\omega^{2} \frac{\lambda}{T}$，$\mu$= 0.0018 kg/m

135。 a. A _R = 2A cos$\left(\dfrac{\phi}{2}\right)$，cos$\left(\dfrac{\phi}{2}\right)$$\phi$ = 1，= 0$\pi$、2$\pi$、4...

b. A _R = 2A cos$\left(\dfrac{\phi}{2}\right)$，cos$\left(\dfrac{\phi}{2}\right)$$\phi$ = 0，= 0$\pi$，3$\pi$，5\ (\ pi)，...

137。 y _R (x, t) = 0.6 m sin (4 m ⁻¹) cos (3 s ⁻¹ t)

139。 一个。 $$\begin{split} &F_{T} - 20.00\; kg(9.80\; m/s^{2}) \cos 45^{o} & = 0 \\ &m(9.80\; m/s^{2}) - F_{T} = 0 \\ &m = 14.14\; kg \end{split}$$

b. F _T = 138.57 N，v = 74.45 m/s

141。 F _T = 2 N，v = 6.73 m/s

143。 a.f _n =$\frac{nv}{2L}$、v =$\frac{2L f_{n + 1}}{n + 1}$$\frac{n + 1}{n} = \frac{2L f_{n + 1}}{2L f_{n}}$、1 +$\frac{1}{n}$ = 1.2、n = 5；$\lambda_{n}$=$\frac{2}{n}$ L、$\lambda_{5}$ = 1.6 m、$\lambda_{6}$ = 1.33 m

b. F _T = 245.76 N

挑战问题

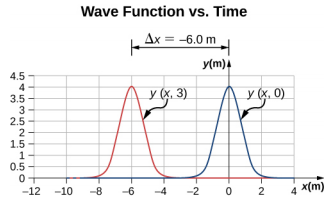
145。 a. 以 v = 2.00 m/s 的传播速度向负 x 方向移动。

b.$\Delta$ x = −6.00 m

c。

147。 $$\begin{split} \sin(kx - \omega t) & = \sin \left(kx + \dfrac{\phi}{2}\right) \cos \left(\omega t + \dfrac{\phi}{2}\right) - \cos \left(kx + \dfrac{\phi}{2}\right) \sin \left(\omega t + \dfrac{\phi}{2}\right) \\ \sin(kx - \omega t + \phi) & = \sin \left(kx + \dfrac{\phi}{2}\right) \cos \left(\omega t + \dfrac{\phi}{2}\right) + \cos \left(kx + \dfrac{\phi}{2}\right) \sin \left(\omega t + \dfrac{\phi}{2}\right) \\ \sin(kx - \omega t) + \sin(kx - \omega t + \phi) & = 2 \sin \left(kx + \dfrac{\phi}{2}\right) \cos \left(\omega t + \frac{\phi}{2}\right) \\ y_{R} & = 2A \sin \left(kx + \frac{\phi}{2}\right) \cos \left(\omega t + \dfrac{\phi}{2}\right) \end{split}$$

149。 sin$\left(kx + \dfrac{\phi}{2}\right)$ = 0、kx +$\frac{\phi}{2}$ = 0$\pi$、2$\pi$、1.26 m ⁻¹ x +$\frac{\pi}{20}$ =$\pi$、2$\pi$、3$\pi$；x = 2.37 m、4.86 m、7.35 m

贡献者和归因

Template:ContribOpenStaxUni