18.10：固定轴旋转简介

Last updated
Save as PDF

Page ID: 204470

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

检查你的理解

10.1。 a. 40.0 rev/s = 2$pi$ (40.0) rad/s，$\bar{\alpha} = \frac{\Delta \omega}{\Delta t} = \frac{2 \pi (40.0) − 0\; rad/s}{20.0\; s}$= 2$\pi$ (2.0) = 4.0$\pi$ rad/s ²

b. 由于角速度呈线性增加，因此在整个指定时间内必须保持恒定的加速度。因此，任何时候的瞬时角加速度都是 4.0$\pi$ rad/s ² 的解。

10.2。 a. 使用方程 10.25，我们有 7000 rpm$\frac{7000.0(2 \pi\; rad)}{60.0\; s}$ = = 733.0 rad/s，$$\ alpha =\ frac {\ omega_ {0}} {t} =\ frac {733.0\; rad/s} = 73.3\; rad/s^ {2}\]

b. 使用方程 10.29，我们有 $$\ omega^ {2} =\ omega_ {0} ^ {2} + 2\ alpha\ Delta\ theta\ Rightarrow\ Delta\ theta =\ frac {\ theta =\ frac {0\; rad/s ^ {2}} {2 (73.3\; rad/s^ {2})} = 3665.2\; rad\]

10.3。 角加速度为$\alpha = \frac{(5.0 − 0)\; rad/s}{20.0\; s}$ = 0.25 rad/s ²。因此，男孩穿过的总角度为 $$\ Delta\ theta =\ frac {\ omega^ {2}-\ omega_ {0} ^ {2}} {2\ alpha} =\ frac {(5.0) ^ {2}-0} {2 (0.25)} = 50\; rad$$thus，我们计算 $$s = r\ theta = (5.0\; m) (50.0\; rad) = 250.0\; m\]

10.4。 螺旋桨的初始旋转动能为 $$K_ {0} =\ frac {1} {2} I\ omega^ {2} =\ frac {1} {2} (800.0\; kg\ cdotp m^ {2}) ^ {2} = 2.53\ times 10^ {5}\; J ldotp$$at 5.0 s 螺旋桨的新旋转动能是 $$K_ {f} = 2.03\ times 10^ {5}\; J\ ldotp$and新的角速度是 $$\ omega =\ sqrt {\ frac {2 (2.03\ times 10^ {5}\; J)} {800.0\; kg\ cdotp m^ {2}}} = 22.53\; rad/s$$即 3.58 rev/s。

10.5。 我_平行轴 = I _质心 + md ² = mR ² + mR ² = 2mR ²

10.6。 杠杆臂和力向量之间的角度为 80°；因此，r _$\perp$= 100 m（sin 80°）= 98.5 m。横积$\vec{\tau} = \vec{r} \times \vec{F}$给出负扭矩或顺时针扭矩。然后$\tau = - r_{\perp} F$扭矩为 −98.5 m（5.0 x 10 ⁵ N）= −4.9 x 10 ⁷ N • m。

10.7。 a. 角加速度为$\alpha = \frac{20.0(2 \pi)\; rad/s − 0}{10.0 \; s}$ = 12.56 rad/s ²。求解扭矩，我们有$\sum_{i} \tau_{i} = I \alpha$ = (30.0 kg • m ²) (12.56 rad/s ²) = 376.80 N • m

b. 角加速度为$\alpha = \frac{0 − 20.0(2 \pi)\; rad/s}{20.0\; s}$ = −6.28 rad/s ²。求解扭矩，我们有$\sum_{i} \tau_{i} = I \alpha$ = (30.0 kg • m ²) (−6.28 rad/s ²) = −188.50 N • m

10.8。 3 兆瓦

概念性问题

1。秒针顺时针旋转，因此按照右手法则，角速度矢量进入墙壁。

3。它们具有相同的角速度。球棒上距离更远的点的切线速度更快。

5。直线，在时间变量中呈线性

7。常量

9。向心加速度向量垂直于速度矢量。

11。 a. 两者；b. 非零向心加速度；c. 两者

13。 空心球体，因为质量分布在离旋转轴更远的地方。

15。 a. 它减少了。b. 手臂可以用棒近似，铁饼可以用圆盘近似。躯干靠近旋转轴，因此它对惯性矩的影响不大。

17。 因为惯性矩随着到旋转轴距离的平方而变化。距离大于 L/2 的杆的质量将提供更大的贡献，使其惯性矩大于点质量$\frac{L}{2}$。

19。 力的大小、杠杆臂的长度、杠杆臂的角度和力向量

21。 车轮的惯性矩减小，因此需要较小的扭矩来加速车轮。

23。 是的

25。 |$\vec{r}$ | 可以等于杠杆臂，但不能小于杠杆臂

27。 如果力沿着旋转轴线，或者它们具有相同的杠杆臂并且施加在杆上的某个点。

问题

29。 $\omega = \frac{2 \pi\; rad}{45.0\; s}$= 0.14 rad/s

31。 a.$\theta = \frac{s}{r} = \frac{3.0\; m}{1.5\; m}$ = 2.0 rad

b.$\omega = \frac{2.0\; rad}{1.0\; s}$ = 2.0 rad/s

c.$\frac{v^{2}}{r} = \frac{(3.0\; m/s)^{2}}{1.5\; m}$ = 6.0 m/s ².

33。 螺旋桨只需$\Delta$ t$\frac{\Delta \omega}{\alpha} = \frac{0\; rad/s − 10.0(2 \pi)\; rad/s}{−2.0\; rad/s^{2}}$ = 31.4 秒即可休息，当螺旋桨处于 0 rad/s 时，它将开始朝相反的方向旋转。这是不可能的，因为让螺旋桨停止并开始朝相反方向旋转所涉及的力很大。

35。 a.$\omega$ = 25.0 (2.0 s) = 50.0 rad/s

b.$\alpha = \frac{d \omega}{dt}$ = 25.0 rad/s ²

37。 a.$\omega$ = 54.8 rad/s

b.t = 11.0 秒

39。 a. 0.87 rad/s ²

b.$\theta$ = 66,264 rad

41。 a.$\omega$ = 42.0 rad/s

b.$\theta$ = 220 rad

c.v _t = 42 m/s，a _t = 4.0 m/s ²

43。 a.$\omega$ = 7.0 rad/s

b.$\theta$ = 22.5 rad

c.a _t = 0.1 m/s

45。 $\alpha$= 28.6 rad/s ².

47。 r = 0.78 m

49。 a.$\alpha$ = −0.314 rad/s ²

b.a _c = 197.4 m/s ²

c.a$\sqrt{a_{c}^{2} + a_{t}^{2}} = \sqrt{197.4^{2} + (−6.28)^{2}}$ = 197.5 m/s ²，$\theta$= tan ^{−1$\frac{−6.28}{197.4}$ = −1} = −1.8° 从向心加速度向量顺时针方向

51。 ma = 40.0 kg (5.1 m/s ²) = 204.0 N

最大摩擦力为$\mu_{S}$ N = 0.6（40.0 kg）（9.8 m/s ²）= 235.2 N，因此孩子还不会掉下来。

53。 $$\ begin {split} v_ {t} & = r\ omega = 1.0 (2.0t)\; m/s\\ a_ {c} & =\ frac {v_ {t} ^ {2}} =\ frac {(2.0t) ^ {2}\; m/s^ {2}\\ a_ t} (t) & = r\ alpha (t) = r\ frac {d\ omega} {dt} = 1.0\; m (2.0) = 2.0\; m/s^ {2}\ ldotp\ end {split} $$Plotting 两个加速度都给

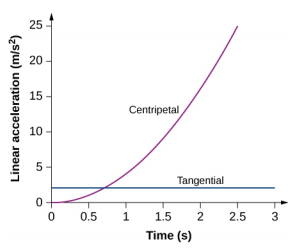
该图显示了以米/秒为单位的线性加速度，以秒为单位的时间函数绘制而成。向心从坐标系的原点开始，并随着时间的推移呈指数增长。切线为正值并随着时间的推移保持不变

切向加速度是恒定的，而向心加速度取决于时间，并且随着时间的推移而增加，其值远大于 t = 1s 之后的切向加速度。对于小于 0.7 秒且接近零的时间，向心加速度远小于切向加速度。

55。 a. K = 2.56 x 10 ²⁹ J

b. K = 2.68 x 10 ³³ J

57。 K = 434.0 J

59。 a.v _f = 86.5 m/s

b. 螺旋桨的旋转速度在 20 转/秒时保持不变。

61。 K = 3.95 x 10 ⁴² J

63。 a. I = 0.315 kg • m ²

b. K = 621.8 J

65。 I =$\frac{7}{36}$ mL ²

67。 v = 7.14 m/s。

69。 $\theta$= 10.2°

71。 F = 30 N

73。 a. 0.85 m (55.0 N) = 46.75 N • m

b. 你推到什么高度都没关系。

75。 m ₂$\frac{4.9\; N \cdotp m}{9.8(0.3\; m)}$ = 1.67 千克

77。 $\tau_{net}$= −9.0 N • m + 3.46 N • m + 0 − 3.28 N • m = −8.82 N • m

79。 $\tau$= 5.66 N • m

81。 $\sum \tau$= 57.82 N • m

83。 $\vec{r} \times \vec{F}$= 4.0$\hat{i}$ + 2.0$\hat{j}$ − 16.0$\hat{k}$ N • m

85。 a.$\tau$ = (0.280 m) (180.0 N) = 50.4 N • m

b.$\alpha$ = 17.14 rad/s ²

c.$\alpha$ = 17.04 rad/s ²

87。 $\tau$= 8.0 N • m

89。 $\tau$= −43.6 N • m

91。 a.$\alpha$ = 1.4 x 10 ⁻¹⁰ rad/s ²

b.$\tau$ = 1.36 x 10 ²⁸ N • m

c. F = 2.1 x 10 ²¹ N

93。 a = 3.6 m/s ²

95。 a.a = r$\alpha$ = 14.7 m/s ²

b.a$\frac{L}{2} \alpha$ =$\frac{3}{4}$ g

97。 $\tau = \frac{P}{\omega} = \frac{2.0 \times 10^{6}\; W}{2.1\; rad/s}$= 9.5 x 10 ⁵ N • m

99。 a. K = 888.50 J

b.$\Delta \theta$ = 294.6 rev

101。 a. I = 114.6 kg • m ²

b. P = 104,700 W

103。 v = L$\omega$ =$\sqrt{3Lg}$

105。 a.a = 5.0 m/s ²

b. W = 1.25 N • m

其他问题

107。 $\Delta$t = 10.0 秒

109。 a. 0.06 rad/s ²

b.$\theta$ = 105.0 rad

111。 s = 405.26 m

113。 a. I = 0.363 kg • m ²

b. I = 2.34 千克 • m ²

115。 $\omega =\sqrt{\frac{5.36\; J}{4.4\; kg \cdotp m^{2}}}$= 1.10 rad/s

117。 F = 23.3 N

119。 $\alpha = \frac{190.0\; N \cdotp m}{2.94\; kg \cdotp m^{2}}$= 64.4 rad/s ²

挑战问题

121。 a.$\omega$ = 2.0t − 1.5t ²

b.$\theta$ = t ² − 0.5t ³

c.$\theta$ = −400.0 rad

d. 向量位于 −0.66 (360°) = −237.6°

123。 I = m$\frac{2}{5}$ R ²

125。 a.$\omega$ = 8.2 rad/s

b.$\omega$ = 8.0 rad/s

贡献者和归因

Template:ContribOpenStaxUni