18.5: 牛顿运动定律
- Page ID
- 204505
检查你的理解
5.1。 14 N, 56° 从 x 轴正向测量
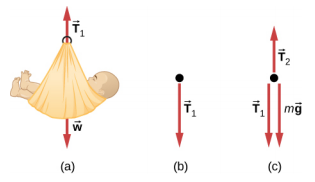
5.2。 a. 他的体重向下起作用,降落伞的空中抵抗力向上起作用。b. 两者都不是;力的大小相等
5.3。 0.1 m/s 2
5.4。 40 m/s 2
5.5。 a. 159.0\(\hat{i}\) + 770.0\(\hat{j}\) N;b. 0.1590\(\hat{i}\) + 0.7700\(\hat{j}\) N
5.6。 a = 2.78 m/s 2
5.7。 a. 3.0 m/s 2;b. 18 N
5.8。 a. 1.7 m/s 2;b. 1.3 m/s 2
5.9。 6.0×10 2 N
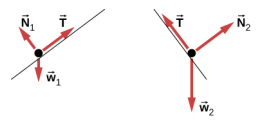
5.10。
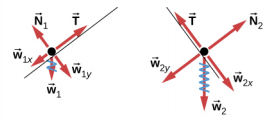
概念性问题
1。 力是定向的,有大小。
3。 刹车动作前的纸杯蛋糕速度与汽车的速度相同。 因此,纸杯蛋糕是运动中不受限制的尸体,当汽车突然停下时,纸杯蛋糕按照牛顿的第一定律不断向前移动。
5。 不。 如果此时力为零,那么就没有什么可以改变物体的瞬间零速度了。 由于我们没有观察到物体一动不动地悬挂在空中,因此力不可能为零。
7。 宇航员在所描述的位置确实失重,因为附近没有大型天体(行星或恒星)可以施加引力。 不管她身在何处,她的体重都是 70 kg。
9。 你施加的力(大小等于你的体重的接触力)很小。 相比之下,地球非常庞大。 因此,地球的加速度将非常小。 要了解这一点,请使用牛顿第二定律来计算如果您的体重为 600.0 N 而地球的质量为 6.00 x 10 24 kg,则会产生的加速度。
11。 a. 行动:地球拉动月球,反应:月球拉动地球;b. 动作:脚对球施加力,反应:球对脚施加力;c. 动作:火箭推动气体,反应:气体向后推火箭;d. 动作:汽车轮胎在路上向后推,反应:轮胎向前推路;e. 行动:跳线向下推地面,反应:地面在跳线上向上推;f. 行动:枪在子弹上向前推动,反应:子弹向后推枪。
13。 a. 步枪(由步枪支撑的炮弹)施加力量驱逐子弹;对这种力的反应是子弹向相反方向对步枪(炮弹)施加的力。b. 在无后坐力步枪中,炮弹不固定在步枪中;因此,当子弹被推向前移动时,炮弹被推开从枪管的另一端弹出。c. 站在无后坐力步枪后面是不安全的。
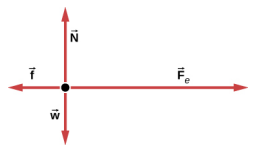
15。 a. 是的,力可以向左起作用;粒子会减速而失去速度。b. 是的,力可以向下起作用,因为即使向右移动,它的重量也会向下起作用。
17。 两种不同类型的力:向下的重量和向上作用的法向力
问题
19。 a.\(\vec{F}_{net}\) = 5.0\(\hat{i}\) + 10.0\(\hat{j}\) N
b. 幅度为 F net = 11 N,方向为\(\theta\) = 63°
21。 a.\(\vec{F}_{net}\) = 660.0\(\hat{i}\) + 150.0\(\hat{j}\) N
b. F net = 676.6 N at\(\theta\) = 距离大卫的绳子 12.8°
23。 a.\(\vec{F}_{net}\) = 95.0\(\hat{i}\) + 283\(\hat{j}\) N
b. 东北 71° 处 299 北
c.\(\vec{F}_{DS}\) = − (95.0\(\hat{i}\) + 283\(\hat{j}\)) N
25。 在静止状态下,短跑运动员在加速结束时达到 v = 12.96 m/s 的速度。 我们使用 x = 20.00 m = 0 + 0.5at 1 2 或 t 1 = 3.086 秒来计算加速时间。对于保持速度,x 2 = vt 2 或 t 2 = =\(\frac{x_{2}}{v}\)\(\frac{80.00\; m}{12.96\; m/s}\) = 6.173 秒。总时间 = 9.259 秒。
27。 a.m = 56.0 千克
b. a meas = a astro + 一艘飞船,其中一艘船 =\(\frac{m_{astro} a_{astro}}{m_{ship}}\)
c. 如果其他来源(宇宙飞船除外)可以对宇航员施加力,那么宇宙飞船就不会受到后坐力。
29。 F net = 4.12 x 10 5 N
31。 a = 253 m/s 2
33。 F net = F − f = ma\(\Rightarrow\) F = 1.26 x 10 3 N
35。 v 2 = v 0 2 + 2ax\(\Rightarrow\) a = −7.80 m/s 2,F net = −7.80 x 10 3 N
37。 a.\(\vec{F}_{net}\) = m\(\vec{a} \Rightarrow \vec{a}\) = 9.0\(\hat{i}\) m/s 2
b. 加速度的幅度为 9.0 m/s 2,所以 x = 110 m。
39。 1.6\(\hat{i}\) − 0.8\(\hat{j}\) m/s 2
41。 a.w M oon = mg M oon,m = 150 kg,w 地球 = 1.5 x 10 3 N
b. 质量没有变化,因此合适的宇航员在地球和月球上的质量均为150千克。
43。 a. F h = 3.68 x 10 3 N 和 w = 7.35 x 10 2 N,\(\frac{F_{h}}{w}\)= 比重量大 5.00 倍
b. F net = 3750 N,\(\theta\)= 距离水平线 11.3°
45。 w = 19.6 N,F net = 5.40 N,F net = ma\(\Rightarrow\) a = 2.70 m/s 2
47。 98 N
49。 497 N
51。 a. F 净值 = 2.64 x 10 7 N
b. 施加在船上的力也为 2.64 x 10 7 N,因为它与炮弹的运动方向相反。
53。 因为历史书的重量是地球对历史书施加的力,所以我们将其表示为\(\vec{F}_{EH}\) = −14\(\hat{j}\) N。除此之外,历史书只与物理书互动。 因为历史书的加速度为零,所以根据牛顿第二定律:,其上的净力为零\(\vec{F}_{PH} + \vec{F}_{EH} = \vec{0}\),物理书在历史书上施加的力在哪里\(\vec{F}_{PH}\)。 因此,\(\vec{F}_{PH} = − \vec{F}_{EH} = −(−14\; \hat{j})\; N = 14\; \hat{j}\; N\)。 我们发现物理学书籍在历史书上施加了 14 N 级的向上力。 物理书施加了三种\(\vec{F}_{EP}\)力量:来自地球、\(\vec{F}_{HP}\)历史书\(\vec{F}_{DP}\)和桌面。 由于物理学书重 18 N,\(\vec{F}_{EP} = −18\; \hat{j}\; N\). 从牛顿的第三定律来看\(\vec{F}_{HP} = − \vec{F}_{PH}\),所以\(\vec{F}_{HP} = −14\; \hat{j}\; N\)。 应用于物理学书籍的牛顿第二定律给出\(\Sigma \vec{F} = \vec{0}\)\(\vec{F}_{DP} + \vec{F}_{EP} + \vec{F}_{HP} = \vec{0}\),或者,所以\(\vec{F}_{DP}\) = − (−18\(\hat{j}\)) − (−14\(\hat{j}\)) = 32\(\hat{j}\) N。桌子在物理学书上施加了 32 N 的向上力。 为了得出这个解决方案,我们应用两次牛顿第二定律,一次应用牛顿第三定律。
55。 a. 最靠近脚部的滑轮的自由体图:
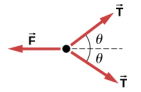
b. T = mg,F = 2T cos\(\theta\) = 2mg cos\(\theta\)
57。 a. 1.95 m/s 2
b. 1960 N
59。 a. T = 1.96 x 10 −4 N
b. T′ = 4.71 x 10 −4 N,\(\frac{T′}{T}\)= 垂直股张力的 2.40 倍
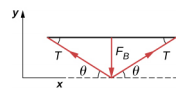
61。 \[\begin{split} F_{y\; net} = F_{\perp} - 2T \sin \theta & = 0 \\ F_{\perp} & = 2T \sin \theta \\ T & = \frac{F_{\perp}}{2 \sin \theta} \end{split}\]
63。 a. 参见示例 5.13
b. 1.5 N
c. 15 N
65。 a. 5.6 千克
b. 55 N
c. T 2 = 60 N
d。
67。 a. 4.9 m/s 2, 17 N
b. 9.8 N
69。
71。
其他问题
73。 5.90 千克
75。
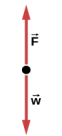
77。 a. F 净值 =\(\frac{m(v^{2} - v_{0}^{2})}{2x}\)
b. 2590 N
79。 \[\begin{split} \vec{F}_{net} & = 6.02\; \hat{i} + 14.0\; \hat{j}\; N \\ \vec{F}_{net} & = m \vec{a} \Rightarrow \vec{a} = 0.602\; \hat{i} + 1.40\; \hat{j}\; m/s^{2} \end{split}\]
81。 \[\begin{split} \vec{F}_{net} & = \vec{F}_{A} + \vec{F}_{B} \\ \vec{F}_{net} & = A \hat{i} + (-1.1A\; \hat{i} - 1.41A\; \hat{j}) \\ \vec{F}_{net} & = A(-0.41\; \hat{i} - 1.41\; \hat{j}) \end{split}\]
\(\theta\)= 254°(我们增加 180°,因为角度在象限 IV 中。)
83。 \(F = 2mk^{2}x^{2}\); 首先,取速度函数的导数来获得\(a = 2kxv = 2kx(kx^2) = 2k^{2}x^{3}\)。 然后应用牛顿第二定律\(F = ma = 2mk^{2}x^{2}\)。
85。 a. 对于方框 A,N A = mg,N B = mg cos\(\theta\)
b. N A > N B 因为对于\(\theta\) < 90°,cos\(\theta\) < 1
c. 当\(\theta\) = 10° 时 N A > N B
87。 a. 8.66 N
b. 0.433 m
89。 0.40 或 40%
91。 16 N
挑战问题
93。 一个。
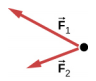
b. 否;\(\vec{F}_{R}\)未显示,因为它会取代\(\vec{F}_{1}\)和\(\vec{F}_{2}\)。 (如果我们想展示它,我们可以画出来,然后在上面放上\(\vec{F}_{1}\)波浪线,\(\vec{F}_{2}\)以表明它们不再被考虑。
95。 a. 14.1 m/s
b. 601 N
97。 \(\frac{F}{m}\)t 2
99。 936 N
101。 \(\vec{a}\)= −248\(\hat{i}\) − 433\(\hat{j}\) m/s 2
103。 0.548 m/s 2
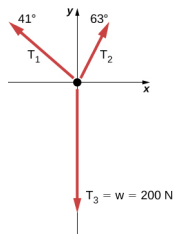
105。 a. T 1 =\(\frac{2mg}{\sin \theta}\)、T 2 =\(\frac{mg}{\sin (\arctan(\frac{1}{2} \tan \theta))}\)、T 3 =\(\frac{2mg}{\tan \theta}\)
b。\(\phi = \arctan(\frac{1}{2} \tan \theta)\)
c. 2.56°
d.x = d (2 cos\(\theta\) + 2 cos (arct\(\frac{1}{2}\) an (tan\(\theta\))) + 1)
107。 a.\(\vec{a}\) = (5.00 m\(\hat{i}\) + 3.00 m\(\hat{j}\)) m/s 2
b. 1.38 千克
c. 21.2 m/s
d.\(\vec{v}\) = (18.1\(\hat{i}\) + 10.9\(\hat{j}\)) m/s 2
109。 a. 0.900\(\hat{i}\) + 0.600\(\hat{j}\) N
b. 1.08 N


