18.4：二维和三维运动

Last updated
Save as PDF

Page ID: 204485

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

检查你的理解

4.1。 (a) 取相对于位置函数时间的导数，我们有$\vec{v}$ (t) = 9.0t ²$\hat{i}$ 且$\vec{v}$ (3.0s) = 81.0$\hat{i}$ m/s。(b) 由于速度函数是非线性的，我们怀疑平均速度不等于瞬时速度。我们检查了这个然后发现 $$\ vec {v} _ {avg} =\ frac {\ vec {r} (t_ {2})-\ vec {r} (t_ {1})} {t_ {2}-t_ {1}} =\ frac {\ vec {r} (4.0\; s)-\ vec {r} (2.0\; s) {4.0\; s-2.0\; s} =\ frac {(188.0\;\ hat {i}-20.0\;\ hat {i})\; m} {2.0\; s} = 84.0\;\ hat {i}\; m/s，$$ 不同于$\vec{v}$ (3.0$\hat{i}$ 秒) = 81.0 m/s。

4.2。 加速度向量是恒定的，不会随时间而变化。如果 a、b 和 c 不为零，则速度函数在时间上必须是线性的。我们有$\vec{v}$ (t) =$\int \vec{a}$ dt =$\int$ (a$\hat{i}$ + b$\hat{j}$ + c$\hat{k}$) dt = (a$\hat{i}$ + b$\hat{j}$ + c$\hat{k}$) t m/s，因为取速度函数的导数会产生$\vec{a}$ (t)。如果加速度的任何分量为零，则速度的该分量将是一个常数。

4.3。 (a) 选择从坐标系原点抛出岩石的悬崖顶部。尽管它是任意的，但我们通常选择时间 t = 0 来对应原点。 (b) 描述水平运动的方程为 x = x ₀ + v x t。当 _x _{0 = 0} 时，该方程变成 x = v _x t。(c) 方程 4.27 到方程 4.29，方程 4.46 描述垂直运动，但由于 y ₀ = 0 和 v _0y =0，这些方程大大简化为 y =$\frac{1}{2}$ (v _0y + v _y) t =$\frac{1}{2}$ v _y t、v _y = −gt、y = −$\frac{1}{2}$ gt ² 和 v _y ² = −2gy。 (d) 我们使用运动学方程来找出撞击点速度的 x 和 y 分量。使用 v _y ² = −2gy 并注意撞击点为 −100.0 m，我们发现撞击速度的 y 分量为 v _y = 44.3 m/s。我们得到 x 分量，v _x = 15.0 m/s，因此我们可以计算出撞击时的总速度：v = 46.8 m/s$\theta$= 水平线以下 71.3°。

4.4。 高尔夫球以 30° 射门。

4.5。 134.0 cm/s

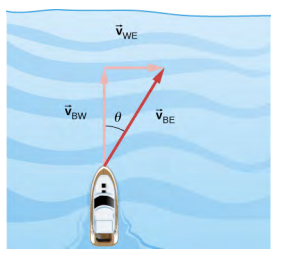
4.6。 标注矢量方程的下标，我们有 B = 船，R = 河流，E = 地球。向量方程变为$\vec{v}_{BE}$ =$\vec{v}_{BR}$ +$\vec{v}_{RE}$。我们的直角三角形几何如下图所示。求解$\vec{v}_{BE}$，我们有 $$v_ {BE} =\ sqrt {v_ {BR} ^ {2} + v_ {RE} ^ {2}} =\ sqrt {4.5^ {2} + 3.0^ {2}} $$$$v_ {BE} = 5.4\; m/s，\ quad\ theta =\ tan^ {-1}\ 左 (\ dfrac {4.5}}\ right) = 33.7^ {o}\ ldotp\]

向量 V sub W、V sub W E 和 V sub B E 形成直角三角形。在 V sub B W 和 V sub B E 的尾巴交汇处显示了一条船。向量 V sub B W 指向上方。 V sub W E 指向右边。 V sub B E 指向上和向右，与垂直方向成一定角度。 V sub B E 是 v sub B W 和 V sub W E 的矢量和

概念性问题

1。直线

3。斜率必须为零，因为速度矢量与位置函数的图形相切。

5。不，垂直方向上的运动是独立的。

7。 a. 否；b. 弹道顶点的最小值和发射和撞击时的最大值；c. 不，速度是一个矢量；d. 是的，它降落在哪里

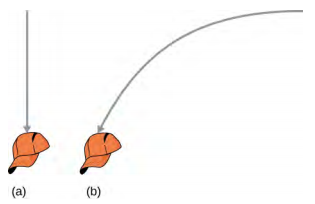
9。他们俩同时撞到了地面。

11。 是的

13。如果他要将球传给另一名球员，他需要密切关注队伍中其他球员所在的参考框架。

15。

图 a：一顶帽子的轨迹是直线向下的。图 b：帽子的轨迹是抛物线，向下向左弯曲。

问题

17。 $\vec{r}$= 1.0$\hat{i}$ − 4.0$\hat{j}$ + 6.0$\hat{k}$

19。 $\Delta \vec{r}_{Total}$= 472.0 m$\hat{i}$ + 80.3 m$\hat{j}$

21。 位移总和 = −6.4 km$\hat{i}$ + 9.4 km$\hat{j}$

23。 a.$\vec{v}$ (t) = 8.0t$\hat{i}$ + 6.0t ²$\hat{k}$，$\vec{v}$(0) = 0，$\vec{v}$(1.0) = 8.0$\hat{i}$ + 6.0$\hat{k}$ m/s

b.$\vec{v}_{avg}$ = 4.0$\hat{i}$ + 2.0$\hat{k}$ m/s

25。 $\Delta \vec{r}_{1}$= 20.00 m$\hat{j}$，$\Delta \vec{r}_{2}$=（2.000 x 10 ⁴ m）（cos 30°$\hat{i}$ + sin 30°$\hat{j}$），$\Delta \vec{r}$= 1.700 x 10 ⁴ m$\hat{i}$ + 1.002 x 10 ⁴ m$\hat{j}$

27。 a.$\vec{v}$ (t) = (4.0t$\hat{i}$ + 3.0t$\hat{j}$) m/s，$\vec{r}$(t) = (2.0t ²$\hat{i}$ +$\frac{3}{2}$ t ²$\hat{j}$) m

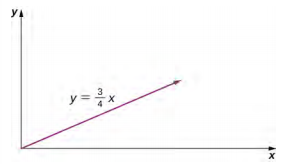
b.x (t) = 2.0t 2m，y (t) =$\frac{3}{2}$ t ² m，t ² =$\frac{x}{2} \Rightarrow$ y =$\frac{3}{4}$ x

线性函数 y 的图形等于 3 个季度 x。该图是一条穿过原点的正斜率直线。

29。 a.$\vec{v}$ (t) = (6.0t$\hat{i}$ − 21.0t ²$\hat{j}$ + 10.0t ⁻³$\hat{k}$) m/s

b.$\vec{a}$ (t) = (6.0$\hat{i}$ − 42.0t$\hat{j}$ − 30t ⁻⁴$\hat{k}$) m/s ²

c.$\vec{v}$ (2.0s) = (12.0$\hat{i}$ − 84.0$\hat{j}$ + 1.25$\hat{k}$) m/s

d.$\vec{v}$ (1.0 s) = (6.0$\hat{i}$ − 21.0$\hat{j}$ + 10.0$\hat{k}$) m/s，|$\vec{v}$ (1.0 s) | = 24.0 m/s；$\vec{v}$(3.0 s) = (18.0$\hat{i}$ − 189.0$\hat{j}$ + 0.37$\hat{k}$) m/s，|$\vec{v}$ (3.0 秒) | = 190.0 m/s

e.$\vec{r}$ (t) = (3.0t ²$\hat{i}$ − 7.0t ³$\hat{j}$ − 5.0t ⁻²$\hat{k}$) cm，$\vec{v}_{avg}$= (9.0$\hat{i}$ − 49.0$\hat{j}$ − 6.3$\hat{k}$) m/s

31。 a.$\vec{v}$ (t) = −sin (1.0t)$\hat{i}$ + cos (1.0t)$\hat{j}$ +$\hat{k}$

b.$\vec{a}$ (t) = −cos (1.0t)$\hat{i}$ − sin (1.0t)$\hat{j}$

33。 a.t = 0.55 秒

b.x = 110 m

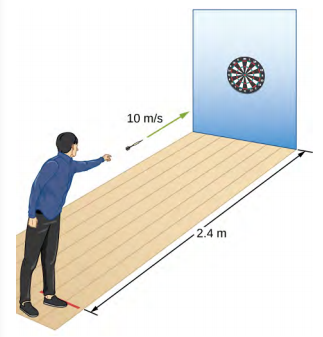
35。 a.t = 0.24s，d = 0.28 m

b. 他们的目标很高。

一个人投掷飞镖的插图。飞镖在距离飞镖板 2.4 米处水平释放，与飞镖板的牛眼保持水平，速度为每秒 10 米。

37。 a.t = 12.8 秒，x = 5619 m

b.v _y = 125.0 m/s，v _x = 439.0 m/s，$\vec{v}$| = 456.0 m/s

39。 a.v _y = v _0y − gt，t = 10s，v _y = 0，v _0y = 98.0 m/s，v _{0 = 196.0} m/s

b.h = 490.0 m

c.v _0x = 169.7 m/s，x = 3394.0 m

d.x = 2545.5 m，y = 367.5 m，$\vec{s}$= 2545.5 m$\hat{i}$ + 367.5 m$\hat{j}$

41。 −100 m = (−2.0 m/s) t − (4.9 m/s ²) t ²、t = 4.3 秒、x = 86.0 m

43。 R _Moon = 48 m

45。 a.v _0y = 24 m/s，v _y ² = v _0y ² − 2gy$\Rightarrow$ h = 23.4 m

b.t = 3 秒，v _0x = 18 m/s，x = 54 m

c.y = −100 m，y ₀ = 0，y − y ₀ = v _0y，t −$\frac{1}{2}$ gt ² − 100 = 24t − 4.9t ²$\Rightarrow$ t = 7.58 s

d.x = 136.44 m

e.$$\ begin {split} t & = 2.0\; s，y = 28.4\; m，x = 36\; m\\ t & = 4.0\; s，y = 17.6\; m\\ t & = 6.0\; s，y = −32.4\; m，x = 108\; m\ end {split}\]

47。 v _0y = 12.9 m/s，y − y ₀ = v _0y t −$\frac{1}{2}$ gt ² − 20.0 = 12.9t − 4.9t ²

t = 3.7 秒，v _0x = 15.3 m/s$\Rightarrow$ x = 56.7 m

因此，高尔夫球手的射门落在距离果岭13.3米的地方。

49。 a. R = 60.8 m

b. R = 137.8 m

51。 a.v _y ² = v _0y ² − 2g$\Rightarrow$ y y = 2.9 m/s

y = 3.3 m/s

y =$\frac{v_{0y}^{2}}{2g}$$\frac{(v_{0} \sin \theta)^{2}}{2g} \Rightarrow \sin \theta$ = 0.91$\Rightarrow$$\theta$ = 65.5°

53。 R = 18.5 m

55。 y = (tan$\theta_{0}$) x −$\Big[ \frac{g}{2(v_{0} \cos \theta_{0})^{2}} \Big]$ x ²$\Rightarrow$ v ₀ = 16.4 m/s

57。 R$\frac{v_{0}^{2} \sin 2 \theta_{0}}{g} \Rightarrow \theta_{0}$ = 15.0°

59。 宽接球手需要 1.1 秒才能覆盖他跑步的最后 10 米。

T _tof$\frac{2(v_{0} \sin \theta)}{g} \Rightarrow \sin \theta$ = 0.27$\Rightarrow \theta$ = 15.6°

61。 a _C = 40 m/s ²

63。 a _C =$\frac{v^{2}}{r} \Rightarrow$ v ² = r，a _C = 78.4，v = 8.85 m/s

T = 5.68 秒，即 0.176 rev/s = 10.6 rev/min

65。 金星距离太阳 1.082 亿公里，轨道周期为 0.6152 y。

r = 1.082 x 10 ¹¹ m，T = 1.94 x 10 ⁷ 秒

v = 3.5 x 10 ⁴ m/s，a _C = 1.135 x 10 ^{−2 m} /s ²

67。 360 转/分钟 = 6 转/秒

v = 3.8 m/s，a _C = 144。m/s ²

69。 a. O′ (t) = (4.0$\hat{i}$ + 3.0$\hat{j}$ + 5.0$\hat{k}$) t m

b.$\vec{r}_{PS}$ =$\vec{r}_{PS'}$ +$\vec{r}_{S'S}$，$\vec{r}$(t) =$\vec{r′}$ (t) + (4.0$\hat{i}$ + 3.0$\hat{j}$ + 5.0$\hat{k}$) t m

c.$\vec{v}$ (t) =$\vec{v′}$ (t) + (4.0 + 3.0$\hat{i}$$\hat{j}$ + 5.0$\hat{k}$) m/s

d. 加速度相同。

71。 $\vec{v}_{PC}$= (2.0$\hat{i}$ + 5.0$\hat{j}$ + 4.0$\hat{k}$) m/s

73。 a. A = 空气，S = 海鸥，G = 地面

$\vec{v}_{SA}$= 9.0 m/s，海鸥相对于静止空气的速度

$\vec{v}_{AG}$=？，$\vec{v}_{SG}$= 5 m/s，$\vec{v}_{SG} = \vec{v}_{SA} + \vec{v}_{AG} \Rightarrow \vec{v}_{AG} = \vec{v}_{SG} − \vec{v}_{SA}$

$\vec{v}_{AG}$= −4.0 m/s

b.$\vec{v}_{SG} = \vec{v}_{SA} + \vec{v}_{AG} \Rightarrow \vec{v}_{SG}$ = −13.0 m/s

$\frac{−6000\; m}{−13.0\; m/s}$= 7 分 42 秒

75。 以正方向为与河流流向的方向相同，即向东。 S = 海岸/地球，W = 水，B = 船。

a.$\vec{v}_{BS}$ = 11 km/h，t = 8.2 分钟

b.$\vec{v}_{BS}$ = −5 km/h，t = 18 分钟

c.$\vec{v}_{BS} = \vec{v}_{BW} + \vec{v}_{WS}, \theta$ = 北向西 22°

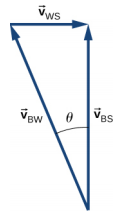
向量 V sub W、V sub W S 和 V sub B S 形成直角三角形，V sub B W 作为斜边。 V sub B S 点向上。 V sub W S 指向右边。 V sub B W 向上和向左指向，与垂直方向成一角 theta。 V sub B S 是 v sub B W 和 V sub W S 的矢量和

d.$\vec{v}_{BS}$ | = 7.4 km/h，t = 6.5 分钟

e.$\vec{v}_{BS}$ = 8.54 km/h，但只使用直过河流的速度分量来获取时间

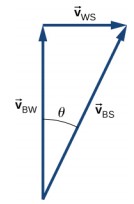
向量 V sub W、V sub W S 和 V sub B S 形成直角三角形，V sub B S 作为斜边。 V sub B W 指向上方。 V sub W S 指向右边。 V sub B S 向上和向右指向，与垂直方向成一角 theta。 V sub B S 是 v sub B W 和 V sub W S 的矢量和

t = 6.0 分钟

下游 = 0.3 千米

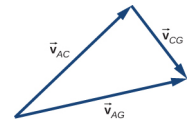
77。 $\vec{v}_{AG} = \vec{v}_{AC} + \vec{v}_{CG}$

|$\vec{v}_{AC}$ | = 25 km/h，$\vec{v}_{CG}$| = 15 km/h，$\vec{v}_{AG}$| = 29.15 km/h，$\vec{v}_{AG} = \vec{v}_{AC} + \vec{v}_{CG}$

$\vec{v}_{AC}$和之间的角度$\vec{v}_{AG}$为 31°，因此风向为东向北 14°。

向量 V sub A C、V sub C G 和 V sub A G 形成三角形。 V sub A C 和 V sub C G 成直角。 V sub A G 是 v sub A C 和 V sub C G 的矢量和

其他问题

79。 a _C = 39.6 m/s ²

81。 90.0 km/h = 25.0 m/s，9.0 km/h = 2.5 m/s，60.0 km/h = 16.7 m/s

a _T = −2.5 m/s ²，a _C = 1.86 m/s ²，a = 3.1 m/s ²

83。 纬度处的旋转圆的半径$\lambda$为 R _E cos$\lambda$。身体的速度为$\frac{2 \pi r}{T}$。a _{C = f}$\frac{4 \pi^{2} R_{E} \cos \lambda}{T^{2}}$ or$\lambda$ = 40°，a _C = 0.26% g

85。 a _T = 3.00 m/s ²

v (5 s) = 15.00 m/s，a _C = 150.00 m/s ²，$\theta$= 88.8° 相对于向内的旋转圆的切线。

|$\vec{a}$ | = 150.03 m/s ²

87。 $\vec{a}$(t) = −A$\omega^{2}$ cos$\omega$ t$\hat{i}$ − A$\omega^{2}$ sin$\omega$ t$\hat{j}$

a _C = 5.0 m$\omega^{2}$，$\omega$= 0.89 rad/s

$\vec{v}$(t) = −2.24 m/s$\hat{i}$ − 3.87 m/s$\hat{j}$

89。 $\vec{r}_{1}$= 1.5$\hat{j}$ + 4.0$\hat{k}$，$\vec{r}_{2} = \Delta \vec{r} + \vec{r}_{1}$= 2.5$\hat{i}$ + 4.7$\hat{j}$ + 2.8$\hat{k}$

91。 v _x (t) = 265.0 m/s，v _y (t) = 20.0 m/s，$\vec{v}$(5.0 s) = (265.0$\hat{i}$ + 20.0$\hat{j}$) m/s

93。 R = 1.07 m

95。 v ₀ = 20.1 m/s

97。 v = 3072.5 m/s，a _C = 0.223 m/s ²

挑战问题

99。 a. −400.0 m = v _0y t − 4.9t ²，359.0 m = v _0x t，t =$\frac{359.0}{v_{0x}}$ − 400.0 = 359.0$\frac{v_{0y}}{v_{0x}}$ − 4.9$\left(\dfrac{359.0}{v_{0x}}\right)^{2}$

−400.0 = 359.0 tan 40 −$\frac{631,516.9}{v_{0x}^{2}} \Rightarrow$ v _0x ² = 900.6，v _0x = 30.0 m/s，v _{0y = v 0} _x tan 40 = 25.2 m/s，v = 39.2 m/s

b.t = 12.0 秒

101。 a.$\vec{r}_{TC}$ = (−32 + 80t)$\hat{i}$ + 50t$\hat{j}$，$\vec{r}_{TC}$| ² = (−32 + 80t) ² + (50t) ²

2r$\frac{dr}{dt}$ = 2 (−32 + 80t) + 100t，$\frac{dr}{dt} = \frac{2(−32 + 80t) + 100t}{2r}$= 0

260t = 64$\Rightarrow$ t = 15 分钟

b. |$\vec{r}_{TC}$ | = 17 km