18.3: 沿直线运动

Last updated
Save as PDF

Page ID: 204559

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

检查你的理解

3.1。 (a) 骑手的排水量为$\Delta$ x = x _f − x ₀ = −1 km。（位移量为负，因为我们将东部视为正数，西部为负数。） (b) 行进距离为 3 千米+ 2 千米 = 5 千米。 (c) 位移幅度为1千米。

3.2。 (a) 取x (t) 的导数得出 v (t) = −6t m/s。(b) 不，因为时间永远不可能为负。 (c) 速度为 v (1.0 s) = −6 m/s，速度为 |v (1.0 s) | = 6 m/s。

3.3。 插入已知数，我们有$\bar{a} = \frac{\Delta v}{\Delta t} = \frac{2.0 \times 10^{7}\; m/s − 0}{10^{−4}\; s − 0} = 2.0 \times 10^{11}\; m/s^{2}$。

3.4。 如果我们以东为正，则飞机加速度为负，因为它正在向西加速。它也在减速；它的加速度与其速度的方向相反。

3.5。 要回答这个问题，请选择一个允许我们求解时间 t 的方程，假设只有 a、v _{0 和} v$$v = v_ {0} + at\ ldotp$$ 重新排列求解 t: $$t =\ frac {v − v_ {0}} {a} =\ frac {400\; m/s − 0\; m/s} {20\; m/s {2}} = 20 s\ ldotp\]

3.6。 a =$\frac{2}{3}$ m/s ²。

3.7。 落水需要 2.47 秒。行进距离的增加速度更快。

3.8。 a. 速度函数是加速度函数的积分加上积分常数。 _{根据方程 3.91，$$v (t) =\ int a (t) dt + C_ {1} =\ int (5 − 10t) dt + C_ {1} = 5t − 5t^ {2} + C_ {1}\ ldotp$$ 由于 v (0) = 0，所以，$$v (t) = 5t − 5t^ {2}\ ldotp$$ b。根据方程 3.93，$$x (t) =\ int v (t) dt + C_ {2} =\ int (5t − 5t^ {2}) dt + C_ {2} =\ frac {5} {3} t^ {3} + C_ {2}}ldotp$$ 由于 x (0) = 0，我们有 C ₂ = 0，$$x (t) =\ frac {5} {2} t^ {2} −\ frac {5} {3} t^ {3}\ ldotp$$ c。速度可以写成 v (t) = 5t (1 — t)，t = 0 时等于零，t = 1 s。

概念性问题

1。你开车进入城里，然后回来开车经过你的房子去朋友家。

3。如果细菌来回移动，那么位移就会相互抵消，最终的移位很小。

5。行进距离

7。平均速度等于总行驶距离除以经过的时间。如果你去散步，离开然后回到家，你的平均速度是正数。由于平均速度 = 位移/经过时间，因此您的平均速度为零。

9。平均速度。如果汽车不反转方向，它们是一样的。

11。 不，在一维空间中，恒定速度需要零加速度。

13。 球被抛向空中，其速度在投掷顶点为零，但加速度不为零。

15。 加上，减去

17。 如果加速度、时间和位移是已知数，而初始速度和最终速度是未知数，则必须同时求解两个运动学方程。此外，如果最终速度、时间和位移已知，则必须求解初始速度和加速度的两个运动学方程。

19。 a. 在轨迹的顶端；b. 是的，在轨迹的顶端；c. 是的

21。 earth$$V = v_ {0} − gt = −gt; $$ moon$v′ =\ frac {g} {6} t'$$$ $v = v′ − gt = −\ frac {g} {6} t′ $$t = 6t；$$ Earth $$y = −\ frac {1} {2} gt^ {2} $$$ y′ = −\ frac {1} {2}\ frac {g} {6} (6t) ^ {2} = −\ frac {1} {2} g6t^ {2} = −6\ 左 (\ dfrac {1} {2} gt^ {2}\ 右) = −6y\]

问题

25。 a.$\vec{x}_{1}$ = (−2.0 m)$\hat{i}$,$\vec{x}_{2}$ = (5.0 m)$\hat{i}$

b. 向东 7.0 米

27。 a.t = 2.0 秒

b.x (6.0) − x (3.0) = −8.0 − (−2.0) = −6.0 m

29。 a. 150.0 秒，$\vec{v}$= 156.7 m/s

b. 海平面声速的 45.7%

31。

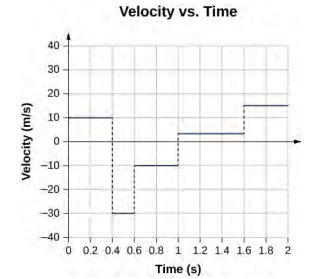
图表显示了以米/秒为单位绘制的速度，以秒为单位绘制的时间函数。速度以每秒 10 米开始，0.4 秒时减小到 -30；0.6 秒时增加到 -10 米，1 秒时增加到 5 米，1.6 秒时增加到 15。

33。

图表显示了绘制的位置与时间的关系。它从原点开始，增加到最大值，然后减小到接近零。

35。 a.v (t) = (10 − 4t) m/s；v (2 s) = 2 m/s，v (3 s) = −2 m/s

b. |v (2 s) | = 2 m/s，|v (3 s) | = 2 m/s

c.$\bar{v}$ = 0 m/s

37。 a = 4.29 m/s ²

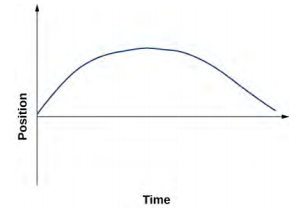
39。

图表显示了以米/秒为单位的加速度与时间（以秒为单位）的平方。加速度为每秒 0.3 米，介于 0 到 20 秒之间，每秒 -0.1 米平方，20 到 50 秒之间，0 到 70 秒之间为零，90 到 100 秒之间为 -0.6。

41。 a = 11.1g

43。 150 m

45。 上午 525 米

b.v = 180 m/s

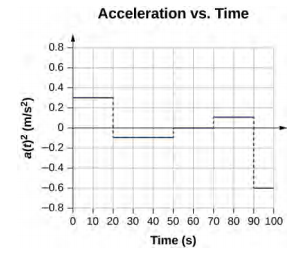
47。 一个。

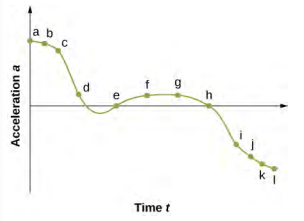
图形是加速度 a 作为时间 t 函数的图。图形是非线性的，加速度在起点为正，终点为负，在点 d 和 e 之间以及点 e 和 h 处交叉 x 轴。

b. 加速度在 t _a c 处的正值最大。t _e 和 t _h d 处的加速度为零。t _i、t _j、t _k、t _l 处的加速度为负

49。 a.a = −1.3 m/s ²

b.v ₀ = 18 m/s

c.t = 13.8 秒

51。 v = 502.20 m/s

53。 一个。

该图显示了速度等于 0 米每秒、加速度等于 2.4 米每秒的物体，零点处的平方。当时间等于 12 秒时，加速度保持等于每秒 2.4 米。物体的速度和位置未知。

^{b. 已知数：a = 2.40 m/s ²，t = 12.0 s，v ₀ = 0 m/s，x ₀ = 0 m；c.x = x ₀ _{+ v 0}$\frac{1}{2}$ t + a$\frac{1}{2}$ t ² = 2.40 m/s ² (12.0 s) ² = 172.80 m，答案似乎合理}172.8 m；d.v = 28.8 m/s

55。 一个。

该图显示了起始速度为零且加速度未知的物体。在未知时间之后，物体达到每秒 30 厘米的速度，距离起点 1.8 厘米。此时物体的加速度尚不清楚。

b. 已知数：v = 30.0 cm/s，x = 1.80 cm

c.a = 250 cm/s ²，t = 0.12 秒

d. 是的

57。 a. 6.87 m/s ²

b.x = 52.26 m

59。 a.a = 8450 m/s ²

b.t = 0.0077 秒

61。 a.a = 9.18g

b.t = 6.67 x 10 ⁻³ s

c.a = −40.0 m/s ²，a = 4.08g

63。 已知：x = 3 m，v = 0 m/s，v0 = 54 m/s。我们想要 a，所以我们可以使用这个方程：a = −486 m/s ²。

65。 a.a = 32.58 m/s ²

b.v = 161.85 m/s

c.v > v _max，因为恒定加速度的假设对赛车无效。高速赛车换档，第一档的加速度比第二档的加速度大于第三档的加速度，依此类推。一开始加速度最大，因此在最后几米内它不会以32.6 m/s ² 的速度加速，而是要低得多，最终速度将小于162 m/s。

67。 a.y = −8.23 m，v ₁ = −18.9 m/s

b.y = −18.9 m，v ₂ = 23.8 m/s

c.y = −32.0 m，v ₃ = −28.7 m/s

d. y = −47.6 m，v ₄ = −33.6 m/s

e.y = −65.6 m，v ₅ = −38.5 m/s

69。 a. 已知数：a = −9.8 m/s ²，v ₀ = −1.4 m/s，t = 1.8 秒，y ₀ = 0 m

b.y = y ₀ + v ₀ t −$\frac{1}{2}$ gt ²，y = v ₀ t −$\frac{1}{2}$ gt = −1.4 m/s（1.8 秒）−$\frac{1}{2}$（9.8）（1.8 s）² = −18.4 m 起点在距离水面 18.4 米的救援人员身上。

71。 a.v ² = v ₀ ² − 2g (y − y ₀)、y ₀ = 0、v = 0、y =$\frac{v_{0}^{2}}{2g}$$\frac{(4.0 m/s)^{2}}{2(9.80)}$ = 0.82 m

b. 到顶点 v = 0.41 秒乘以 2 到棋盘 = 0.82 秒从棋盘到水面 y = y ₀ _{+ v 0}$\frac{1}{2}$ t − gt ²，y = −1.8 ₀ m，y 0 = 4. ₀ m/s −1.8 = 4.0t − 4.9t ²，4.9t 2 − 4.0t − 1.80 = 0，二次方程解给出 1.13 秒

c.v ² = v ₀ ² − 2g (y − y _{0) y 0} = ₀，v 0 = 4. ₀ m/s，y = −1.80 m，v = 7.16 m/s

73。 到达顶点的时间：t = 1.12 秒乘以 2 等于 2.24 秒到高度 2.20 m。到 1.80 米的高度是额外的 0.40 m.$$y = y_ {0} + v_ {0} t −\ frac {1} {2} $$$y = −0.40\; m$$$$y_ {0} = 0$$v_ {0} = −11.0\; m/s$$$$−0.40 = −11.0t − 4.9t^ {2}\; 或\; 4.9t^ {2} + 11.0t − 0.40 = 0\ ldotp$$ 取正根，所以再走 0.4 m 的时间为 0.04 秒。总时间为 2.24 秒 + 0.04 秒 = 2.28 秒。

75。 a.v ² = v ₀ ² − 2g (y − y ₀)、y _{0 = 0}、v = 0、y = 2.50 m、$$v_ {0} ^ {2} = 2gy\ Rightarrow v_ {0} =\ sqrt {2 (9.80) (2.50)} = 7.0\; m/s;\]

b.t = 0.72 秒乘以 2 给出空中 1.44 秒

77。 a.v = 70.0 m/s

b. 岩石开始掉落后听到的时间：0.75 秒，到达地面的时间：6.09 秒

79。 a. A = m/s ²，B = m/s ^5/2

b.v (t) =$\int$ a (t) dt + C ₁ =$\int$ (A − Bt ^1/2) dt + C ₁ = At −$\frac{2}{3}$ Bt ^3/2 + C ₁\[v(0) = 0 = C_{1}\; so\; v(t_{0}) = At_{0} − \frac{2}{3} Bt_{0}^{3/2};\]

c.x (t) =$\int$ v (t) dt + C ₂ =$\int$ (At −\ frac {2} {3}\) Bt ³ ^/2) dt + C ₂ = A$\frac{1}{2}$ t ² −$\frac{4}{15}$ Bt ^5/2 + C ₂\[x(0) = 0 = C_{2}\; so\; x(t_{0}) = \frac{1}{2} At_{0}^{2} − \frac{4}{15} Bt_{0}^{5/2}\]

81。 a. $$\ begin {split} a (t) & = 3.2 m/s^ {2}\ quad t\ leq 5.0\; s\\ a (t) & = 1.5\; m/s^ {2}\ quad 5.0\; s\ leq t\ leq 11.0\; s\ end {split}\]

b. $$\ begin {split} x (t) & =\ int v (t) dt + C_ {2} =\ int 3.2tdt + C_ {2} = 1.6t^ {2} + C_ {2}\ quad t\ leq 5.0\; s\\ x (0) & = 0\; 因此，\; x (2.0\; s) = 6.4\; m\\ x (t) & =\ int v (t) dt + C_ {2} =\ int [16.0 − 1.5 (t − 5.0)] dt + C_ {2} = 16t − 1.5\ 左 (\ dfrac {t^ {2}} {2} − 5.0t\ 右)+ C_ {2}\ quad 5.0\; s\ leq t\ leq 11.0\; s\\ x (5\; s) & = 1.6 (5.0) ^ {2} = 40\; m = 16 (5.0\; s) − 1.5\ 左 (\ dfrac {5^ {2}} {2} − 5.0 (5.0)\ 右) + C_ {2}\ end {split} $$$\ begin {split} 40 & = 98.75 + C_ {2}\ Rightarrow C_ {2} = −58.75\\ x (7.0 s) & = 16 (7.0) − 1.5\ 左 (\ dfrac {7^ {2}} {2} − 5.0 (7)\ 右) − 58。75 = 69\; m\\ x (t) & =\ int 7.0dt + C_ {2} = 7t + C_ {2}\ quad t\ geq 11.0\; s\\ x (11.0\; s) & = 16 (11) − 1.5\ 左 (\ dfrac {11^ {2}} {2} − 5.0 (11)\ 右) − 58.75 = 7 (11.0\; s) + C_ {2}\ Rightarrow C_ {2} = 32\; m\\ x (t) & = 7t + 32\; m\ quad x\ geq 11.0\; s\ Rightarrow x (12.0\; s) = 7 (12) + 32 =116\; m\ end {split}\]

其他问题

83。 向西行驶为正方向。第一架飞机：$\bar{v}$= 600 km/h；第二架飞机：$\bar{v}$= 667.0 km/h

85。 a =$\frac{v − v_{0}}{t − t_{0}}$，t = 0，a$\frac{−3.4\; cm/s − v_{0}}{4\; s}$ = 1.2 cm/s ²$\Rightarrow$ v ₀ = − 8.2 cm/s，v = v ₀ + at = − 8.2 + 1.2 t；v = −7.0 cm/s，v = −1.0 cm/s

87。 a = −3 m/s ²

89。 a.v = 8.7 x 10 ⁵ m/s

b.t = 7.8 x 10 ⁻⁸ 秒

91。 1 km = v ₀ (80.0 s) +$\frac{1}{2}$ a (80.0) ²；2 km = v ₀ (200.0) +$\frac{1}{2}$ a (200.0) ² 同时求解得到 a = km$− \frac{0.1}{2400.0}$ /s ² 和 v ₀ = 0.014167 km/s，即 51.0 km/h。行程结束时的速度为 v = 21.0 km/h。

93。 a = −0.9 m/s ²

95。 超速驾驶汽车的方程式：这辆车的速度恒定，即平均速度，并且没有加速，所以使用位移方程式 x ₀ = 0: x = x ₀ +$\bar{v}$ t =$\bar{v}$ t；警车方程：这辆车正在加速，所以使用_{x _{0 = 0 和 v 0} = 0 的位移方程，因为警车从静止处开始：x = x _{0 + v ₀} t + a$\frac{1}{2}$ t ² = a$\frac{1}{2}$ t ^{2 = at 2}；现在我们有了一个具有共同参数的每辆车的运动方程，可以是}被淘汰以找到解决方案。在这种情况下，我们求解 t。步骤 1，消除 x: x =$\bar{v}$ t =$\frac{1}{2}$ at ²；步骤 2，求解 t: t =$\frac{2 \bar{v}}{a}$。超速驾驶汽车的恒定速度为40 m/s，这是其平均速度。警车的加速度为 4 m/s ²。评估 t，即警车到达超速驾驶汽车的时间，我们得出 t$\frac{2 \bar{v}}{a}$ =$\frac{2(40)}{4}$ = 20 秒。

97。 在这次加速下，她在 t =$\frac{−v_{0}}{a}$$\frac{8}{0.5}$ = 16 秒内进入句号，但覆盖的距离为 x = 8 m/s (16 s) −$\frac{1}{2}$ (0.5) (16 s) ² = 64 m，这小于她距离终点线的距离，因此她从未完成比赛。

99。 x ₁ =$\frac{3}{2}$ v ₀ t；x ₂ =$\frac{5}{3}$ x ₁

101。 v ₀ = 窗口底部的速度 7.9 m/s。v = 7.9 m/s；v ₀ = 14.1 m/s

103。 a.v = 5.42 m/s

b.v = 4.64 m/s

c.a = 2874.28 m/s ²

d. (x − x ₀) = 5.11 x 10 ⁻³ m

105。 假设玩家在 1.0 m 和 0.3 m 的高度从静止状态中掉下来。0.9 秒；0.5 秒

107。 a.t = 6.37 秒取正根

b.v = 59.5 m/s

109。 a.y = 4.9 m

b.v = 38.3 m/s；c. −33.3 m

111。 h =$\frac{1}{2}$ gt ²，h = 总高度和掉落地面的时间$\frac{2}{3}$ h =$\frac{1}{2}$ g (t − 1) ² in t — 1 秒钟它会掉落$\frac{2}{3}$ h$$\ frac {2} {3}\ 左 (\ dfrac {1} {2}\ 右) =\ frac {1} {2} g ^ {2}\; 或\;\ frac {t^ {2}} {3} =\ frac {1} {2} (t − 1) ^ {2} $$$0 = t^ {2} − 6t +3,\; t =\ frac {6\ pm\ sqrt {62 − 4\ cdotp 3}} {2} = 3\ pm\ frac {\ sqrt {24}} {2} $$ t = 5.45 s 和 h = 145.5 m。其他根小于 1 秒。检查 t = 4.45 秒，h =$\frac{1}{2}$ gt ² = 97.0 m =$\frac{2}{3}$ (145.5)

挑战问题

113。 a.v (t) = 10t − 12t ² m/s，a (t) = 10 − 24t m/s ²

b.v (2 s) = −28 m/s，a (2 s) = −38m/s ²

c. 位置函数的斜率为零或速度为零。有两种可能的解：t = 0，它给出 x = 0，或 t$\frac{10.0}{12.0}$ = 0.83 s，得出 x = 1.16 m。第二个答案是正确的选择

d. 0.83 秒

e. 1.16 m

115。 96 km/h = 26.67 m/s，a$\frac{26.67\; m/s}{4.0\; s}$ = 6.67m/s ²，295.38 km/h = 82.05 m/s，t = 12.3 秒加速到最大速度；x = 504.55 m = 加速期间覆盖的距离；恒定速度为 7495.44 米；$\frac{7495.44\; m}{82.05\; m/s}$= 91.35 秒所以总时间为 91.35 秒 + 12.3 秒 = 103.65 秒。