Skip to main content
Global

17.E：声音（练习）

  1. Last updated
  2. Save as PDF
  • Page ID
    204232

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    概念性问题

    17.1 声波

    1. 声音和听觉有什么区别？
    2. 您将了解到光是一种可以在真空中传播的电磁波。 声波能否通过真空传播？
    3. 声波可以建模为压力的变化。 为什么使用压力变化而不是实际压力？

    17.2 声速

    1. 原子的声音振动与热运动有何不同？
    2. 当声音从一种媒体传递到另一种媒介时，其传播速度不同，其频率或波长会发生变化吗？ 简要解释你的答案。
    3. 一个流行的派对技巧是吸入氦气，然后用高频、滑稽的声音说话。 解释一下这种现象。
    4. 你可能在实验室中使用了声波测距仪，通过声音传感器发出的点击声来测量物体的距离。 这个设备使用的原理是什么？
    5. 前面问题中讨论的声波测距仪通常需要校准。 在校准期间，软件会要求提供室温。 你认为为什么需要室温？

    17.3 声音强度

    1. 花样游泳队的六名成员佩戴耳塞以保护自己免受深处水压的影响，但他们仍然可以听到音乐并在水中完美演奏组合。 有一天，他们被要求离开游泳池，这样潜水队就可以练习几次潜水，他们尝试在垫子上练习，但似乎难度要大得多。 为什么会这样？
    2. 一个社区对将火车服务从城镇郊区带到市中心的计划感到担忧。 尽管火车站在街区之外，但目前的声强级别为市中心 70 dB。 市长向公众保证，市中心的声音差异仅为30 dB。 市民应该担心吗？ 为什么？

    17.4 站立声波的正常模式

    1. 你会得到两个相同长度的管乐器。 一个在两端都是开放的，而另一个在一端是封闭的。 哪个能产生最低频率？
    2. 泛音和谐波有什么区别？ 所有谐波都是泛音吗？ 所有的泛音都是谐波吗？
    3. 两个相同的柱子在两端开放，位于不同的房间里。 在房间 A 中，温度为 T = 20 °C，在 B 室中，温度为 T = 25 °C。每个电子管的末端都装有一个扬声器，使电子管以基频产生共振。 两个电子管的频率是否相同？ 哪个频率更高？

    17.5 音乐声音的来源

    1. 14。 一把未放大的吉他怎么会产生比用一根简单的棍子拉紧的弹弦更强烈的声音？
    2. 假设三根相同长度 (L) 的管道。 管道 A 的两端都是开放的，管道 B 的两端都是封闭的，管道 C 有一个开口端和一个封闭端。 如果三个电子管中的每个管的声速相同，那么在哪个管中可以产生最低的基频？ 在哪个电子管中可以产生最高的基频率？
    3. 管道 A 的长度为 L，两端均开放。 管道 B 有一定长度\(\frac{L}{2}\)，有一个开口端和一个封闭端。 假设两个电子管中的声速相同。 每个管中的哪个谐波是相等的？
    4. 两个实验室柱子之间用一根绳子绑在一起，相距为L的距离。 弦中的张力和线性质量密度使得弦上波浪的速度为 v = 343 m/s。具有对称边界条件的管的长度为 L，管中的声速为 v = 343 m/s。关于弦和管中谐波的频率可以说什么？ 如果字符串中的速度为 v = 686 m/s 怎么办？

    17.6 Beats

    1. 两个扬声器连接到变频信号发生器。 扬声器 A 产生 1.00 kHz 的恒定频率声波，扬声器 B 产生 1.10 kHz 的音调。 节拍频率为 0.10 kHz。 如果每个扬声器的频率加倍，产生的节拍频率是多少？
    2. 标签已经从音叉上刮掉了，你需要知道它的频率。 从它的大小来看，你怀疑它在 250 Hz 左右。 你会找到一个 250 赫兹的音叉和一个 270 赫兹的音叉。 当你敲击 250-Hz 的分叉和未知频率的分叉时，会产生 5 Hz 的节拍频率。 当你用 270 Hz 分叉击中未知事物时，节拍频率为 15 Hz。 未知频率是多少？ 你能只用 250-Hz 分叉推断出频率吗？
    3. 关于前面的问题，如果你只有250-Hz的分叉，你能想出一个办法来解决寻找未知频率的问题吗？ 21。 一辆 “艳丽” 的定制汽车有两个黄铜喇叭，它们本应产生相同的频率，但实际上发出的频率为263.8和264.5 Hz。 产生的节拍频率是多少？

    17.7 多普勒效应

    1. 多普勒移位是真的还是仅仅是一种感官错觉？
    2. 三个静止的观察者观察到多普勒偏移来自以恒定速度移动的声源。 观察员的驻扎情况如下所示。 哪个观察者会观察到最高频率？ 哪个观察者会观察到最低频率？ 关于观察者 3 观测到的频率可以说什么？

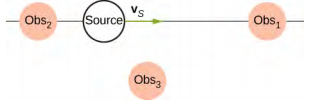
    Picture 是一幅移动源的图，它以恒定频率发出声波，恒定波长以声速移动。 源从静止观察点 2 移动到静止观察点 1，并在途中经过静止观察点 3 旁边。

    1. 下图显示的是静止的声源和移动的观察点。 描述观察者在此配置下观测到的频率

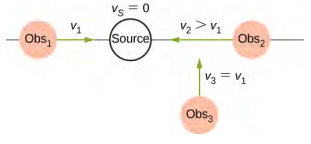
    Picture 是一幅静止声源的图，它以恒定频率发出声波，恒定波长以声速移动。 Observer one 以 v1 的速度向源移动，Observer 3 以相同的速度移动到距离源很近的点。 位于观察者 1 对面的 Observer 2 以 v1 的两倍的速度 v2 向源移动。

    1. 1980 年之前，天气预报员使用传统雷达。 20 世纪 60 年代，天气预报员开始尝试多普勒雷达。 你认为使用多普勒雷达有什么好处？

    17.8 冲击波

    1. 音爆和冲击波有什么区别？
    2. 出于与弓尾流相关的效率考虑，超音速运输机必须保持与声速（恒定马赫数）之比恒定的巡航速度。 如果飞机从暖空气飞向较冷的空气，它应该提高还是降低速度？ 解释你的答案。
    3. 当你听到音爆时，你往往看不见制造它的飞机。 这是为什么？

    问题

    1. 以使用方程 s (x, t) = 4.00 nm cos (3.66 m −1 x − 1256 s −1 t) 建模的声波为例。 声波的最大位移、波长、频率和速度是多少？
    2. 假设一个在空中移动的声波，其建模方程为 s (x, t) = 6.00 nm cos (54.9 3 m −1 x − 18.84 x 10 s −1 t)。 空气分子在 3.00 nm 和 —3.00 nm 之间移动所需的最短时间是多少？
    3. 以频率为 5.00 MHz 的诊断性超声波为例，用于检查软组织中的不规则性。 (a) 如果声速为 343 m/s，这种声波在空气中的波长是多少？ (b) 如果组织中的声速为 1800 m/s，则该波在组织中的波长是多少？
    4. 声波建模为\(\Delta\) P = 1.80 Pa sin（55.41 m −1 x − 18,840 s −1 t）。 声波的压力、波长、频率和速度的最大变化是多少？
    5. 声波使用波函数\(\Delta\) P = 1.20 Pa sin (kx − 6.28 x 10 4 s −1 t) 建模，声波以 v = 343.00 m/s 的速度在空气中传播。(a) 声波的波数是多少？ (b)\(\Delta\) P（3.00 m，20.00 秒）的值是多少？
    6. 声波中空气分子的位移是使用波函数 s (x, t) = 5.00 nm cos (91.54 m −1 x − 3.14 x 10 s −1 t) 建模的。 (a) 声波的波速是多少？ (b) 空气分子在简单的谐波运动中振荡时的最大速度是多少？ (c) 空气分子在简单的谐波运动中振荡时的最大加速度是多少？
    7. 扬声器放置在长水平管的开口处。 扬声器以 f 频率振荡，产生沿电子管向下移动的声波。 波浪以 v = 340.00 m/s 的速度穿过管道。声波使用波函数 s (x, t) = s ma x cos (kx −\(\omega\) t +) 建模\(\phi\)。 在时间 t = 0.00 s 时，x = 3.5 m 处的空气分子的最大位移为 7.00 nm。 同时，另一个位于 x = 3.7 m 的分子的位移为 3.00 nm。 扬声器振荡的频率是多少？
    8. 250-Hz 的音叉被敲击并开始振动。 声级计位于 34.00 米外。 声音\(\Delta\) t = 0.10 秒才能到达仪表。 音叉的最大排量为 1.00 mm。 为声音写一个波浪函数。
    9. 超声波换能器产生的在空气中移动的声波使用波动方程 s (x, t) = 4.50 nm cos (9.15 x 10 4 m −1 x − 2\(\pi\) (5.00 MHz) t) 建模。 该探头将用于无损检测，以测试钢梁的裂缝。 钢梁中的声速为 v = 5950 m/s。找到钢梁中声波的波函数。
    10. 海豚会发出用于导航的声波。 如果发出的声波的波长为 4.5 cm，水中的声速为 v = 1530 m/s，则声音的周期是多少？
    11. 蝙蝠利用声波捕捉昆虫。 蝙蝠可以检测高达 100 kHz 的频率。 如果声波以 v = 343 m/s 的速度在空气中传播，那么声波的波长是多少？
    12. 蝙蝠发出 100 kHz 的声波，声波以 v = 343 m/s 的速度在空气中传播。(a) 如果最大压差为 1.30 Pa，假设波浪是正弦波，那么什么波函数可以对声波进行建模？ （假设相移为零。） (b) 声波的周期和波长是多少？
    13. 以下图所示的压缩波图为例。 显示的是 t = 0.000 s（蓝色）和 t = 0.005 s（橙色）的波函数的快照。 压缩波的波长、最大位移、速度和周期是多少？

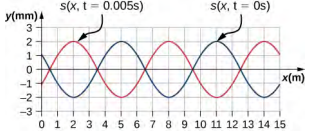
    图是一张显示压缩波的图形。 该波由两个正弦函数组成。 以蓝色显示的函数的最大值为 5、11，2、8、14 中的最小值。 以红色显示的函数的最大值为 2、8、14，5、11 中的最小值。

    1. 以前述压缩波问题中的图表为例。 显示的是 t = 0.000 s（蓝色）和 t = 0.005 s（橙色）的波函数的快照。 假设分子在时间 t = 0.00 s 且位置 x = 0.00 m 时的位移为 s (0.00 m, 0.00 s) = 1.08 mm，推导出一个波函数来对压缩波进行建模。
    2. 吉他弦以 100 Hz 的频率振荡并产生声波。 (a) 你认为振动弦产生的声波频率是多少？ (b) 如果声波的速度为 v = 343 m/s，则声波的波长是多少？

    17.2 声速

    1. 当被长矛戳时，歌剧女高音会发出 1200 Hz 的尖叫声。 如果声速为 345 m/s，它的波长是多少？
    2. 当声速为 340 m/s 时，哪个频率的波长为 0.10 米？
    3. 计算 1500-Hz 频率波长为 0.221 m 的某一天的声速。
    4. (a) 在 100 kHz 频率产生 5.96 厘米波长的介质中，声速是多少？ (b) 这可能是表17.1 中的哪种物质？
    5. 如文中所述，表明 20.0 °C 空气中的声速为 343 m/s。
    6. 撒哈拉沙漠的气温可以达到56.0°C（约134华氏度）。 在那个温度下，空气中的声速是多少？
    7. 海豚在空气和水中发出声音。 空气中声音的波长与其在海水中的波长的比率是多少？ 假设空气温度为 20.0 °C。
    8. 声纳回声在发射 1.20 秒后返回潜艇。 到产生回声的物体的距离是多少？ （假设潜艇在海里，而不是淡水中。）
    9. (a) 如果潜艇的声纳能够以 0.0100 秒的精度测量回波时间，那么它能探测到的最小距离差异是多少？ （假设潜艇在海里，而不是淡水中。） (b) 讨论这种时间分辨率对声纳系统探测产生回声的物体的大小和形状的能力施加的限制。
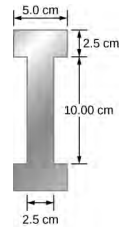
    10. 超声波通常用于无损检测方法。 例如，这种方法可用于查找建筑物中使用的钢工字梁中的结构缺陷。 以一根 10.00 米长的钢工字钢为例，其横截面如下所示。 I-Beam 的重量为 3846.50 N。工字光束中的声速是多少？ （Y 钢 = 200 GPa，\(\beta_{steel}\)= 159 GPa）。

    图片是一幅工字形光束的画。 中心杆长 10 厘米，厚 2.5 厘米。 两根宽5厘米、厚2.5厘米的平行杆连接到中心杆的两侧。

    1. 参加烟花汇演的物理学家计算了看见爆炸和听到爆炸声音之间的间隔，发现爆炸的时间为 0.400 秒。(a) 如果空气温度为 24.0 °C，并且你忽略了光线到达物理学家手中所需的时间，爆炸距离有多远？ (b) 考虑到光速，计算到爆炸的距离。 请注意，这个距离可以忽略不计。
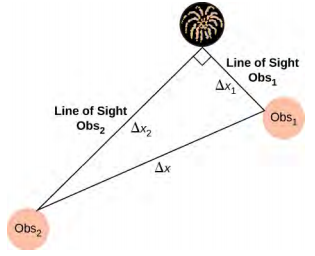
    2. 在 7 月 4 日的庆祝活动中，一支 M80 烟花在地面上爆炸，发出明亮的闪光和一声巨响。 夜间空气的温度为 T F = 90.00 °F。两名观察者看见闪光灯并听见爆炸声。 第一个观察者注意到闪光灯和爆炸之间的时间为 1.00 秒。 第二个观察者注意到差异为 3.00 秒。 两个观察者之间的视线以直角相交，如下所示。 两个观察者之间的距离\(\Delta\) x 是多少？

    图片是一幅由烟花源和两个观察者形成的三角形的画。 两个观察点之间的距离为 delta x。从第一个观察者到烟花源的视线为 delta x1。 从第二个观察者到烟花源的视线是 delta x2。

    1. 水样的密度为\(\rho\) = 998.00 kg/m 3，体积模量为\(\beta\) = 2.15 GPa。 通过样本的声速是多少？
    2. 假设蝙蝠使用声音回声来找到 3.00 米外的昆虫猎物。 （参见图 17.6。） (a) 计算 5.00 °C 和 35.0 °C 温度下的回波时间。(b) 这会导致蝙蝠在定位昆虫时的不确定性百分比是多少？ (c) 讨论这种不确定性的重要性以及它是否会给蝙蝠造成困难。 （实际上，蝙蝠在关闭时会继续使用声音，从而消除了这种效果和其他效果（例如猎物的运动）所带来的大部分困难。）

    17.3 声音强度

    1. 85.0 dB 声音的强度是多少（单位为瓦特/米的平方）？
    2. 割草机上的警告标签显示它产生的噪音水平为 91.0 dB。 以瓦特每平方米为单位是多少？
    3. 在空气中传播的声波的压力振幅为 0.5 Pa。 波浪的强度是多少？
    4. 前面问题中的声音对应于什么强度等级？
    5. 产生强度为 4.00 x 10 −2 W/m 2 的耳机产生的声强等级是多少（以 dB 为单位）？
    6. 强度是 90.0 dB 声音两倍的声音的分贝级别是多少？ (b) 强度为 90.0 dB 声音五分之一的声音的分贝级别是多少？
    7. 音量比 4.00 x 10 −9 W/m 2 声音低 7.00 dB 的声音的强度是多少？ (b) 比 4.00 x 10 −9-W/m 2 声音高 3.00 dB 的声音的强度是多少？
    8. 听力良好的人可以在 3000 Hz 的频率下感知低至 −8.00 dB 的声音。 这种声音的强度是多少，单位为瓦特每平方米？
    9. 如果距离你 3.0 米的大型家蝇发出 40.0 dB 的噪音，假设干扰的影响可以忽略不计，那么在该距离飞行 1000 的噪音水平是多少？
    10. 在动臂箱比赛中，十辆赛车围成一圈，在圆圈中心产生 120 dB 的声强级别。 假设干扰效果可以忽略，每个立体声音响在那里产生的平均声强级别是多少？
    11. 声波的振幅是根据其最大表压来测量的。 如果声强度上升 40.0 dB，声波的振幅会增加多少因素？
    12. 如果 1000 Hz 时 0 dB 的声强等级对应于 10 −9 atm 的最大表压（声幅），那么 60 dB 声音的最大表压是多少？ 120-dB 声音的最大表压是多少？
    13. 在 90.0 dB 的声强级别下暴露 8 小时可能会造成听力损伤。 在如此暴露的直径为 0.800 厘米的耳膜上，以焦耳为单位的能量是多少？
    14. 声音通过直接接触而不是通过空气传递到听诊器更有效，并且集中在耳膜的较小区域会进一步增强声音。 可以合理地假设，声音传送到听诊器的效率是通过空中传输的效率的100倍。 那么，听诊器的声音收集面积为15.0 cm 2，将声音集中在两个总面积为 0.900 cm 2 的耳膜上，效率为 40.0%，所产生的分贝增益是多少？
    15. 尽管扬声器的效率很低，但能量输入却非常小，却能产生强烈的声音。 计算直径为 12.0 厘米、效率为 1.00% 的扬声器产生 90.0dB 声强级别所需的功率输入。 （该值是扬声器处的声音强度级别。）
    16. 在耳朵可以反应的强度范围内，从阈值到短暂曝光后造成伤害的强度范围内，系数为10 -12，确实非常了不起。 如果你能用一台仪器测量相同范围内的距离，而你能测量的最小距离是 1 mm，那么最大的距离会是多少？
    17. 普通人能清楚区分出最接近 500 Hz 的频率与 500 Hz 的频率是多少？ 声音不是同时出现的。
    18. 如果电视的平均声强度从 70 到 73 dB，你能分辨出你的室友调高了电视上的声音吗？
    19. 如果女性需要放大阈值强度的 5.0 x 10 5 倍才能在所有频率下听见，那么她的总体听力损失是多少（以 dB 为单位）？ 请注意，较小的放大适合于更强烈的声音，以免她的听力因高于 90 dB 的电平而受到进一步损害。
    20. 在 100 Hz 时，一个人的听力阈值比正常水平高 10 dB，在 4000 Hz 时比正常水平高 50 dB。 如果这个人几乎听不见 100 Hz 的音调，那么 100-Hz 的音调必须比 4000-Hz 的音调强多少？

    17.4 站立声波的正常模式

    1. (a) 在声速为344 m/s的那一天，一根0.672米长的管子两端都开启的基频是多少？ (b) 它的二次谐波的频率是多少？
    2. 如果声速为 343 m/s，则基频为 176 Hz、第一个泛音为 352 Hz 的管的长度是多少？
    3. 耳道像一端闭合的管子一样产生共鸣。 （参见图 17.19。） 如果平均人群中耳道的长度在1.80到2.60厘米之间，那么基本共振频率的范围是多少？ 将空气温度设为37.0 °C，这与体温相同。
    4. 通过将空气温度设为 37.0 °C 来计算耳道中的第一个泛音，它像一端闭合的 2.40 厘米长的管子一样产生共鸣。耳朵对这种频率特别敏感吗？ （耳道的共振因其不均匀的形状而变得复杂，我们将忽略这一点。）
    5. 语音产生的一个粗略近似值是将呼吸通道和嘴巴视为一端封闭的共鸣管。 (a) 如果将空气温度设为 37.0 °C，如果管长 0.240 m，则基频是多少？ (b) 如果这个人用氦气代替空气，这个频率会变成多少？ 假设氦气和空气的温度依赖性相同。
    6. 在温度为 T = 22 °C 的房间里有一根 4.0 米长的管道，一端打开，一端封闭。能够产生可变频率的扬声器放置在开口端，用于使电子管产生共振。 (a) 基频的波长和频率是多少？ (b) 第一个泛音的频率和波长是多少？
    7. 在温度为 T = 25 °C 的房间里放置一根 4.0 米长的管道，两端都开放。能够产生可变频率的扬声器放置在开口端，用于使电子管产生共振。 (a) 基频的波长和频率是多少？ (b) 第一个泛音的频率和波长是多少？
    8. 尼龙吉他弦固定在两个相距 2.00 米的实验室柱子之间。 琴弦的线性质量密度为\(\mu\) = 7.20 g/m，其张力为 160.00 N。琴弦放置在一根管子旁边，两端均开口，长度为 L。琴弦被弹出，管子在 n = 3 模式下产生共振。 声速为 343 m/s。管子的长度是多少？
    9. 敲击 512 Hz 音叉并将其放置在带有可移动活塞的管子旁边，形成长度可变的管子。 当活塞距离开口端115.50 cm时，活塞向下滑动，达到共振。 当活塞距离开口端 82.50 厘米时，就会达到下一个共振。 (a) 电子管中的声速是多少？ (b) 活塞会在离开口端多远的地方产生下一个共振模式？
    10. 物理实验室的学生被要求找出一端封闭的管道中气柱的长度，其基频为 256 Hz。 他们垂直握住管子，在顶部装满水，然后在 256 Hz 音叉响起时降低水分，聆听第一次共振。 (a) 如果共振发生长度为 0.336 m，空气温度是多少？ (b) 他们将在多长时间内观察到第二次共振（第一次泛音）？

    17.5 音乐声音的来源

    1. 如果管乐器（例如大号）的基本频率为32.0 Hz，那么它的前三个泛音是什么？ 它的一端是封闭的。 （真正的大号的泛音比这个例子更复杂，因为它是一个锥形管。）
    2. 基频为 90.0 Hz 的低音管的前三个泛音是什么？ 它的两端都是开放的。 （真正的低音管的泛音比这个例子更复杂，因为它的双簧片使它更像一端封闭的管子。）
    3. 在气温为20.0°C的那一天，长笛需要多长时间才能使基频达到262 Hz（该频率对应于均匀回火色标上的中等摄氏度）？ 它的两端都是开放的。
    4. 在声速为 343 m/s 的那一天，双簧管需要多长才能产生 110 Hz 的基本频率？ 它的两端都是开放的。
    5. (a) 找出空气温度为18.0 °C时一端封闭的风琴管的长度，该管产生的基频为256 Hz。(b) 在25.0°C时它的基频是多少？
    6. 风琴管（L = 3.00 m）两端均已关闭。 计算前三种共振模式的波长和频率。 假设声速为 v = 343.00 m/s。
    7. 风琴管（L = 3.00 m）的一端是封闭的。 计算前三种共振模式的波长和频率。 假设声速为 v = 343.00 m/s。
    8. 频率为 2.00 kHz 的声波是由在 n = 6 模式下振荡的弦乐产生的。 弦的线性质量密度为\(\mu\) = 0.0065 kg/m，琴弦的长度为 1.50 m。琴弦的张力是多少？
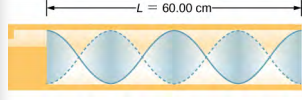
    9. 考虑一下通过使电子管产生共振所产生的声音，如下所示。 空气温度为 T C = 30.00 °C。产生的声音的波长、波速和频率是多少？

    图为 60 厘米长的管道中的波浪示意图。 一个管中有两个波长。 最大空气排量位于管道的末端。

    1. 学生拿着一根 80.00 厘米的实验杆，长度为杆子末端的四分之一。 实验杆由铝制成。 学生用锤子敲击实验室的杆子。 极点以尽可能低的频率产生共振。 那个频率是多少？
    2. 小提琴上的琴弦长度为 24.00 cm，质量为 0.860 g。琴弦的基本频率为 1.00 kHz。 (a) 琴弦上波浪的速度是多少？ (b) 琴弦中的张力是多少？
    3. 当空气温度从 10.0 °C 升至 30.0 °C 时，管乐器产生的频率会变化多少？ 也就是说，找到这些温度下的频率比率。

    17.6 Beats

    1. 存在哪些节拍频率：(a) 如果音符 A 和 C 一起演奏（频率为 220 和 264 Hz）？ (b) D 和 F 是否一起播放（频率为 297 和 352 Hz）？ (c) 如果所有四个都一起玩？
    2. 如果钢琴锤击中三根发出 127.8、128.1 和 128.3 Hz 频率的琴弦，会产生什么节拍频率？
    3. 钢琴调谐器在聆听 264.0 Hz 音叉和单根钢琴弦时，每 2.00 秒就会听到一个节拍。 字符串的两种可能频率是多少？
    4. 两端固定有两根相同的绳子，长度相同，为 2.00 m，线性质量密度为\(\mu\) = 0.0065 kg/m。 琴弦 A 的张力为 120.00 N。琴弦 B 的张力为 130.00 N。它们分别被弹出并在 n = 10 模式下发出声音。 节拍频率是多少？
    5. 钢琴调谐器使用 512 Hz 的音叉来调钢琴。 他敲下叉子然后敲钢琴上的琴键，听见 5 Hz 的节拍频率。 他收紧钢琴的琴弦，然后重复这个程序。 他再次听到 5 Hz 的节拍频率。 发生了什么？
    6. 线性质量密度为\(\mu\) = 0.0062 kg/m 的绳子在相距 1.30 米的两个柱子之间拉伸。 弦中的张力为 150.00 N。琴弦振荡并产生声波。 敲击 1024 赫兹的音叉，两个音源之间的节拍频率为 52.83 Hz。 弦上波浪的可能频率和波长是多少？
    7. 一辆汽车有两个喇叭，一个发出 199 Hz 的频率，另一个发出的频率为 203 Hz。 它们产生的节拍频率是多少？
    8. 钢琴的中间 C 锤击两根琴弦，产生 1.50 Hz 的节拍。 其中一根弦被调谐到 260.00 Hz。 另一根弦的频率是多少？
    9. 两个频率分别为 460 和 464 Hz 的音叉同时敲击。 你会听到什么平均频率，节拍频率是多少？
    10. 飞机上的双喷气发动机产生的平均声频为 4100 Hz，节拍频率为 0.500 Hz。 他们各自的频率是多少？
    11. 钢琴上相邻的三个按键（F、F-sharp 和 G）同时被敲击，产生的频率分别为 349、370 和 392 Hz。 这种不和谐的组合会产生什么节拍频率？

    17.7 多普勒效应

    1. (a) 看着迎面驶来的救护车以 110 km/h 的速度行驶并从警笛发出稳定的 800Hz 声音的人收到的频率是多少？ 这一天的声速为345 m/s。（b）救护车通过后她收到的频率是多少？
    2. (a) 在航展上，在声速为 342 m/s 的那一天，喷气式飞机以 1200 km/h 的速度直接飞向看台，发射频率为 3500 Hz。观察者收到的频率是多少？ (b) 当飞机直接飞离他们时，他们收到的频率是多少？
    3. 当一只鹰以 25.0 m/s 的速度飞向鼠标并发出频率为 3500 Hz 的尖叫声之前，鼠标接收到的频率是多少？ 将声速设为 331 m/s。
    4. 游行队伍中的观众从正在演奏 880-Hz 音符的迎面而来的小号手那里收到 888-Hz 的音调。 如果声速为 338 m/s，音乐家会以什么速度接近？
    5. 一列通勤列车在接近十字路口时会吹出 200 赫兹的喇叭。 声速为 335 m/s。(a) 在十字路口等候的观察者收到的频率为 208 Hz。 火车的速度是多少？ (b) 当火车离开时，观察者收到的频率是多少？
    6. 在声速为 344 m/s 的那一天，你能感觉到当你以 10.0 m/s 的速度向你拉动音叉时产生的频率变化吗？ 要回答这个问题，请计算频率偏移的系数，看看它是否大于 0.300%。
    7. 两只老鹰直接飞向对方，第一只以 15.0 m/s 的速度飞行，第二只以 20.0 m/s 的速度飞行。两只鹰都在尖叫，第一只发出 3200 Hz 的频率，第二只发出 3800 Hz 的频率。 如果声速为 330 m/s，他们会收到什么频率？
    8. 学生 A 以 v o = 5.00 m/s 的速度沿着学校的走廊奔跑，拿着一把响亮的 1024.00Hz 音叉朝着混凝土墙冲去。 声速为 v = 343.00 m/s。学生 B 站在墙边。 (a) 学生 B 听到的频率是多少？ (b) 学生 A 听到的节拍频率是多少？
    9. 一辆警笛（f = 1.00kHz）响起的救护车正在接近事故现场。 救护车以每小时 70.00 英里的速度移动。 一名护士正从相反的方向接近现场，以 v o = 7.00 m/s 的速度奔跑。护士观察到的频率是多少？ 假设声速为 v = 343.00 m/s。
    10. 救护车警笛的频率为900 Hz，正在接近你。 你站在拐角处，观察 960 Hz 的频率。 如果声速为 v = 340.00 m/s，救护车的速度是多少（以英里/小时为单位）？
    11. 信号源向你移动的最低速度是多少，才能听见它的频率被多普勒移动？ 也就是说，在声速为331 m/s的那一天，什么速度会产生0.300％的偏移？

    17.8 冲击波

    1. 一架飞机以 1.50 马赫的速度飞行，高度为 7500.00 米，其中声速为 v = 343.00 m/s。当观察者听到音爆时，飞机将离静止的观察者有多远？
    2. 在 8.50 km 高度飞行的喷气式飞机的速度为 2.00 马赫，其中声速为 v = 340.00 m/s。喷气式飞机直接进入头顶多久后，静止的观察者能听见音爆？
    3. 战斗机前部的冲击波角度为\(\theta\) = 70.00°。 喷气式飞机以 1200 km/h 的速度飞行。声速是多少？
    4. 一架飞机以 1.2 马赫的速度飞行，地面上的观察者在飞机直接进入头顶 15.00 秒后听到音爆。 飞机的高度是多少？ 假设声速为 vw = 343.00 m/s。
    5. 子弹发射后以 1342 英里/小时的速度移动。 假设声速为 v = 340.00 m/s。产生的冲击波的角度是多少？
    6. 扬声器放置在长水平管的开口处。 扬声器以 f 的频率振荡，产生沿电子管向下移动的声波。 波浪以 v = 340.00 m/s 的速度在管中移动。声波使用波函数 s (x, t) = s ma x cos (kx −\(\omega\) t +\(\phi\)) 建模。 在时间 t = 0.00 s 时，x = 2.3 m 处的空气分子的最大位移为 6.34 nm。 同时，另一个位于 x = 2.7 m 的分子的位移为 2.30 nm。 声波的波函数是什么，即找到波数、角频率和初始相移？
    7. 飞机以 1.2 马赫的速度移动并产生冲击波。 (a) 飞机的速度是多少（以米/秒为单位）？ (b) 冲击波移动的角度是多少？

    其他问题

    1. 两端都打开了一根 0.80 米长的管子。 空气温度为 26 °C。使用连接在信号发生器上的扬声器振荡管中的空气。 在电子管中产生共鸣的前两种声波模式的波长和频率是多少？
    2. 装满水的管子底部有一个阀门，允许水流出管道。 当水从管中排空时，气柱的长度 L 会发生变化。 在音管的开口处放置了一个 1024 赫兹的音叉。 水从管中排出，直到声波的 n = 5 模式产生共振。 如果房间内空气的温度为 18 °C，气柱的长度是多少？

    图为在装满水的管子开口上方放置一把音叉。 水从管中排出 L 的距离

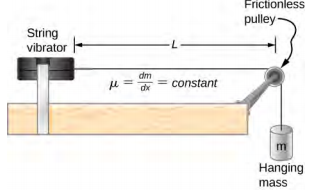
    1. 考虑下图。 弦式振动器和滑轮之间的弦长为 L = 1.00 m。弦的线性密度为\(\mu\) = 0.006 kg/m。弦式振动器可以以任何频率振荡。 悬挂质量为 2.00 千克。 (a) n = 6 模式的波长和频率是多少？ (b) 琴弦振荡琴弦周围的空气。 如果声音的速度为 v s = 343.00 m/s，声音的波长是多少？

    图中显示了连接到无摩擦滑轮的弦状振动器，悬挂质量为 m。将振动器连接到滑轮的绳子的距离为 L。

    1. 早期的多普勒移位实验是使用乐队在火车上演奏音乐进行的。 行驶中的铁路平板车上的小号手会弹奏320赫兹的音符。 静止的观察者在火车站台上听到的声波听到的频率为 350 Hz。 平板车的速度是多少（以英里/小时为单位）？ 空气的温度为 T C = 22 °C。
    2. 两辆汽车相互移动，两辆车都在敲响喇叭（f s = 800 Hz）。 汽车 A 以 65 英里/小时的速度行驶，汽车 B 的行驶速度为 75 英里/小时。 每个司机听到的节拍频率是多少？ 空气温度为 T C = 22.00 °C。
    3. 学生 A 在学生 B 之后跑步。学生 A 携带一个以 1024 Hz 的频率振铃的音叉，学生 B 携带一个 1000 Hz 的音叉振铃。 学生 A 以 v A = 5.00 m/s 的速度运行，学生 B 以 v B = 6.00 m/s 的速度运行。每个学生听到的节拍频率是多少？ 声速为 v = 343.00 m/s。
    4. 假设来自声源的声级为 75 dB，然后降至 52 dB，频率为 600 Hz。 确定 (a) 初始和 (b) 最终声强以及 (c) 初始和 (d) 最终声波振幅。 空气温度为 T C = 24.00 °C，空气密度为\(\rho\) = 1.184 kg/m 3。
    5. 多普勒雷达的多普勒偏移由 f = f R 确定\(\left(\dfrac{1 + v_{c}}{1 − v_{c}}\right)\)，其中 f R 是雷达的频率，f 是雷达观测到的频率，c 是光速，v 是目标的速度。 假设目标的速度比光速慢得多，在雷达上观察到的拍打频率是多少？
    6. 当声源接近时，静止的观察者听到的频率为 1000.00 Hz，在声源离开时听到的频率为 850.00 Hz。 声源以 75 英里/小时的恒定速度移动。 空气的温度是多少？
    7. 长笛演奏频率为 600 Hz 的音符。 长笛可以建模为两端开口的管道，长笛演奏者用手指位置改变长度。 如果这是基频，管的长度是多少？

    挑战问题

    1. 两个扬声器间隔一个距离 d，每个扬声器的发声频率为 f。观察者站在一个扬声器前，沿直线行走 x，垂直于两个扬声器，直到他达到第一个最大声音强度。 声速为 v 他离扬声器有多远？
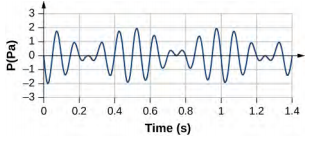
    2. 以下面显示的节拍为例。 这是位置 x = 0.00 m 的表压随时间的变化图。波浪以 v = 343.00 m/s 的速度移动。(a) 每秒有多少节拍？ (b) 波浪每秒振荡多少次？ (c) 将表压作为时间函数写入波函数。

    该图显示了以帕斯卡为单位的表压与时间（以秒为单位）绘制的表压。 这条线的波长较短，位于负 2 和正 2 帕斯卡之间 x 轴的上方和下方。

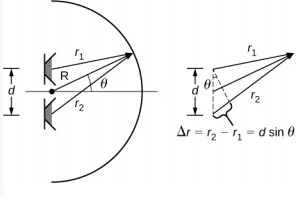
    1. 产生相同声音频率的两个扬声器之间的距离为 d。 假设沿着半径为 R 的圆的弧线，以扬声器的中点为中心，如下所示。 (a) 在什么角度会有最大值？ (b) 在什么角度会有最小值？

    图中显示了一个两边为 r1 和 2 的三角形。 三角形的高度为 6 米。 三角形底部的海拔将底部分成两部分，长度分别为2米和3米。 图为两个相距d的扬声器的图。 扬声器产生的声波在顶部扬声器的 r1 点和底部扬声器的 r2 点相交。 R 是从扬声器之间等距离的点到波浪交汇点的距离。 线路 R 形成角度 theta，直线垂直于连接两个扬声器的线。

    1. 绳子的长度为 1.5 m，线性质量密度\(\mu\) = 0.008 kg/m，张力为 120 N。如果空气温度为 T = 22 °C，管道两端开口的长度应该是多少，才能在 n = 3 模式下具有相同的频率？
    2. 琴弦（\(\mu\)= 0.006 kg/m，L = 1.50 m）固定在两端，张力为 155 N。它在 n = 10 模式下振荡并产生声音。 音叉在附近响起，产生的节拍频率为 23.76 Hz。 (a) 弦乐发出的声音的频率是多少？ (b) 如果音叉频率较低，音叉的频率是多少？ (c) 要使节拍频率为零，弦的张力应该是多少？
    3. 弦具有线性质量密度\(\mu\)，长度为 L，张力为 F T，并以 f 频率在 n 模式下振荡。找出张力稍有变化的比率。\(\frac{\Delta f}{f}\)
    4. 弦的线性质量密度\(\mu\) = 0.007 kg/m，长度 L = 0.70 m，张力为 F T = 110 N，并在 n = 3 模式下振荡。 (a) 振荡的频率是多少？ (b) 使用前面问题中的结果来找出张力增加 1.00% 时频率的变化。
    5. 由信号发生器供电的扬声器用于研究电子管中的谐振。 信号发生器可以从 1000 赫兹调整到 1800 赫兹的频率。 首先，研究了一根长度为0.75米、两端均开口的管子。 房间里的温度为 T F = 85.00 °F。(a) 可以研究管道的哪种正常模式？ 频率和波长是多少？ 接下来，在 0.75 米长的管道的一端盖上一个盖子。 (b) 可以研究管道的哪些正常模式？ 频率和波长是多少？
    6. 小提琴上的一根绳子长度为23.00厘米，质量为0.900克。 琴弦中的张力 850.00 N。房间里的温度为 T C = 24.00 °C。琴弦在 n = 9 模式下弹出并振荡。 (a) 琴弦上波浪的速度是多少？ (b) 产生的探空波长是多少？ (c) 振荡弦的频率是多少？ (d) 发出的声音的频率是多少？ (e) 产生的声音的波长是多少？

    贡献者和归因

    Template:ContribOpenStaxUni