17.9: 冲击波

Last updated
Save as PDF

Page ID: 204204

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

解释声震背后的机制
描述声震和冲击波之间的区别
描述一把弓醒过来

在讨论移动声源和静止观察者的多普勒效应时，我们考虑的唯一案例是声源以低于声速的速度移动的情况。回想一下，移动源接近静止观测器的观测频率为 f _o = f _s\(\left(\dfrac{v}{v - v_{s}}\right)\)。当声源接近声速时，观测到的频率就会增加。根据方程，如果声源以声速移动，则分母等于零，这意味着观测到的频率是无限的。如果声源以大于声速的速度移动，则观测到的频率为负。

这可能意味着什么？当声源接近声速时会发生什么？一些科学家曾经争辩说，如此大的压力波是声波的建设性干扰造成的，飞机不可能超过声速，因为压力足够大，足以摧毁飞机。但是现在飞机的飞行速度通常比声速快。 1976 年 7 月 28 日，埃尔登 ·W· 乔尔斯上尉和乔治 ·T· 摩根少校以 3529.60 km/h（2193.20 英里/小时）的速度驾驶洛克希德 SR-71 Blackbird #61 -7958，即 2.85 马赫。马赫数是声源的速度除以声速：

\[M = \frac{v_{s}}{v} \ldotp \label{17.21}\]

你会看到，当声源接近并超过声速时，就会出现有趣的现象。

多普勒效应和高速度

由接近甚至超过声速的移动源（例如喷气式飞机）发出的声音会怎样？这个问题的答案不仅适用于声音，也适用于所有其他波浪。假设一架喷气式飞机几乎直接冲向你，发出频率_{为 f s} 的声音。飞机的速度 v _s 越大，多普勒偏移越大，观测到的 f _o 值就越大（图\(\PageIndex{1}\)）。

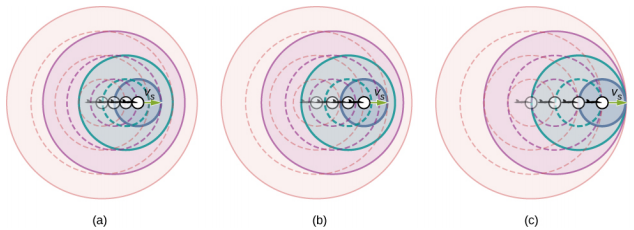
Picture 是一幅声源的画，它向静止的观察者移动并发出声波。 B 中的声源的移动速度比 A 中的声源更快。C 中的声源以声速移动，每个连续的波浪都会干扰前一个波浪，观察者同时观察到所有波浪。 — 图\(\PageIndex{1}\)：由于多普勒偏移，当移动源接近静止观测器时，观测到的频率高于源频率。光源移动得越快，观测到的频率就越高。在此图中，(b) 中的源的移动速度比 (a) 中的源移动得更快。显示的是四个时间步长，前三个时间步长显示为虚线。 (c) 如果声源以声速移动，则每个连续的波浪都会干扰前一个波浪，观察者会同时观察到所有声源。

现在，当 vs 接近声速时，fo 接近无穷大，因为 f _o = f _s 中的分母\(\left(\dfrac{v}{v \mp v_{s}}\right)\)接近零。以声速计算，此结果意味着在声源前方，每个连续的波浪都会干扰前一个波浪，因为声源以声速向前移动。观察者在同一时刻得到它们，因此频率是无限的 [图 (c) 部分]。

冲击波和声爆

如果声源超过声速，则在声源通过之前，观察者不会收到任何声音，因此来自接近声源的声音在后退时会与来自声源的声音混合。这种混音看起来很混乱，但发生了一些有趣的事情——冲击波产生了（图\(\PageIndex{2}\)）。

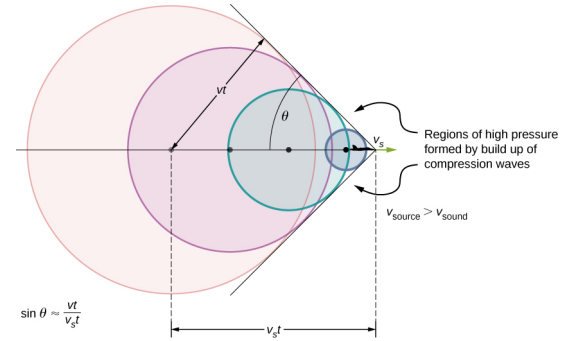
Picture 是一幅声源的图，该声源以比声速更快的速度向静止的观察者移动，并发出声波。声波从发射点开始以球形传播，但声源在每个波浪的前方移动。沿线的建设性干扰会产生冲击波。 — 图\(\PageIndex{2}\)：来自移动速度快于声速的声源的声波从其发射点以球形方式传播，但声源在每个波浪之前移动。沿着所示线条（实际上是三维圆锥体）的构造干扰会产生一种叫做音爆的冲击波。光源的速度越快，角度越小\(\theta\)。

同时到达那里的相似声波沿所示线条（三维圆锥体）产生构造干扰。这种叠加形成了一种叫做冲击波的干扰，这是一种由物体移动速度比声音更快产生的声音的构造干扰。在锥体内部，干扰主要是破坏性的，因此那里的声强比冲击波上的声强要小得多。冲击波的角度可以从几何图形中找到。在时间 t 中，声源移动了 v _s t，声波移动了一段距离 vt，可以使用 sin\(\theta\) = 找到角度\(\frac{vt}{v_{s} t} = \frac{v}{v_{s}}\)。请注意，马赫数的定义是\(\frac{v_{s}}{v}\)，角度的正弦等于马赫数的逆数，

\[\sin \theta = \frac{v}{w_{s}} = \frac{1}{M} \ldotp \label{17.22}\]

你可能听说过 “音爆” 这个常用术语。一个常见的误解是，音爆是在飞机突破声屏障时发生的；也就是说，加速到高于声速的速度。实际上，音爆是在冲击波沿着地面席卷时发生的。

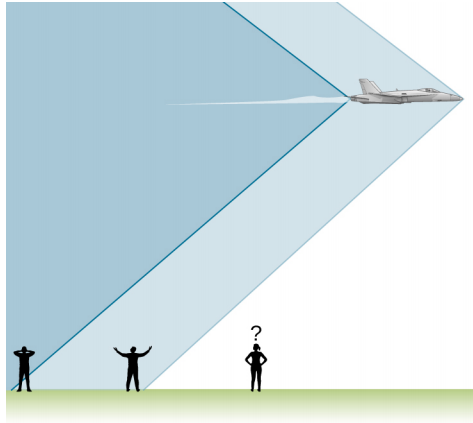
飞机产生两个冲击波，一个来自机头，另一个来自尾巴（图\(\PageIndex{3}\)）。在对航天飞机着陆的电视报道中，经常可以听到两个截然不同的轰鸣声。它们之间的间隔恰好与航天飞机通过某个点所花费的时间相隔。地面观察者通常看不到飞机在制造音爆，因为如图所示，它在冲击波到达他们之前就已经过去了。如果飞机在低空飞行，音爆中的压力可能会造成破坏，破坏窗户并使神经发抖。由于声震的破坏性很大，因此禁止在人口稠密地区上空进行超音速飞行。

图为观察者位于行驶中的飞机下方的图画。观察者经历了由飞机的机头和尾部产生的两次声爆。 — 图\(\PageIndex{3}\)：飞机经过后，在地面上观察到观察者经历的两次声爆，它们是由冲击波席卷地面时飞机的机头和尾部产生的

冲击波是称为弓醒的更广泛现象的一个例子。当波源的移动速度快于波浪传播速度时\(\PageIndex{4}\)，就会产生弓尾流，如图中的弓尾流。水浪从产生点开始绕圈散开，弓尾是熟悉的 V 形尾流，落后于源头。当亚原子粒子在介质中的传播速度快于光在该介质中的传播速度时，就会产生更具异国情调的弓尾声。（在真空中，最大光速为 c = 3.00×108 m/s；在水介质中，光速接近 0.75 摄氏度。）如果粒子在其通道中产生光线，则该光线在圆锥体上扩散，其角度表示粒子的速度，如图所示\(\PageIndex{5}\)。这种弓尾声被称为切伦科夫辐射，通常在粒子物理学中观察到。

一张鸭子在水中游泳并产生弓尾的照片。 — 人物\(\PageIndex{4}\)：由鸭子创建的弓尾声。建设性干扰会产生相当结构化的尾流，而尾流内部发生的波浪作用相对较少，干扰主要是破坏性的。（来源：Horia Varlan）

图为反应堆池中蓝光的照片。 — 图\(\PageIndex{5}\)：这个研究反应堆池中的蓝光是由亚原子粒子在水中的传播速度快于光速引起的切伦科夫辐射。（来源：美国核监管委员会）