Skip to main content
Global

17.8: 多普勒效应

  1. Last updated
  2. Save as PDF
  • Page ID
    204255

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    学习目标
    • 解释当移动的声源接近或离开静止的观察者时观测到的频率的变化
    • 解释观察者向或远离固定声源移动时观测到的频率的变化

    摩托车嗡嗡作响的特征声音就是多普勒效应的一个例子。 具体来说，如果你站在街角，观察到一辆有警笛声的救护车以恒定的速度驶过，你会注意到警笛声发生了两个典型的变化。 首先，当救护车接近时，声音的响度会增加，而当救护车离开时，声音的响度会降低，这是预料之中的。 但除此之外，高音警笛急剧转变为低音的声音。 当救护车经过时，静止的观察者听到的声音频率会从恒定的高频变为恒定的较低频率，尽管警笛产生恒定的源频率。 救护车越靠近，转变就越突然。 此外，救护车移动得越快，移位越大。 我们还听到了过往汽车、飞机和火车频率的这种典型变化。

    多普勒效应是由于声源或观察者的运动而导致观测到的声音频率的改变。 尽管不太熟悉，但对于静止的声源和移动的观察者来说，这种效果很容易注意到。 例如，如果你乘坐火车经过静止的警告喇叭，你会在经过时听到喇叭的频率从高变为低。 由于声源和观测器的相对运动而导致的频率的实际变化称为多普勒偏移。 多普勒效应和多普勒偏移以奥地利物理学家和数学家克里斯蒂安·约翰·多普勒（1803—1853 年）的名字命名，他用移动源和移动观测器进行了实验。 例如，多普勒让音乐家在行驶中的敞篷火车车厢上演奏，并在火车经过时站在火车轨道旁演奏。 在火车上和火车下都能观察到他们的音乐，并测量了频率的变化。

    导致多普勒偏移的原因是什么？ 该图\(\PageIndex{1}\)说明了静止和移动声源在静止空气团中发出的声波。 每种干扰都会从发出声音的点开始以球形方式扩散。 如果声源是静止的，则代表声波中空气压缩的所有球体都以同一点为中心，并且两侧的静止观察者听到的波长和频率与声源发射的波长和频率相同（案例 a）。 如果源在移动，情况就不同了。 空气的每次压缩都会在球体中从发射点向外移动，但发射点会移动。 这个移动的发射点使空气压缩在一侧靠得更近，另一侧相距更远。 因此，光源移动方向（案例 b 在右边）上的波长较短，相反方向的波长较长（案例 b 在左边）。 最后，如果观察者移动，如案例 (c)，他们接收压缩的频率就会改变。 向源移动的观察者以更高的频率接收它们，而离开源头的人以较低的频率接收它们。

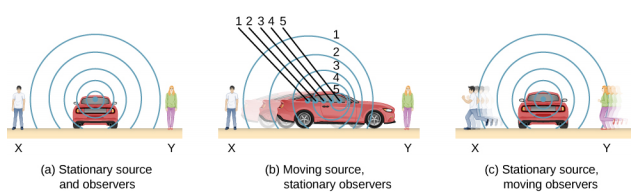
    图 A 是一幅画作，描绘了一辆停放的汽车是声波的来源，还有两个不行的人充当观察者。 图 A 是一幅作为声波来源的行驶中的汽车和两个不行驶的人作为观察者的画作。 图 C 是一幅作为声波来源的行驶中的汽车和两个作为观察者行驶的人的画作。
    图\(\PageIndex{1}\)：-声源发出的声音散布在球形波中。 (a) 当光源、观测器和空气处于静止状态时，所有方向和所有观察者的波长和频率都相同。 (b) 向右移动的声源发出的声音从发射点向外扩散。 波长减小，因此，频率在运动方向上增加，这样右边的观察者就会听到更高音调的声音。 对于左边的观察者来说，情况恰恰相反，那里的波长增加，频率降低。 (c) 当观察者相对于来源移动时，也会产生同样的效果。 向声源移动会增加频率，因为右边的观察者穿过的波峰比她静止时要多。 远离声源的运动会降低频率，因为左边的观察者穿过的波峰比静止时要少。

    我们知道波长和频率由 v = f 相关\(\lambda\)，其中 v 是固定的声速。 声音在介质中移动，无论声源是否移动，在该介质中具有相同的速度 v。 因此，f 乘以\(\lambda\)是一个常数。 因为如果 (b) 接收的波长较短，则右边的观察者接收的频率必须更高。 同样，左边的观察者接收的波长更长，因此他听到的频率较低。 案例 (c) 也会发生同样的情况。 向源移动的观测器接收的频率较高，而远离源的观察者接收到的频率较低。 因此，一般而言，信号源和观察器彼此之间的相对运动会增加接收频率。 相对运动分开会降低频率。 相对速度越大，效果越大。

    多普勒效应不仅适用于声音，而且当观察者和声源之间存在相对运动时，任何波浪都会产生多普勒效应。 例如，声波、光波和水波的频率会发生多普勒偏移。 多普勒移位可用于确定速度，例如在医疗诊断中何时从血液中反射超声波。 恒星和星系的相对速度由从它们接收的光频率的变化决定，这在很大程度上暗示了宇宙的起源。 对多普勒偏移的观测深刻影响了现代物理学。

    多普勒偏移导致的观测频率导出

    以图中的两个静止观测器 X 和 Y 为例\(\PageIndex{2}\)，它们位于静止源的两侧。 每个观察者听到的频率相同，该频率是固定声源产生的频率。

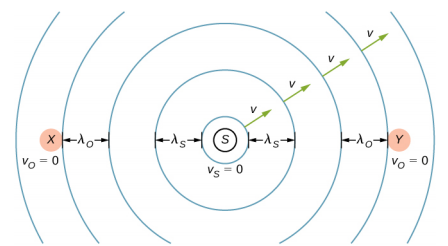
    Picture 是一幅静止声源的图，它以恒定频率发出声波，以声速发出恒定波长。 两个静止的观察者在声源两侧记录波浪。
    图\(\PageIndex{2}\)：固定声源以恒定频率 f s、恒定波长\(\lambda_{s}\)、声速发出声波 v 两个固定观测器 X 和 Y 在声源两侧观测频率 fo = f s，波长为一个\(\lambda_{o} = \lambda_{s}\)。

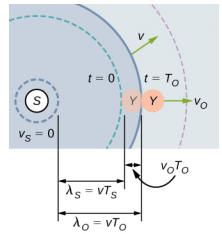
    现在假设一个静止的观测器 X，其光源以恒定速度 v s < v 移开观察者（图\(\PageIndex{3}\)）。 在时间 t = 0 时，声源发出以黑色表示的声波。 该波以声速 v 向外移动。周期 T s 的每个时间间隔声波的位置显示为虚线。 一段时间后，声源移动\(\Delta\) x = v s T s 并发出第二个声波，该声波以声速移出。 声源继续移动并产生声波，如编号为 3 和 4 的圆圈所示。 请注意，当波浪向外移动时，它们保持在各自的原点居中。

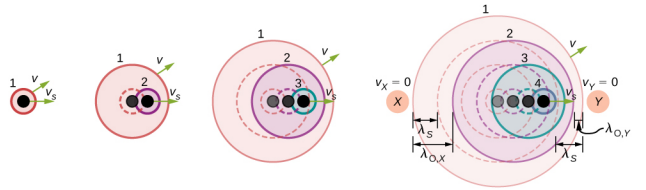
    Picture 是一幅声源的画，它以恒定的速度移动，远离静止的观察者并发出声波。
    图\(\PageIndex{3}\)：声源以恒定速度移动而不是远离观察者 X。移动的声源以恒定频率 f s、恒定波长\(\lambda_{s}\)、声速发出声波 v 以 T s 间隔的声源快照显示为声源远离静止观察点 X。实线表示声波在自初始时间起四个周期后的位置。 虚线用于显示波浪在每个时间段的位置。 观察者听到的波长为\(\lambda_{o} = \lambda_{s} + \Delta x = \lambda_{s} + v_{s}T_{s}\)。

    利用波长等于速度乘以周期，周期与频率相反的事实，我们可以推导出观测到的频率：

    \[\begin{align} \lambda_{o} & = \lambda_{s} + \Delta x \\ vT_{o} & = vT_{s} + v_{s} T_{s} \\ \dfrac{v}{f_{o}} & = \dfrac{v}{f_{s}} + \dfrac{v_{s}}{f_{s}} = \dfrac{v + v_{s}}{f_{s}} \\ f_{o} & = f_{s} \left(\dfrac{v}{v + v_{s}}\right) \ldotp \end{align}\]

    当声源远离观察者时，观测到的频率低于源频率。

    现在假设一个声源以恒定速度 v s 移动，向静止观察点 Y 移动，如图所示\(\PageIndex{3}\)。 波长由 Y 观测为\(\lambda_{o} = \lambda_{s} − \Delta x = \lambda_{s} − v_{s} T_{s}\)。 再一次，利用波长等于速度乘以周期，周期与频率相反的事实，我们可以推导出观测到的频率：

    \[\begin{split} \lambda_{o} & = \lambda_{s} - \Delta x \\ vT_{o} & = vT_{s} - v_{s} T_{s} \\ \dfrac{v}{f_{o}} & = \dfrac{v}{f_{s}} - \dfrac{v_{s}}{f_{s}} = \dfrac{v - v_{s}}{f_{s}} \\ f_{o} & = f_{s} \left(\dfrac{v}{v - v_{s}}\right) \ldotp \end{split}\]

    当光源移动且观察者处于静止状态时，观测到的频率为

    \[f_{o} = f_{s} \left(\dfrac{v}{v \mp v_{s}}\right), \label{17.18}\]

    其中 f o 是静止观察者观测到的频率，f s 是移动源产生的频率，v 是声速，v s 是声源的恒定速度，顶部符号代表接近观察者的声源，底部符号代表消息来源偏离了观察者。

    如果观察者在移动而光源处于静止状态会发生什么？ 如果观察者向静止源移动，则观测到的频率高于源频率。 如果观察者正在远离静止光源，则观测到的频率低于源频率。 以图中的观察者 X\(\PageIndex{4}\) 为例，观察者以 v o 的速度向静止源移动。 源发出的音调具有恒定频率 f s 和恒定周期 T s。 观察者听到信号源发出的第一波波。 如果观察者处于静止状态，则一个波长的声音通过的时间应等于声源 T s 的周期。 由于观察者正在向源移动，因此一个波长通过的时间小于 T s，等于观测周期 T o = T s −\(\Delta\) t。在时间 t = 0 时，观察者从一个波长的起点开始，向第二个波长移动波长从光源移出。 波长等于观察者行进的距离加上声波在观察者遇到之前传播的距离：

    \[\begin{split} \lambda_{s} & = vT_{o} + v_{o} T_{o} \\ vT_{s} & = (v + v_{o}) T_{o} \\ v \left(\dfrac{1}{f_{s}}\right) & = (v + v_{o}) \left(\dfrac{1}{f_{o}}\right) \\ f_{o} & = f_{s} \left(\dfrac{v + v_{o}}{v}\right) \ldotp \end{split}\]

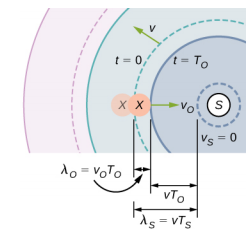
    Picture 是一幅静止声源的图，它以恒定频率发出声波，恒定波长以声速移动。 观察者 X 以恒定速度向源移动。
    图\(\PageIndex{4}\)：固定声源发射频率恒定 f s 的声波，恒定波长以声速\(\lambda_{s}\)移动 v Observer X 以恒定速度 v o 向声源移动，图中显示了观察者的初始和最终位置X. 观察器 X 观察到的频率高于源频率。 实线显示波浪在 t = 0 处的位置。 虚线显示波浪在 t = T o 处的位置。

    如果观察者正在远离光源（图\(\PageIndex{5}\)），则可以找到观测到的频率：

    \[\begin{split} \lambda_{s} & = vT_{o} - v_{o} T_{o} \\ vT_{s} & = (v - v_{o}) T_{o} \\ v \left(\dfrac{1}{f_{s}}\right) & = (v - v_{o}) \left(\dfrac{1}{f_{o}}\right) \\ f_{o} & = f_{s} \left(\dfrac{v - v_{o}}{v}\right) \ldotp \end{split}\]

    图片是一幅静止声源的图，它以恒定频率发射声波，恒定波长以声速移动。 观察者 X 以恒定速度移开信号源。
    图\(\PageIndex{5}\)：固定声源发出频率恒定 f s 的声波，恒定波长以声速\(\lambda_{s}\)移动 v Observer Y 以恒定速度 v o 离开声源，图中显示了声源的初始和最终位置观察者 Y. 观察者 Y 观察到的频率低于源频率。 实线显示波浪在 t = 0 处的位置。 虚线显示波浪在 t = T o 处的位置。

    观察者朝向或远离静止源的方程可以合并为一个方程：

    \[f_{o} = f_{s} \left(\dfrac{v \pm v_{o}}{v}\right), \label{17.19}\]

    其中 f o 是观测频率，f s 是源频率，v 是声速，v o 是观察者的速度，顶部符号表示观察者接近声源，底部符号代表观察者离开声源。 方程\ ref {17.18} 和方程\ ref {17.19} 可以概括为一个方程（顶部符号表示接近）\(\PageIndex{1}\)，并在表中进一步说明，其中 f o 是观测频率，f s 是声速，v o 是声速观察者，v s 是源的速度，顶部的标志代表接近，底部的标志代表离开。

    \[f_{o} = f_{s} \left(\dfrac{v \pm v_{o}}{v \mp v_{s}}\right), \label{17.20}\]

    桌子\(\PageIndex{1}\)
    多普勒移位\(f_{o} = f_{s} \left(\dfrac{v \pm v_{o}}{v \mp v_{s}}\right)\) 静止观察者 观察者向源移动 观察者正在远离源头
    \ (f_ {o} = f_ {s}\ 左 (\ dfrac {v\ pm v_ {o}} {v\ mp v_ {s}}\ 右) “>固定源 $$f_ {o} = f_ {s}\ nonumber $$ $$f_ {o} = f_ {s}\ 左 (\ dfrac {v + v_ {o}} {v}\ 右)\ nonumber $$ $$f_ {o} = f_ {s}\ 左 (\ dfrac {v-v_ {o}} {v}\ 右)\ nonumber $$
    \ (f_ {o} = f_ {s}\ 左 (\ dfrac {v\ pm v_ {o}} {v\ mp v_ {s}}\ 右) “>Source 向观察者移动 $$f_ {o} = f_ {s}\ 左 (\ dfrac {v} {v-v_ {s}}\ 右)\ nonumber $$ $$f_ {o} = f_ {s}\ 左 (\ dfrac {v + v_ {o}} {v-v_ {s}}\ 右)\ nonumber $$ $$f_ {o} = f_ {s}\ 左 (\ dfrac {v-v_ {o}} {v-v_ {s}}\ 右)\ nonumber $$
    \ (f_ {o} = f_ {s}\ 左 (\ dfrac {v\ pm v_ {o}} {v\ mp v_ {s}}\ 右) “>Source 正在远离观察者 $$f_ {o} = f_ {s}\ 左 (\ dfrac {v} {v + v_ {s}}\ 右)\ nonumber $$ $$f_ {o} = f_ {s}\ 左 (\ dfrac {v + v_ {o}} {v + v_ {s}}\ 右)\ nonumber $$ $$f_ {o} = f_ {s}\ 左 (\ dfrac {v-v_ {o}} {v + v_ {s}}\ 右)\ nonumber $$
    注意

    多普勒效应涉及运动，该视频将有助于可视化移动的观察者或信号源的效果。 该视频显示了一个移动的源和一个静止的观察点，以及一个移动的观察点和一个静止的观察点。 它还讨论了多普勒效应及其在光中的应用。

    示例\(\PageIndex{1}\): Calculating a Doppler Shift

    假设一列带有 150 Hz 喇叭的列车在声速为 340 m/s 的那一天在静止空气中以 35.0 m/s 的速度移动。

    1. 火车驶近和经过后，静止的人在轨道旁观察到的频率是多少？
    2. 列车的工程师在列车上行驶时观察到的频率是多少？

    策略

    要在 (a) 中找到观测到的频率，我们必须使用 f ob s = f s，\(\left(\dfrac{v}{v \mp v_{s}}\right)\)因为源在移动。 减号用于驶近的列车，加号用于后退的列车。 在 (b) 中，有两个多普勒移位——一个用于移动源，另一个用于移动的观察者。

    解决方案

    1. 在 f o = f s 中输入已知值\(\left(\dfrac{v}{v - v_{s}}\right)\)：$$f_ {o} = f_ {s}\ 左 (\ dfrac {v} {v-v_ {s}}\ 右) = (150\; Hz)\ 左 (\ dfrac {340\; m/s} {340\; m/s}\ 右)\ ldotp$$计算静止人物观测到的频率为火车驶近：$$f_ {o} = (150\; Hz) (1.11) = 167\;Hz\ ldotp$$使用带加号的相同方程来计算火车后退时静止的人听到的频率：$$f_ {o} = f_ {s}\ 左 (\ dfrac {v} {v + v_ {s}}\ 右) = (150\; Hz)\ 左 (\ dfrac {340\; m/s} {340\; m/s\ 35.0\; m/s}\ right)\ ldotp$$计算第二个频率：$$f_ {o} = (150\; Hz) (0.907) =136\; Hz\ ldotp$$
    2. 识别已知数：
      • 工程师接收的频率与号角发射的频率相同，这似乎是合理的，因为它们之间的相对速度为零。
      • 相对于介质（空气），速度为 v s = v o = 35.0 m/s。
      • 第一个多普勒移位用于移动的观察者；第二个用于移动源。

    使用以下方程：

    \[f_{o} = \left[ f_{s} \left(\dfrac{v \pm v_{o}}{v}\right) \right] \left(\dfrac{v}{v \mp v_{s}}\right) \ldotp\]

    方括号中的量是由于观察器移动而产生的多普勒移位频率。 右边的因子是移动源的影响。 因为列车工程师正朝着喇叭的方向移动，所以我们必须使用加号表示 v obs；但是，由于喇叭也朝着远离工程师的方向移动，所以我们也使用加号表示 v s。 但是火车以相同的速度运载工程师和喇叭，所以 v s = v o。 结果，除了 f s 之外的所有东西都取消了，产生

    \[f_{o} = f_{s} \ldotp\]

    意义

    对于源和观察者不一起移动的情况，当源（在本例中为列车）距离足够远以至于运动几乎沿着连接源和观察者的线路移动时，计算出的数字是有效的。 在这两种情况下，这种变化都是显著的，很容易注意到。 请注意，朝向运动的偏移为 17.0 Hz，向外移动的移位为 14.0 Hz。 这些变化是不对称的。

    对于乘坐列车的工程师来说，由于信号源和观测器一起移动，我们可以预期频率不会发生变化。 这符合你的经验。 例如，摩托车驾驶员和乘客之间的对话频率没有多普勒变化。 当风在他们之间移动空气时，人们说话时也会观察到对话中没有多普勒移动。 关键在于，源和观察者之间没有相对移动。

    练习 17.9

    描述一下你生活中的一种情况，你可能会依靠多普勒换档来帮助你，无论是在开车时还是在交通附近行走。

    多普勒效应和多普勒偏移在科学和工程中有许多重要的应用。 例如，超声波中的多普勒偏移可用于测量血速，而警察则使用雷达（微波）中的多普勒偏移来测量汽车速度。 在气象学中，多普勒偏移用于跟踪暴风云的运动；这样的 “多普勒雷达” 可以给出天气前沿雨雪的速度和方向。 在天文学中，我们可以检查遥远星系发出的光并确定它们相对于我们星系的速度。 当星系远离我们时，它们的光会转移到较低的频率，从而转移到更长的波长，即所谓的红移。 这些来自遥远星系的信息使我们能够估计宇宙的年龄（来自宇宙大爆炸）约为140亿年。