Skip to main content
Global

17.7: Beats

  1. Last updated
  2. Save as PDF
  • Page ID
    204254

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    学习目标

    • 确定两个频率不同的声波产生的节拍频率
    • 描述乐器是如何产生节拍的

    音乐研究提供了许多例子，说明波浪的叠加以及由此产生的建设性和破坏性干扰。 演奏音乐的例子很少，只有一个音源在很长一段时间内播放单个频率。 你可能会同意，长时间发出单一频率的声音可能很无聊到刺激的地步，就像飞机发动机或响亮的风扇中不需要的无人机一样。 由于混合了各种乐器和声音不断变化的频率，音乐既愉悦又有趣。

    由于两个或更多声音频率的建设性和破坏性干扰而发生的一种有趣现象是节拍现象。 如果两个声音的频率不同，则声波可以建模为

    \[y_{1} = A \cos (k_{1} x - 2 \pi f_{1} t)\]

    和

    \[\; y_{2} = A \cos (k_{2} x - 2 \pi f_{2} t) \ldotp \nonumber\]

    使用三角恒等式

    \[\cos u + \cos v = 2 \cos \left(\dfrac{u + v}{2}\right) \cos \left(\dfrac{u − v}{2}\right)\]

    将太空中的点视为\(x = 0.0\, m\)，我们发现在太空中某一点通过两个声波的叠加产生的声音等于图\(\PageIndex{1}\)：

    \[y(t; x=0\,m) = 2A \cos (2 \pi f_{avg} t) \cos \left[ 2 \pi \left(\dfrac{|f_{2} - f_{1}|}{2}\right) t \right], \nonumber\]

    节拍频率在哪里

    \[f_{beat} = |f_{2} - f_{1}| \ldotp \label{17.17}\]

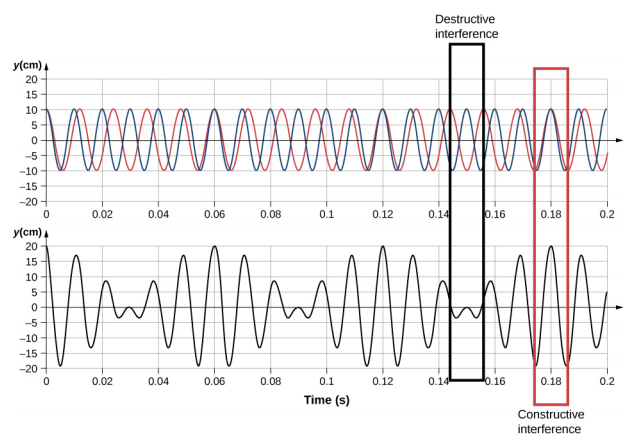
    图表以厘米为单位绘制位移与时间（以秒为单位）。 上图显示了两个声波。 下图显示了干扰波，其中显示了构造（双强度）和破坏性（零强度）区域。
    图\(\PageIndex{1}\)：两个不同频率的声波的建设性和破坏性干扰所产生的节拍。

    钢琴调谐器可以使用这些节拍来调钢琴。 敲打音叉，然后在钢琴上弹奏音符。 当钢琴调谐器调弦时，节拍的频率会降低，因为演奏的音符的频率接近音叉的频率。

    示例\(\PageIndex{1}\): Find the Beat Frequency Between Two Tuning Forks

    当同时敲击频率为 256 Hz 的音叉和频率为 512 Hz 的音叉时，产生的节拍频率是多少？ 策略节拍频率是两个频率的差。

    解决方案

    我们使用方程\ ref {17.17} 来获取节拍频率

    \[f_{beat} = |f_2 − f_1| = (512 - 256)\; Hz = 256\; Hz \ldotp \nonumber \]

    意义

    节拍频率是两个频率之间差值的绝对值。 负频率是没有意义的。

    练习\(\PageIndex{1}\)

    如果两个以上的频率相互作用会发生什么？ 考虑三个频率。

    除了研究声音之外，对各种波浪叠加的研究还有许多有趣的应用。 在后面的章节中，我们将讨论粒子的波浪特性。 粒子可以建模为 “波包”，它是由各种波浪的叠加产生的，其中粒子以波包的 “群速度” 移动。