17.6：音乐声音的来源

Last updated
Save as PDF

Page ID: 204187

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

描述仪器中的共振频率，这些仪器可以建模为具有对称边界条件的管道
描述仪器中的谐振频率，这些仪器可以建模为具有反对称边界条件的管道

某些乐器，例如木管乐器、铜管风琴和管风琴，可以建模为具有对称边界条件的管道，即要么两端都开启，要么两端都闭合（图$\PageIndex{1}$）。其他仪器可以建模为具有反对称边界条件的管道，例如一端开口而另一端封闭的管道（图$\PageIndex{2}$）。

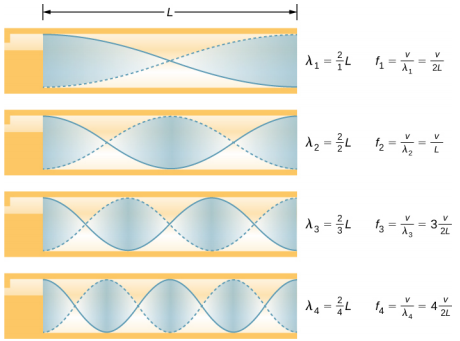
图为一端封闭的管道的基本声和三个最低泛音的示意图。基本波长的一半在管中。第一个泛音在管中有一个波长，第二个泛音在管中有一个波长，第三个泛音有两个波长在管中。所有管道两端的空气排量都最大。 — 图$\PageIndex{1}$：有些乐器可以建模为两端开口的管道。

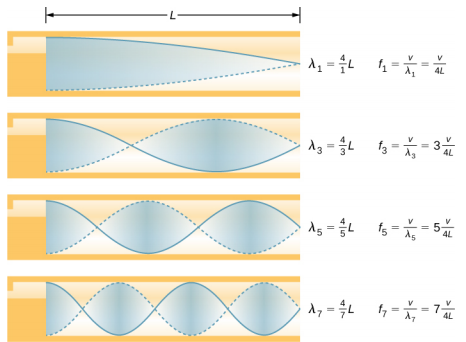
图为一端封闭的管道的基本声和三个最低泛音的示意图。基础波长的四分之一在管中。第一个泛音在电子管中有四分之三的波长，第二个泛音在管道中有四分之五的波长，第三个泛音的四分之七波长在管中。它们一端都有最大排气量，封闭端没有排气量。 — 图$\PageIndex{2}$：有些乐器可以建模为一端封闭的管道。

共振频率是由纵向波产生的，这些纵波沿着管道向下传播，干扰反射波朝相反方向传播。管风琴是用各种固定长度的管道制造的，以产生不同的频率。波浪是允许压缩空气在管道中膨胀的结果。即使在开放的管道中，由于管道侧面的限制和开口管外的大气压力，也会发生一些反射。

抗阳极不出现在管道开口处，而是取决于管道的半径。波浪只有在管的开口端之外才会完全膨胀，对于薄壁管，应增加末端校正。该端部校正大约是管道半径的0.6倍，应加到管道长度上。

长笛或双簧管等乐器的演奏者通过打开和关闭手指孔来改变管子的长度。在长号上，您可以使用滑动管更改管长。号角的长度是固定的，只能产生有限的频率范围。

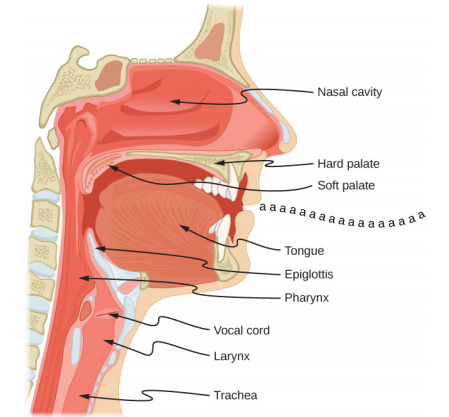
基本音和泛音可以以多种组合同时出现。例如，小号上的中间 C 听起来与单簧管上的中间 C 有明显的不同，尽管两种乐器都是一端封闭的管子的修改版本。基本频率是相同的（通常是最强烈的），但是泛音及其强度混合是不同的，并且会受到音乐家的阴影。这种混音赋予了各种乐器（和人声）独特的特征，无论它们是空中柱、弦乐、发声箱还是鼓头。实际上，我们的大部分言语都是通过塑造喉咙和嘴巴形成的空腔，以及定位舌头以调整基本和泛音组合来决定的。例如，可以使简单的共振腔与元音产生共鸣（图$\PageIndex{3}$）。在青春期的男孩中，喉部会长大，共振腔的形状发生变化，这就导致了男女之间主要说话频率的差异。

图为口腔和喉部系统的示意图。空气从气管传播到喉部、咽部和嘴巴。声带位于喉部和咽部之间。会厌位于咽部上方。舌头位于嘴里。口感柔软。硬腭将口腔与鼻腔分开。 — 图$\PageIndex{3}$：喉部和嘴巴形成一端封闭的气柱，根据语音箱中的振动产生共振。泛音的频谱及其强度因嘴巴形状和舌头位置而异，形成不同的声音。语音箱可以用机械振动器代替，而且语音仍然可以理解。基本形状的变化使不同的声音易于识别。

示例 17.6：计算基波为 128 Hz 的管道长度

(a) 如果在空气温度为22.0°C的那一天，如果管道的基频为128 Hz（低于中温摄氏度），那么一端封闭的管道应该有多长？ (b) 第四次泛音的频率是多少？

策略

长度 L 可以从 f _n = 的关系中找到$n \frac{v}{4L}$，但我们首先需要找到声速 v。

解决方案

识别已知数：基频为 128 Hz，空气温度为 22.0 °C。使用 f _n =$n \frac{v}{4L}$ 找出基频 (n = 1)，$$f_ {1} =\ frac {v} {4L}\ ldotp$求解这个长度方程，$$L =\ frac {v} {4f_ {1}}\ ldotp$$使用 v = (331 m/s)$\sqrt{\frac{T}{273\; K}}$，$$v = (331\; m/s)\ sqrt {\ frac {295\; K} {273\; K}} = 344\; m/s\ ldotp$$在 L.$L =\ frac {v} {4f_ {1}} =\ frac {344\; m/s} {4\ (128); Hz)} =0.672\; m$$
识别已知数：第一个泛音有 n = 3，第二个泛音有 n = 5，第三个泛音有 n = 7，第四个泛音有 n = 9。将第四个泛音的值输入到 f _n =$n \frac{v}{4L}$，$$f_ {9} = 9\ frac {v} {4L} = 9 f_ {1} = 1.15\; kHz\ ldotp$$

意义

许多管乐器都是经过改良的管子，有指孔、阀门和其他装置，用于改变共振气柱的长度，从而改变音符的演奏频率。产生非常低频率的喇叭需要很长的电子管，以至于它们会被盘绕成环路。大号就是一个例子。泛音是出现在简单的管子还是乐器中，取决于其振动的刺激方式及其形状的细节。例如，长号不会产生其基本频率，只会发出泛音。

如果你有两个具有相同基频的电子管，但其中一个在两端都是开放的，另一个在一端是封闭的，那么它们在播放时听起来会有所不同，因为它们的泛音不同。例如，在开放的管子上播放中间 C 听起来会更丰富，因为它有基数和奇数的偶数倍数。封闭的管子只有奇数倍数。

共振

共振发生在许多不同的系统中，包括弦束、气柱和原子。正如我们在前面的章节中所讨论的那样，共振是系统在其固有频率下的驱动或强制振荡。在共振时，能量被迅速传递到振荡系统，其振荡幅度会增加，直到胡克定律无法再描述该系统。这方面的一个例子是某些类型的摇滚音乐中故意产生的失真声音。

管乐器使用气柱中的共振来放大嘴唇或振动簧片发出的音调。其他乐器也巧妙地使用空气共振来放大声音。图中$\PageIndex{4}$显示的是小提琴和吉他，两者都有发声箱，但形状不同，因此泛音结构不同。振动弦产生一种在发声箱中产生共鸣的声音，极大地放大了声音并产生了泛音，赋予了乐器独特的音色。发声箱的形状越复杂，它在很宽的频率范围内产生共振的能力就越大。马林巴，如图所示$\PageIndex{5}$，使用木板条下方的花盆或葫芦来放大其色调。锅的共振可以通过加水来调节。

图 A 是小提琴的特写照片。图 B 是一个人弹吉他的照片。 — 图$\PageIndex{4}$：诸如（a）小提琴和（b）吉他之类的弦乐器在发声箱中使用共振来放大和丰富振动弦产生的声音。琴桥和支架将弦的振动耦合到发声箱和里面的空气。（来源 a：费利西亚诺·吉马雷斯对作品的修改；来源 b：史蒂夫·斯诺德格拉斯对作品的修改）

两位音乐家在马林巴舞上演奏的照片。 — 图$\PageIndex{5}$：自史前时代以来，共振就被用于乐器中。这款 marimba 使用葫芦作为共振室来放大声音。（来源：“APC 活动” /Flickr）

我们在讨论共振和驻波时强调了声音的应用，但是这些想法适用于任何具有波浪特性的系统。例如，振动弦实际上会产生共鸣，其基本原理和色彩与气柱相似。更微妙的是原子中的共振，这是由于其电子的波浪特性造成的。它们的轨道可以看作是驻波，具有基态（基态）和泛音（激发态）。令人着迷的是，波浪特性适用于如此广泛的物理系统。