17.5:站立声波的正常模式
- Page ID
- 204201
- 解释降音耳机背后的机制
- 描述一端闭合而另一端开口的管道中的共振
- 描述两端开口的管道中的共振
干扰是海浪的标志,所有这些干扰都表现出与水浪完全相似的建设性和破坏性干扰。 实际上,证明某物 “是波浪” 的一种方法是观察干扰效应。 由于声音是一种波浪,我们预计它会产生干扰。
声波的干扰
在波浪中,我们讨论了波函数的干扰,这些函数仅在相移中有所不同。 我们发现由\(y_{1}(x, t)=A \sin (k x-\omega t+\phi)\)和的叠加产生的波函数\(y_{2}(x, t)=A \sin (k x-\omega t)\)是
\[ y(x, t)=\left[2 A \cos \left(\frac{\phi}{2}\right)\right] \sin \left(k x-\omega t+\frac{\phi}{2}\right). \nonumber \]
要使最初处于相位的两个相同波浪彼此异相,一种方法是让波浪传播不同的距离;也就是说,它们具有不同的路径长度。 声波是路径差异引起的相移的一个很好的例子。 正如我们已经讨论过的那样,声波基本上可以建模为纵波,介质分子围绕平衡位置振荡,也可以建模为压力波。
当波浪离开扬声器时,它们会像球形波一样向外移动(图\(\PageIndex{1}\))。 波浪会干扰;建设性推断是由两个波峰或两个低谷的组合产生的,如图所示。 破坏性干扰是由低谷和波峰的组合产生的。
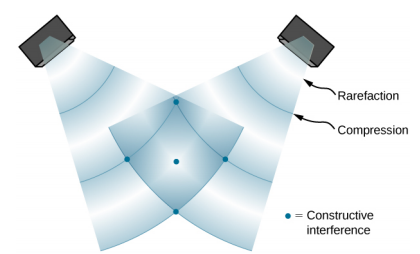
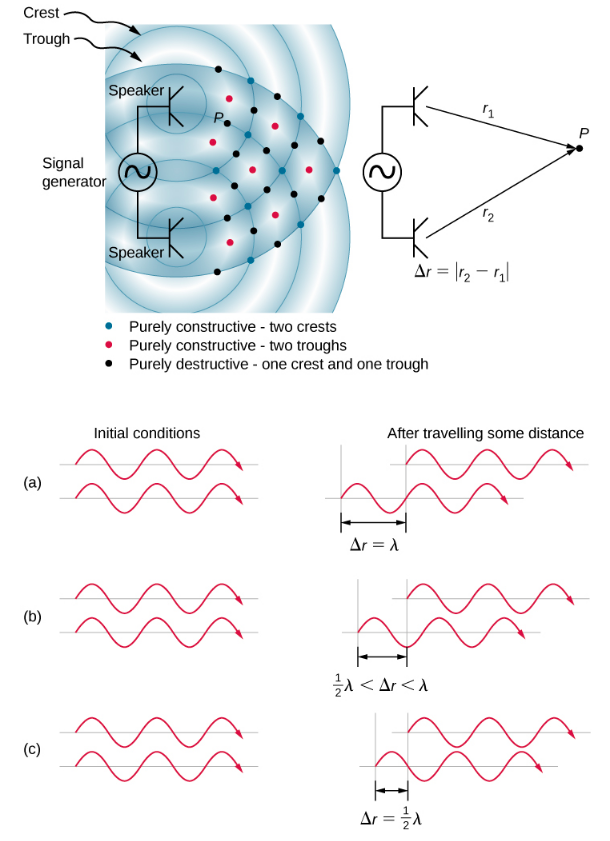
每个点的相位差是由于每个波浪所走的路径长度不同。 当路径长度的差异是波长的整数倍时,
\[ \Delta r=\left|r_{2}-r_{1}\right|=n \lambda, \text { where } n=0,1,2,3, \ldots \nonumber \]
波浪是相位的,存在建设性的干扰。 当路径长度的差异是半波长的奇数倍时,
\[ \Delta r=\left|r_{2}-r_{1}\right|=n \frac{\lambda}{2}, \text { where } n=1,3,5, \ldots \nonumber \]
波浪相位相差180°(\(\pi\)rad),结果是破坏性干扰。 这些点可以用声级强度计来定位。
两个扬声器间隔 5.00 m,由信号发生器以未知频率驱动。 拿着声级计的学生走出 6.00 m 然后向下 2.00 m,找到第一个最小强度,如下所示。 信号发生器提供的频率是多少? 假设声音的波速为 v = 343.00m/s。
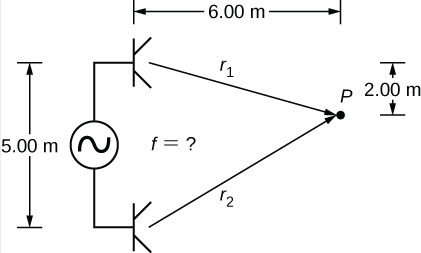
策略
波速等于\(v = \frac{\lambda}{T} = \lambda f\)。 那时频率是\(f = \frac{v}{\lambda}\)。 最小强度表示破坏性干扰,第一个这样的点出现在路径差异的地方\(\Delta r = \lambda / 2\),这可以从几何图形中找到。
解决方案
1。 找出每个扬声器到最小点的路径长度
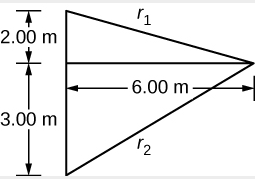
\[ r_{1}=\sqrt{(6.00 \: \mathrm{m})^{2}+(2.00 \: \mathrm{m})^{2}}=6.32 \: \mathrm{m}, r_{2}=\sqrt{(6.00 \: \mathrm{m})^{2}+(3.00 \: \mathrm{m})^{2}}=6.71 \: \mathrm{m} \nonumber \]
2。 使用路径长度的差值来查找波长。
\ begin {array} {c}
\ Delta r=\ left|r_ {2}-r_ {1}\ right|=|6.71\:\ mathrm {m} -6.32\:\ mathrm {m} |=0.39\:\ lambda=2
\ Delta r=2 (0.39\:\ mathrm {m}) =0.78\:\ mathrm {m}\ nonum
ber\ end {array}
3。 找到频率。
\[ f=\frac{v}{\lambda}=\frac{343.00 \: \mathrm{m} / \mathrm{s}}{0.78 \: \mathrm{m}}=439.74 \: \mathrm{Hz} \nonumber \]
意义
如果点 P 是最大强度的点,则路径长度将是波长的整数倍。
如果你在两个扬声器里四处走动播放音乐,为什么你没有注意到音乐非常响亮或非常柔和的地方,也就是说,有建设性和破坏性干扰的地方?
由于路径长度差异而导致的相移的概念非常重要。 你将在《干扰》和《光子与物质波》中再次使用这个概念,我们将讨论托马斯·杨在他著名的双缝实验中如何使用这种方法来提供光具有波状特性的证据。
通过破坏性干扰降低噪音
\(\PageIndex{3}\)该图显示了巧妙地使用声音干扰来消除噪音的方法。 已提议在商用飞机的整个乘客舱中更大规模地应用通过破坏性干扰进行主动降噪。 为了获得破坏性干扰,需要进行快速电子分析,然后引入第二个声音与原始声音相位180°,其最大值和最小值与传入噪声完全相反。 流体中的声波是压力波,符合帕斯卡原理;也就是说,来自两个不同来源的压力像简单数字一样相加和减去。 因此,正负表压增加的压力要小得多,从而产生较低强度的声音。 尽管只有在最简单的条件下才可能出现完全破坏性的干扰,但使用这种技术可以将噪声水平降低 30 dB 或更多。
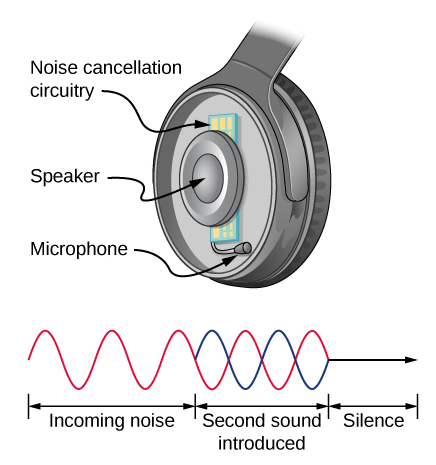
描述降噪耳机与用于阻挡外界声音的标准耳机有何不同。
我们还能在哪里观察到声音干扰? 所有声音共振,例如乐器中的共振,都是由建设性和破坏性干扰造成的。 只有共振频率会进行建设性干扰以形成驻波,而其他频率会破坏性干扰并且不存在。
一端封闭的管道中的共振
正如我们在 Waves 中所讨论的那样,驻波是由两个向相反方向移动的波浪形成的。 当两个相同的正弦波向相反的方向移动时,可以将波浪建模为
\[ y_{1}(x, t)=A \sin (k x-\omega t) \text { and } y_{2}(x, t)=A \sin (k x+\omega t) \nonumber .\]
当这两个波浪干扰时,产生的波是驻波:
\[ y_{\mathrm{R}}(x, t)=[2 A \sin (k x)] \cos (\omega t) . \nonumber \]
由于对波浪施加的边界条件,可能会产生共振。 在 Waves 中,我们展示了共振可以在具有对称边界条件的张力下在弦中产生,具体而言,两端都有一个节点。 我们将节点定义为字符串没有移动的固定点。 我们发现,对称的边界条件导致某些频率产生共振并产生驻波,而其他频率会造成破坏性干扰。 声波可以在空心管中产生共振,共振的声波的频率取决于边界条件。
假设我们有一根管子一端封闭,另一端开启。 如果我们在管子的开口端附近握住振动音叉,则入射的声波会穿过管道并从封闭的一端反射。 反射的声音与入射声波具有相同的频率和波长,但传播的方向相反。 在管道的封闭端,空气分子几乎没有振荡的自由度,因此出现了一个节点。 在开放端,分子可以自由移动,而在正确的频率下,抗阳极物会出现。 与管弦上驻波的对称边界条件不同,管子一端开口而另一端封闭的边界条件是反对称的:封闭端为节点,开口端为反向节点。
如果音叉的频率恰到好处,则管道中的气柱会产生响亮的共振,但在大多数频率下,它的振动很小。 这个观测结果只是意味着气柱只有一定的自然频率。 考虑一下会导致电子管产生共振从而产生响亮声音的最低频率。 封闭端会有一个节点,开放端会有一个反节点,如图所示\(\PageIndex{4}\)。
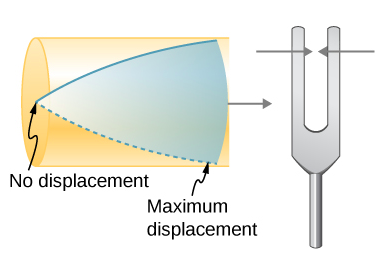
管中形成的驻波在开口端有一个抗阳极,在封闭端有一个节点。 从节点到反极点的距离是波长的四分之一,这等于管的长度;因此,\(\lambda_1 = 4L\)。 在管道封闭端或附近引入的振动也可能产生同样的共振(图\(\PageIndex{5}\))。 最好将其视为气柱的自然振动,不管它是如何产生的。
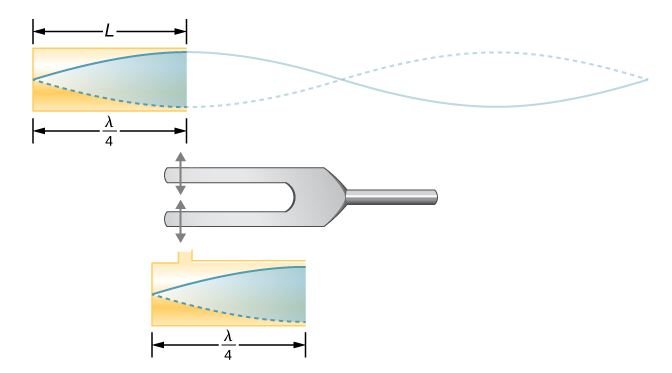
鉴于开口端可能有最大的空气位移,而在封闭端则没有排气量,因此其他较短的波长可以在管中产生共振,例如图中所示的波长\(\PageIndex{6}\)。 这里驻波有四分之三的波长在管中,或者说\(\frac{3}{4} \lambda_3 = L\),就是这样\(\lambda_3 = \frac{4}{3} L\)。 继续这个过程会发现一系列波长更短、频率更高的声音,它们在电子管中产生共鸣。 我们使用特定的术语来表示任何系统中的共振。 最低的谐振频率称为基波,而所有较高的谐振频率都称为泛音。 作为基波整数倍数的谐振频率统称为谐波。 基波是第一谐波,第二谐波是第一次谐波频率的两倍,依此类推。 在给定的场景中,其中一些谐波可能不存在。 图中\(\PageIndex{7}\)显示了一端封闭的管道中的基波和前三个泛音(或第一、第三、第五和第七谐波)。
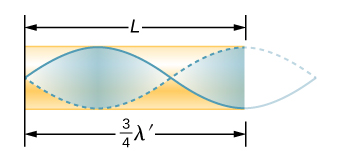
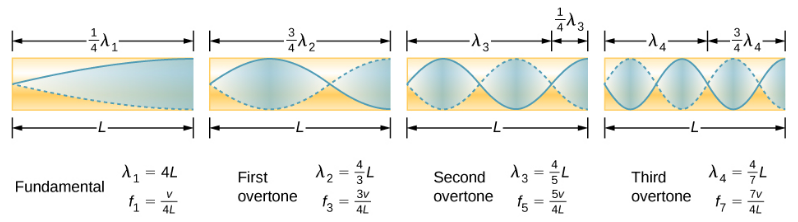
一端封闭的管的共振波长的关系为
\[\lambda_{n}=\frac{4}{n} L \quad n=1,3,5, \ldots \label{17.13} \]
现在,让我们寻找一端封闭的简单管的谐振频率模式。 基本波长\(\lambda = 4L\)和频率与波长和声速有关,如下所示
\[ v = f \lambda \nonumber .\]
在这个方程\(f\)中求解得出
\[ f=\frac{v}{\lambda}=\frac{v}{4 L}, \nonumber \]
其中 v 是空气中的声速。 同样,第一个泛音有\(\lambda = 4L/3\)(见图\(\PageIndex{7}\)),因此
\[ f_{3}=3 \frac{v}{4 L}=3 f_{1} . \nonumber \]
因为\(f_3 = 3 f_1\),我们将第一个泛音称为第三次谐波。 继续这个过程,我们看到一种可以在单个表达式中概括的模式。 一端封闭的管的谐振频率为
\[ f_{n}=n \frac{v}{4 L}, \quad n=1,3,5, \dots \label{17.14} \]
哪里\(f_1\)是基本面,\(f_3\)是第一个泛音,依此类推。 有趣的是,共振频率取决于声速,因此也取决于温度。 这种依赖性给没有暖气的旧大教堂中的器官带来了明显的问题,这也是音乐家通常在演奏管乐器之前将管乐器带到室温的原因。
管内共振,两端均开口
驻波的另一个来源是两端都开着的管子。 在这种情况下,边界条件是对称的:两端都有一个反极点。 可以用与一端封闭管道的共振非常相似的方式来分析两端开口管的共振。 两端开口的管道中的气柱在两端都有最大的空气排量(图\(\PageIndex{8}\))。 如图所示,驻波形成。
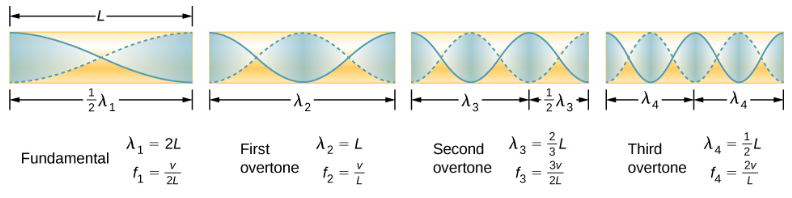
管两端开口的共振波长之间的关系为
\[ \lambda_{n}=\frac{2}{n} L, \quad n=1,2,3, \ldots \label{17.15} \]
基于这样一个事实,即两端开口的管道在两端都有最大的空气位移,并以图\(\PageIndex{8}\)为指导,我们可以看出,两端开口的管道的谐振频率为
\[ f_{n}=n \frac{v}{2 L}, \quad n=1,2,3 \dots, \label{17.16} \]
哪里\(f_1\)是基本面,\(f_2\)是第一个泛音,\(f_3\)是第二个泛音,依此类推。 请注意,两端开口的管道的基频是其一端闭合时的基频的两倍。 它还具有与一端封闭的管道不同的泛音范围。
请注意,两端开口的管道具有对称的边界条件,类似于 Waves 中讨论的固定在两端的绳子。 弦乐器的波长和频率的关系与方程\ ref {17.15} 和方程\ ref {17.16} 中给出的关系相同。 弦上波浪的速度(来自W aves)是\(v = \sqrt{\frac{F_{T}}{\mu}}\)。 琴弦周围的空气以与弦乐相同的频率振动,产生相同频率的声音。 声波以声速移动,波长可以使用来找到\(v = \lambda f\)。
怎么可能使用驻波节点和反极管来确定封闭管的长度
该视频可让您直观地看到声波。
你观察到两种你无法识别的乐器。 一个播放高音的声音,另一个播放低音的声音。 你怎么能在没有听见他们两人玩的情况下确定哪个是哪个?


