17.4: 声音强度
- Page ID
- 204219
- 定义 “强度” 一词
- 解释声强等级的概念
- 描述人耳如何翻译声音
在安静的森林里,你有时能听见一片树叶掉到地上。 但是,当路过的驾驶者打开立体声音响时,你甚至听不见车里旁边的人在说什么(图\(\PageIndex{1}\))。 我们都非常熟悉声音的响度,并且意识到响度与声源振动的能量有关。 高噪声暴露会危害听力,这就是为什么在工业环境中工作的人佩戴耳罩很重要的原因。 相关的物理量是声强,这个概念对所有声音都有效,无论它们是否在可听范围内。

以前,我们将强度定义为波浪承载的每单位面积的功率。 功率是波浪传递能量的速率。 在方程形式中,强度\(I\)为
\[I = \frac{P}{A}, \label{17.8}\]
穿过\(P\)一个区域的力量在哪里\(A\)。 的 SI 单位\(I\)为 W/m 2。 如果我们假设声波是球形的,并且热过程不会损失任何能量,那么随着距离的增加,声波的能量会散布在更大的区域上,因此强度会降低。 球体的面积为\(A = 4 \pi r^2\)。 随着波浪从\(r_1\)向蔓延\(r_2\),能量也会扩散到更大的区域:
\[\begin{align} P_{1} & = P_{2} \\[4pt] I_{1} 4 \pi r_{1}^{2} & = I_{2} 4 \pi r_{2}^{2} \\[4pt] I_{2} &= I_{1} \left(\dfrac{r_{1}}{r_{2}}\right)^{2} \ldotp \label{17.9} \end{align}\]
随着波浪从源头移出,强度会降低。 在反方关系中,例如强度,当您将距离加倍时,强度会降低到四分之一,
\[I_{2} = I_{1} \left(\dfrac{r_{1}}{r_{2}}\right)^{2} = I_{1} \left(\dfrac{r_{1}}{2r_{1}}\right)^{2} = \frac{1}{4} I_{1} \ldotp\]
通常,在考虑声波的强度时,我们将强度视为功率的时间平均值,表示为除以面积,\(⟨P⟩\)
\[I = \frac{\langle P \rangle}{A} \ldotp \label{17.10}\]
声波的强度与压力的变化平方成正比,与密度和速度成反比。 假设一块介质最初没有受到干扰,然后在时间 t 受到声波的影响,如图所示\(\PageIndex{2}\)。
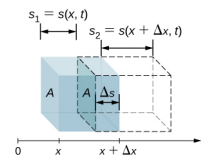
当声波穿过包裹时,包裹会移动,可能会膨胀或收缩。 如果是\(s_2 > s_1\),则体积增加而压力降低。 如果\(s_2 < s_1,\)体积减小而压力增加。 音量的变化是
\[\begin{align} \Delta V &= A \Delta s \\[4pt] &= A(s_{2} - s_{1}) \\[4pt] &= A[s(x + \Delta x,t)-s(x,t)] \ldotp \end{align}\]
音量的分数变化是音量的变化除以原始音量:
\[ \begin{align} \frac{dV}{V} &= \lim_{\Delta x \rightarrow 0} \frac{A[s(x + \Delta x,t)-s(x,t)]}{A \Delta x} \\[4pt] &= \frac{\partial s(x,t)}{\partial x} \ldotp \end{align}\]
体积的分数变化与体积模量的压力波动有关
\[\beta = − \frac{\Delta p(x, t)}{\frac{dV}{V}}.\]
回想一下,减号是必需的,因为音量与压力成反比。 (我们使用小写\(p\)的压力来区分压力和力,用表示\(P\)。) 因此,压力的变化是
\[\Delta p(x, t) = − \beta \frac{dV}{V} = − \beta \frac{\partial s(x, t)}{\partial x}.\]
如果声波是正弦波,则方程17.2所示的位移为
\[s(x, t) = s_{max} \cos(kx ∓ \omega t + \phi)\]
而且发现压力是
\[ \begin{align} \Delta p(x,t) &= - \beta \frac{dV}{V} \\[4pt] &= - \beta \frac{\partial s(x,t)}{\partial x} \\[4pt] &= \beta ks_{max} \sin (kx - \omega t + \phi) \\[4pt] &= \Delta p_{max} \sin (kx - \omega t + \phi) \ldotp \end{align}\]
声波的强度是单位面积的功率,功率是力乘以速度,
\[I = \frac{P}{A} = \frac{Fv}{A} = pv.\]
在这里,速度是介质振荡的速度,而不是声波的速度。 介质的速度是位移的时间变化率:
\[v(x,t) = \frac{\partial}{\partial y} s(x,t) = \frac{\partial}{\partial y} [s_{max} \cos (kx - \omega t + \phi)] = s_{max} \omega \sin (kx - \omega t + \phi) \ldotp\]
因此,强度变成
\[\begin{align} I & = \Delta p(x,t)\; v(x,t) \\[4pt] & = \beta ks_{max} \sin (kx - \omega t + \phi)[s_{max} \omega \sin (kx - \omega t + \phi)] \\[4pt] & = \beta k \omega s_{max}^{2} \sin^{2} (kx - \omega t + \phi) \ldotp \end{align}\]
为了找出一个位置在一个周期内的\(T = \frac{2 \pi}{\omega}\)时间平均强度\(x\),我们在该周期内进行积分,
\[I = \frac{\beta k \omega s_{max}^{2}}{2}.\]
使用\(\Delta p_{max} = \beta ks_{max}\)\(v = \sqrt{\frac{\beta}{\rho}}\)、和\(v = \frac{\omega}{k}\),我们获得
\[ \begin{align*} I &= \frac{\beta k \omega s_{max}^{2}}{2} \\[4pt] &= \frac{\beta^{2} k^{2} \omega s_{max}^{2}}{2 \beta k} \\[4pt] &= \frac{\omega (\Delta p_{max})^{2}}{2 (\rho v^{2}) k} \\[4pt] &= \frac{v (\Delta p_{max})^{2}}{2 (\rho v^{2})} \\[4pt] &= \frac{(\Delta p_{max})^{2}}{2 \rho v} \ldotp \end{align*}\]
也就是说,声波的强度与其振幅的平方有关
\[I = \frac{(\Delta p_{max})^{2}}{2 \rho v} \ldotp \label{17.11}\]
其中,\(\Delta\)p max 是压力变化或压力幅度,单位为帕斯卡 (Pa) 或 N/m 2。 行进声波产生的空气振荡元件的能量(作为动能\(\frac{1}{2} mv^2\))与其振幅平方成正比。 在此方程中,\(\rho\)是声波传播的材料的密度,单位为 kg/m 3,\(v\)是介质中的声速,单位为 m/s。压力变化与振荡的振幅成正比,因此\(I\)变化为 (\(\Delta p)^2\). 这种关系与声波是由某种振动产生的事实是一致的;声波的压力幅度越大,它产生的声音中压缩的空气就越多。
人类听觉和声音强度等级
正如本章前面所述,听觉是对声音的感知。 听觉机制涉及一些有趣的物理学。 冲击我们耳朵的声波是压力波。 耳朵是一种换能器,它以比麦克风复杂得多但类似的方式将声波转换为神经电脉冲。 该图\(\PageIndex{3}\)显示了耳朵的解剖结构。
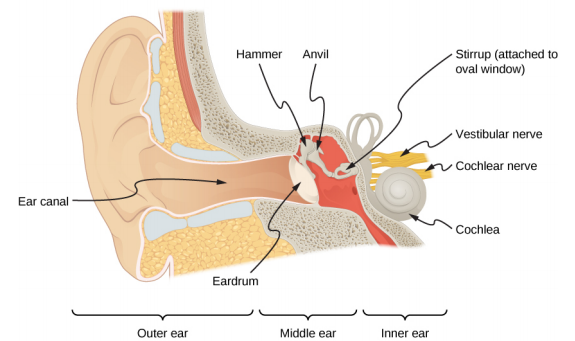
外耳或耳道将声音传送到凹陷的、受保护的耳膜。 耳道中的气柱会产生共振,是耳朵对 2000—5000-Hz 范围内声音灵敏度的部分原因。 中耳将声音转换为机械振动,并将这些振动施加到耳蜗上。
观看此视频,更详细地讨论人耳的工作原理。
人耳能听到的强度范围取决于声音的频率,但总的来说,范围相当大。 能听到的最小阈值强度为 I 0 = 10 −12 W/m 2。 疼痛是在 I 疼痛强度 = 1 W/m 2 时出现的。 由于声强范围如此之大,测量声强(以 W/m 2 为单位)非常麻烦。 出于这个原因以及其他原因,提出了声强级别的概念。
声音\(\beta\)的声强等级,以分贝为单位,强度 I 以瓦特/米平方为单位,定义为
\[\beta (dB) = \log_{10} \left(\dfrac{I}{I_{0}}\right), \label{17.12}\]
其中 I 0 = 10 −12 W/m 2 是参考强度,对应于听力正常的人在 1.00 kHz 频率下可以感知的声音阈值强度。 以 dB 为单位考虑声强度水平比以 W/m 2 为单位考虑声强度更为常见。 人耳如何感知声音可以通过强度的对数来更准确地描述,而不是直接用强度来描述。 因为 β 是根据比率定义的,所以它是一个无单位的量,它告诉你声音相对于固定标准(10 −12 W/m 2)的音量。 分贝 (dB) 单位用于表示该比率在其定义中乘以 10。 分贝所依据的铃声以电话的发明者亚历山大·格雷厄姆·贝尔的名字命名。 阈值强度为 10 −12 W/m 2 的声音的分贝级别为\(\beta\) = 0 dB,因为 log 10 1 = 0。 \(\PageIndex{2}\)该表给出了一些熟悉声音的分贝级别和以瓦特每米平方为单位的强度。 耳朵对每平方米只有万亿分之一瓦特的敏感度——当你意识到耳膜的面积只有大约 1 cm 2,因此在听觉阈值时只有 10 −16 W 落在耳朵上时,耳朵就更令人印象深刻了。 这种强度的声波中的空气分子在小于一个分子直径的距离内振动,所涉及的表压小于 10 −9 atm。
| 声强级别\(\beta\) (dB) | 强度 | 示例/效果 |
|---|---|---|
| \ (\ beta\) (dB)” >0 | 1 x 10 −12 | 1000 赫兹时的听觉阈值 |
| \ (\ beta\) (dB)” >10 | 1 x 10 −11 | 树叶的沙沙声 |
| \ (\ beta\) (dB)” >20 | 1 x 10 −10 | 在 1 米的距离低声说话 |
| \ (\ beta\) (dB)” >30 | 1 x 10 −9 | 安静的家 |
| \ (\ beta\) (dB)” >40 | 1 x 10 −8 | 普通房屋 |
| \ (\ beta\) (dB)” >50 | 1 x 10 −7 | 普通的办公室,轻柔的音乐 |
| \ (\ beta\) (dB)” >60 | 1 x 10 −6 | 普通谈话 |
| \ (\ beta\) (dB)” >70 | 1 x 10 −5 | 办公室嘈杂,交通繁忙 |
| \ (\ beta\) (dB)” >80 | 1 x 10 −4 | 响亮的广播,课堂讲座 |
| \ (\ beta\) (dB)” >90 | 1 x 10 −3 | 重型卡车内部;长时间暴露造成的损坏 [1] |
| \ (\ beta\) (dB)” >100 | 1 x 10 −2 | 工厂噪音大,警笛在 30 m 处;每天 8 小时曝光 8 小时造成损坏 |
| \ (\ beta\) (dB)” >110 | 1 x 10 −1 | 每天暴露 30 分钟造成的伤害 |
| \ (\ beta\) (dB)” >120 | 1 | 响亮的摇滚音乐会;2 米处的气动削片机;痛苦的阈值 |
| \ (\ beta\) (dB)” >140 | 1 x 10 2 | 30 米处的喷气式飞机;剧烈疼痛,几秒钟内受损 |
| \ (\ beta\) (dB)” >160 | 1 x 10 4 | 耳膜破裂 |
[1] 一些政府机构和健康相关专业协会建议,在没有听力保护的情况下,每天 8 小时的暴露量不应超过 85 dB。
通过查看表格\(\PageIndex{2}\)或使用方程式\ ref {17.12} 可以很容易地验证一个观察结果,即每个强度系数 10 对应于 10 dB。 例如,90 dB 的声音与 60 dB 的声音相比要高 30 dB,或者说强度为 10(即 10 3 倍)的三个系数。 另一个例子是,如果一个声音的强度是另一个声音的 10 7,则高出 70 dB(表\(\PageIndex{2}\))。
| \(\frac{I_{2}}{I_{1}}\) | \(\beta_{2} - \beta_{1}\) |
|---|---|
| \ (\ frac {I_ {2}} {I_ {1}}\)” style= “vertical-align: middle;” >2.0 | \ (\ beta_ {2}-\ beta_ {1}\)” style= “vertical-align: middle;” >3.0 dB |
| \ (\ frac {I_ {2}} {I_ {1}}\)” style= “vertical-align: middle;” >5.0 | \ (\ beta_ {2}-\ beta_ {1}\)” style= “vertical-align: middle;” >7.0 dB |
| \ (\ frac {I_ {2}} {I_ {1}}\)” style= “vertical-align: middle;” >10.0 | \ (\ beta_ {2}-\ beta_ {1}\)” style= “vertical-align: middle;” >10.0 dB |
| \ (\ frac {I_ {2}} {I_ {1}}\)” style= “vertical-align: middle;” >100.0 | \ (\ beta_ {2}-\ beta_ {1}\)” style= “vertical-align: middle;” >20.0 dB |
| \ (\ frac {I_ {2}} {I_ {1}}\)” style= “vertical-align: middle;” >1000.0 | \ (\ beta_ {2}-\ beta_ {1}\)” style= “vertical-align: middle;” >30.0 dB |
计算以 0°C 在空气中传播且压力振幅为 0.656 Pa 的声波的声强级别(以分贝为单位)。
策略
我们被给定了\(Δp\),所以我们可以\(I\)用方程计算
\[I = \dfrac{(\Delta p)^2}{2 \rho vw}.\]
使用\(I\),我们可以\(\beta\)直接根据其定义进行计算
\[\beta (dB) = 10 \log_{10} \left(\dfrac{I}{I_{0}}\right).\]
解决方案
- 识别已知数:声音在 0 °C 时以 331 m/s 的速度在空气中传播。大气压下空气的密度为 1.29 kg/m 3,0 °C。
- 将这些值和压力振幅输入到 I = 中\(\frac{(\Delta p)^{2}}{2 \rho v}\)。 $$I =\ frac {(\ Delta p) ^ {2}} {2\ rho v} =\ frac {(0.656\; Pa) ^ {2}} {2 (1.29\; kg/m^ {3}) (331\; m/s)} = 5.04\ times 10^ {-4}\; w/m^ {2}\ ldotp$$
- 输入 I 的值和 I 0 的已知值为\(\beta\) (dB) = 10 log 10\(\left(\dfrac{I}{I_{0}}\right)\)。 计算得出以分贝为单位的声强级别:$10\ log_ {10} (5.04\ times 10^ {8}) = (10\; dB) (8.70) = 87\; dB\ ldotp$$
意义
这种 87 dB 声音的强度是 80 dB 声音的五倍。 因此,强度为五的倍数对应于声音强度等级的差异为7 dB。 对于任何相差五倍的强度,此值均为真。
表明,如果一种声音的强度是另一种声音的两倍,则其声级高出大约 3 dB。
策略
我们得出两种强度的比值为 2 比 1,然后要求我们找出它们的声级差异(以分贝为单位)。 我们可以通过使用对数的属性来解决这个问题。
解决方案
- 识别已知数:两种强度的比率为 2 比 1,或 $$\ frac {I_ {2}} {I_ {1}} = 2.00\ ldotp$我们希望证明声级的差异约为 3 dB。 也就是说,我们想显示:$$\ beta_ {2}-\ beta_ {1} = 3\; dB\ ldotp$注意 $log_ {10} b-\ log_ {10} a =\ log_ {10}\ 左 (\ dfrac {b} {a}\ 右)\ ldotp$$
- 使用定义获得 $$\ beta_ {2}-\ beta_ {1} = 10\ log_ {10}\ 左 (\ dfrac {I_ {2}} {I_ {1}}\ 右) = 10\ log_ {10} 2.00 = (10\; dB) (0.301)\ ldotp$thus,$$\ beta_ {2}-beta_ {1} = 3.01\; dB\ ldotp$$\(\beta\)
意义
这意味着两个声音强度等级相差3.01 dB,或如广告中所说的那样约为 3 dB。 请注意,由于只给出了\(\frac{I_{2}}{I_{1}}\)比率(而不是实际强度),因此对于任何相差二倍的强度,此结果都是正确的。 例如,56.0 dB 声音的强度是 53.0 dB 声音的两倍,97.0 dB 声音的强度是 100 dB 声音的一半,依此类推。
识别 10 dB、50 dB 和 100 dB 等级的常见声音。
还使用另一种分贝刻度,称为声压级,基于压力幅度与参考压力的比率。 这种音阶特别用于声音在水中传播的应用。 处理这个音阶超出了本文的范围,因为它不常用于空气中的声音,但重要的是要注意,在引用声压等级时,可能会遇到非常不同的分贝级别。
听觉和音调
人耳具有巨大的射程和灵敏度。 它可以为我们提供大量简单的信息,例如音高、响度和方向。
对频率的感知称为音高。 通常,人类的相对音高非常好,如果两个声音的频率相差0.3%或更多,则可以区分两种声音。 例如,500.0 和 501.5 Hz 有明显的不同。 音符是大多数乐器可以产生的特定频率的声音,在西方音乐中,音符有特定的名称,例如A-sharp、C或E-flat。
对强度的感知称为响度。 在给定的频率下,可以分辨出大约 1 dB 的差异,并且很容易注意到 3 dB 的变化。 但是响度不仅仅与强度有关。 频率对声音的响度有很大的影响。 听觉范围的高频和低频极值附近的声音似乎更不响亮,因为在这些频率下,耳朵的灵敏度较低。 当小提琴演奏中音 C 时,毫无疑问是钢琴演奏相同的音符。 原因是每种乐器都会产生一组独特的频率和强度。 我们将我们对这些频率和强度组合的感知称为音质,或者更常见的是声音的音色。 音色是波浪的形状,它源于乐器中的许多反射、共振和叠加。
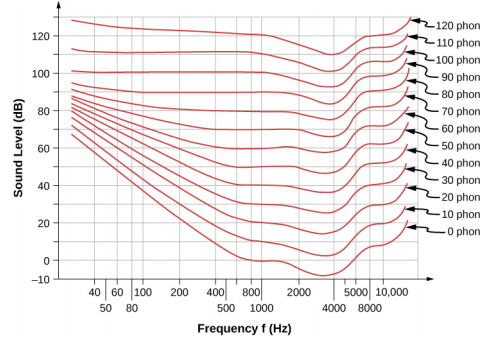
一种叫做 phon 的单位用于用数字表示响度。 电话与分贝不同,因为电话是响度感知的单位,而分贝是物理强度的单位。 该图\(\PageIndex{4}\)显示了听力正常的人的响度与强度(或强度等级)和频率的关系。 曲线是相等响度的曲线。 每条曲线都标有其在电话中的响度。 普通人认为沿着给定曲线的任何声音都同样响亮。 曲线是通过让大量人比较不同频率和声强级别下声音的响度来确定的。 在 1000 Hz 的频率下,电话在数值上被视为等于分贝。
- 强度等级为 80 dB 的 100 Hz 声音在电话中的响度是多少?
- 响度为 70 个电话的 4000-Hz 声音的强度等级(以分贝为单位)是多少?
- 在什么强度级别下,8000-Hz 的声音与 60 dB 时的 200 Hz 声音具有相同的响度?
策略
\(\PageIndex{4}\)应参考图中的图表来解决此示例。 要找到给定声音的响度,必须知道它的频率和强度级别,在方形网格上找到该点,然后在响度曲线之间进行插值以获得电话的响度。 找到该点后,就可以从垂直轴确定强度级别。
解决方案
- 识别已知数:与电话和分贝相关的图表的方形网格是强度水平与频率的关系图——两个物理量:80 dB 时的 100 Hz 位于标有 70 和 80 个电话的曲线之间。 找到响度:75 部手机。
- 识别已知数:在 70 部电话时给定值为 4000 Hz。 沿着 70 部曲线行驶,直至达到 4000 Hz。 那时,它在 70 dB 线以下,大约为 67 dB。 找到强度等级:67 dB。
- 找到 200 Hz 和 60 dB 声音的点。 找出响度:这个点略高于 50 个电话的曲线,因此它的响度为 51 个电话。 看看 51 部手机的音量为 8000 Hz: 63 dB。
意义
与从图中提取的所有信息一样\(\PageIndex{4}\),这些答案存在多个电话或几分贝的不确定性,部分原因是插值困难,但主要与等响度曲线的不确定性有关。
描述振幅与声音的响度有何关系。
在本节中,我们讨论了声音的特征和听觉方式,但是我们听到的声音是如何产生的? 有趣的声音来源是乐器和人声,我们将讨论这些来源。 但是,在我们理解乐器如何产生声音之前,我们需要先了解这些乐器背后的基本机制。 乐器所用机制背后的理论涉及干扰、叠加和驻波,我们将在下一节中讨论。


