17.3: 声速
- Page ID
- 204188
- 解释声音的波长和频率之间的关系
- 确定不同媒体中的声速
- 推导出空气中声速的方程式
- 确定给定温度下空气中的声速
像所有波浪一样,声音以一定的速度传播,具有频率和波长的特性。 在观看烟花汇演时,你可以观察到声速的直接证据(图\(\PageIndex{1}\))。 你早在听到爆炸的声音之前就看到了它的闪光,也可能感觉到压力波,这意味着声音以有限的速度传播,而且比光慢得多。

在电暴期间,也会出现光速和声速之间的差异。 闪光灯通常出现在雷声的拍手之前。 你可能听说过,如果你计算闪光灯和声音之间的秒数,就可以估计出到光源的距离。 每五秒钟转换为大约一英里。 任何波浪的速度都与其频率和波长有关
\[v = f \lambda, \label{17.3}\]
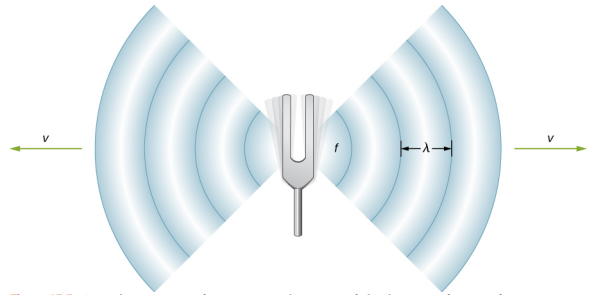
其中\(v\)是波速,\(f\)是它的频率,\(\lambda\)是它的波长。 回想一下 Wav es,波长是连续相同点之间测量的波长度。 例如,对于地表水波或串上的正弦波,可以在具有相同高度和斜率的任意两个方便的连续点之间测量波长,例如两个连续波峰或两个连续低谷之间。 同样,声波的波长是波浪中连续相同部分之间的距离,例如,连续压缩之间的距离(图\(\PageIndex{2}\))。 频率与源的频率相同,是单位时间内通过一个点的波浪数。
各种媒体中的声速
表中\(\PageIndex{1}\)显示不同媒体的声速差异很大。 介质中的声速取决于振动能量通过介质传递的速度。 因此,介质中声速的推导取决于介质和介质的状态。 一般而言,介质中机械波速度的方程取决于恢复力或弹性特性的平方根除以惯性特性,
\[v = \sqrt{\frac{\text{elastic property}}{\text{inertial property}}} \ldotp\]
\[\frac{\partial^{2} y (x,t)}{\partial x^{2}} = \frac{1}{v^{2}} \frac{\partial^{2} y (x,t)}{\partial t^{2}} \ldotp\]
回想一下 Wav es 中波浪的速度等于\(v = \sqrt{\frac{F_{T}}{\mu}}\),其中恢复力是琴弦 F T 中的张力,线性密度\(\mu\)是惯性特性。 在流体中,声速取决于体积模量和密度,
\[v = \sqrt{\frac{B}{\rho}} \ldotp \label{17.4}\]
固体中的声速取决于介质的杨氏模量和密度,
\[v = \sqrt{\frac{Y}{\rho}} \ldotp \label{17.5}\]
在理想气体中(参见《气体动力学理论》),声速方程为
\[v = \sqrt{\frac{\gamma RT_{K}}{M}}, \label{17.6}\]
其中\(\gamma\)是绝热指数,R = 8.31 j/moL • K 是气体常数,T K 是以开尔文为单位的绝对温度,M 是分子质量。 一般来说,介质越坚硬(或可压缩性越低),声音的速度就越快。 这种观察结果类似于这样一个事实,即简单谐波运动的频率与以弹簧常数 k 测量的振荡物体的刚度成正比。 媒体的密度越大,声音的速度越慢。 这种观察结果类似于这样一个事实,即简单谐波运动的频率与振荡物体的质量 m 成反比。 空气中的声速很低,因为空气很容易压缩。 由于液体和固体相对坚硬且很难压缩,因此此类介质中的声速通常比气体中的声速快。
由于声速取决于材料的密度,而密度取决于温度,因此给定介质中的温度与介质中的声速之间存在关系。 对于海平面的空气,声速由下式给出
\[v = 331\; m/s \sqrt{1 + \frac{T_{C}}{273 °C}} = 331\; m/s \sqrt{\frac{T_{K}}{273\; K}} \label{17.7}\]
其中第一个方程(表示为 T C)中的温度以摄氏度为单位,第二个方程(表示为 T K)中的温度以开尔文为单位。 气体中的声速与气体中颗粒的平均速度有关,
\[v_{rms} = \sqrt{\frac{3k_{B}T}{m}}.\]
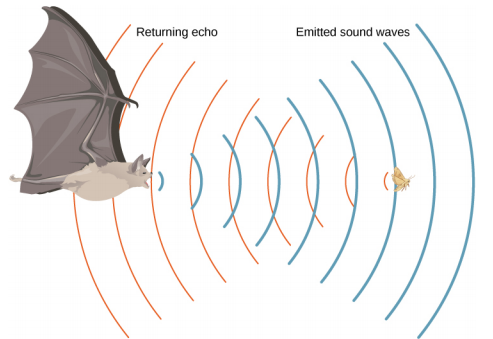
其中\(k_B\)是玻尔兹曼常数(1.38 x 10 −23 J/K),m 是气体中每个(相同)粒子的质量。 请注意,v 是指干扰(波浪)的相干传播速度,而\(v_{rms}\)描述的是粒子在随机方向上的速度。 因此,空气和其他气体中的声速应取决于温度的平方根是合理的。 尽管不可忽视,但这并不是一种强烈的依赖性。 在 0°C 时,声速为 331 m/s,而在 20.0 °C 时,声速为 343 m/s,增幅不到 4%。 该图\(\PageIndex{3}\)显示了蝙蝠如何使用声速来感知距离。
推导空中声速
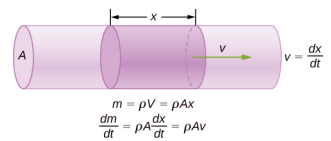
如前所述,介质中的声速取决于介质和媒体的状态。 空气中声速方程的推导始于《流体力学》中讨论的质量流速和连续性方程。 以流体流经具有横截面积的管道为\(A\)例(图\(\PageIndex{4}\))。 小体积长度的管道\(x\)中的质量等于密度乘以体积,或
\[m = \rho V = \rho Ax.\]
质量流速为
\[\frac{dm}{dt} = \frac{d}{dt} (\rho V) = \frac{d}{dt} (\rho Ax) = \rho A \frac{dx}{dt} = \rho Av \ldotp\]
流体力学的连续性方程指出,流入体积的质量流速必须等于流出体积的质量流速,
\[\rho_{in} A_{in}v_{in} = \rho_{out} A_{out}v_{out}.\]
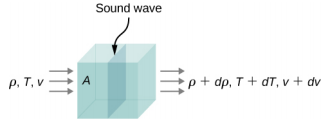
现在假设声波在空气包裹中移动。 空气包是指具有虚构边界的少量空气(图\(\PageIndex{5}\))。 流体体积一侧的密度、温度和速度以 T\(\rho\)、v 表示,另一侧为\(\rho\) + d\(\rho\)、\(T + dT\)、\(v + dv\)。
连续性方程指出,进入体积的质量流速等于离开体积的质量流量,所以
\[\rho Av = (\rho + d \rho)A(v + dv) \ldotp\]
这个方程可以简化,注意面积会抵消,并考虑到两个无穷小数的乘法大约等于零:d\(\rho\) (dv) β 0,
\[\begin{split} \rho v & = (\rho + d \rho)(v + dv) \\ & = \rho v + \rho (dv) + (d \rho)v + (d \rho)(dv) \\ 0 & = \rho (dv) + (d \rho) v \\ \rho\; dv & = -v\; d \rho \ldotp \end{split}\]
流体体积上的净力(图\(\PageIndex{6}\))等于左面和右面上的力之和:
\[\begin{split} F_{net} & = p\; dy\; dz - (p + dp)\; dy\; dz \ & = p\; dy\; dz\; - p\; dy\; dz - dp\; dy\; dz \\ & = -dp\; dy\; dz \\ ma & = -dp\; dy\; dz \ldotp \end{split}\]
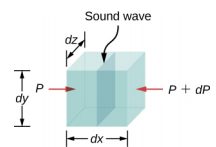
图\(\PageIndex{6}\):
加速度等于力除以质量,质量等于密度乘以体积,m =\(\rho\) V = d\(\rho\) x dy dz。 我们有
\[\begin{split} ma & = -dp\; dy\; dz \\ a & = - \frac{dp\; dy\; dz}{m} = - \frac{dp\; dy\; dz}{\rho\; dx\; dy\; dz} = - \frac{dp}{\rho\; dx} \\ \frac{dv}{dt} & = - \frac{dp}{\rho\; dx} \\ dv & = - \frac{dp}{\rho dx} dt = - \frac{dp}{\rho} \frac{1}{v} \\ \rho v\; dv & = -dp \ldotp \end{split}\]
从连续性方程\(\rho\) dv = −vd\(\rho\) 中,我们得到
\[\begin{split} \rho v\; dv & = -dp \\ (-v\; d \rho)v & = -dp \\ v & = \sqrt{\frac{dp}{d \rho}} \ldotp \end{split}\]
假设声波在空中移动。 在气体的压缩和膨胀过程中,不会向系统中添加或排出任何热量。 不向系统添加热量或从系统中去除热量的过程称为绝热系统。 《热力学第一定律》详细介绍了绝热过程,但就目前而言,只要说对于绝热过程来说,压力在哪里\(pV^{\gamma} = \text{constant}\),\(p\)就是体积,\(V\)gamma (\(\gamma\)) 是一个取决于气体的常数就足够了。 对于空气,\(\gamma\)= 1.40。 密度等于摩尔数乘以摩尔质量除以体积,因此体积等于 V =\(\frac{nM}{\rho}\)。 摩尔数和摩尔质量是恒定的,可以被常数 p\(\left(\dfrac{1}{\rho}\right)^{\gamma}\) = 常数吸收。 取两边的自然对数得出 ln p −\(\gamma\) ln\(\rho\) = 常数。 相对于密度进行微分,方程变为
\[\begin{split} \ln p - \gamma \ln \rho & = constant \\ \frac{d}{d \rho} (\ln p - \gamma \ln \rho) & = \frac{d}{d \rho} (constant) \\ \frac{1}{p} \frac{dp}{d \rho} - \frac{\gamma}{\rho} & = 0 \\ \frac{dp}{d \rho} & = \frac{\gamma p}{\rho} \ldotp \end{split}\]
如果可以将空气视为理想气体,我们可以使用理想气体定律:
\[\begin{split} pV & = nRT = \frac{m}{M} RT \\ p & = \frac{m}{V} \frac{RT}{M} = \rho \frac{RT}{M} \ldotp \end{split}\]
这里的 M 是空气的摩尔质量:
\[\frac{dp}{d \rho} = \frac{\gamma p}{\rho} = \frac{\gamma \left(\rho \frac{RT}{M}\right)}{\rho} = \frac{\gamma RT}{M} \ldotp\]
由于声速等于 v =\(\sqrt{\frac{dp}{d \rho}}\),因此速度等于
\[v = \sqrt{\frac{\gamma RT}{M}} \ldotp\]
请注意,在较高的温度下速度更快,而对于较重的气体,速度较慢。 对于空气,\(\gamma\)= 1.4,M = 0.02897 kg/mol,R = 8.31 j/mol • K。如果温度为 T C = 20 °C(T = 293 K),则声速为 v = 343 m/s。\(\sqrt{\frac{\gamma RT}{M}}\)可以简化空气中声速的方程式 v =绝对温度:
\[\begin{split} v & = \sqrt{\frac{\gamma RT}{M}} \\ & = \sqrt{\frac{\gamma RT}{M} \left(\dfrac{273\; K}{273\; K}\right)} = \sqrt{\frac{(273\; K) \gamma R}{M}} \sqrt{\frac{T}{273\; K}} \\ & \approx 331\; m/s \sqrt{\frac{T}{273\; K}} \ldotp \end{split}\]
声音最重要的特性之一是它的速度几乎与频率无关。 对于可听范围内的声音,这种独立性在露天肯定是正确的。 如果这种独立性不是真的,比如说一支游行乐队在足球场演奏的音乐,你肯定会注意到这一点。 假设高频声音传播得更快,那么你离乐队越远,来自低音乐器的声音与高音乐器的声音就越滞后。 但是所有乐器的音乐都是以与距离无关的节奏传递的,因此所有频率必须以几乎相同的速度传播。 回想一下
\[v = f \lambda \ldotp\]
在固定条件下的给定介质中,\(v\)是恒定的,因此\(f\)和之间存在关系\(\lambda\);频率越高,波长越小(图\(\PageIndex{7}\))。

计算在 30.0 °C 空气中可听范围的极限波长,即 20 和 20,000 Hz。 (假设频率值精确到两个有效数字。)
策略
要从频率中找到波长,我们可以使用\(v = f \lambda\)。
解决方案
- 识别已知数。 的值\(v\)由下式给出\[v = 331\; m/s \sqrt{\frac{T}{273\; K}} \ldotp \nonumber\]
- 将温度转换为开尔文,然后在方程中输入温度\[v = 331\; m/s \sqrt{\frac{303\; K}{273\; K}} = 348.7\; m/s \ldotp \nonumber\]
- 求解速度和波长之间的关系\(\lambda\):$$\ lambda =\ frac {v} {f}\ ldotp\ nonumber$$
- 输入速度和最小频率以给出最大波长:\[\lambda_{max} = \frac{348.7\; m/s}{20\; Hz} = 17\; m \ldotp \nonumber\]
- 输入速度和最大频率以给出最小波长:\[\lambda_{min} = \frac{348.7\; m/s}{20,000\; Hz} = 0.017\; m = 1.7\; cm \ldotp \nonumber\]
意义
因为\(f\)乘以的乘积\(\lambda\)等于常数,所以越小\(f\)是,\(\lambda\)必须越大,反之亦然。
当声音从一种媒体传播到另一种媒体时,声速可能会改变,但频率通常保持不变。 这类似于弦上波浪的频率等于振荡弦的力的频率。 如果\(v\)变化并\(f\)保持不变,则波长\(\lambda\)必须改变。 也就是说,因为\(v = f \lambda\),声音的速度越高,其在给定频率下的波长就越大。
想象一下,你观察到两枚烟花弹爆炸。 你一看见它就能听见爆炸声。 但是,在听到爆炸声之前,你会看到另一枚炮弹几毫秒。 解释为什么会这样。
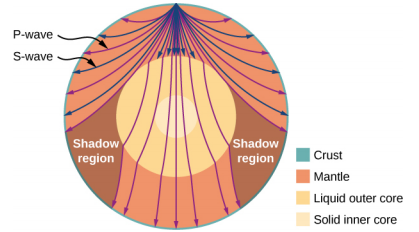
尽管流体中的声波是纵向的,但固体中的声波既是纵波又是横向波传播。 地震波本质上是地震在地壳中产生的声波,是声速如何取决于介质刚度的一个有趣例子。 地震会产生纵波和横波,它们以不同的速度传播。 花岗岩的体积模量大于其剪切模量。 出于这个原因,花岗岩地震中的纵波或压力波(P 波)的速度明显高于横向波或横波(S 波)的速度。 两种类型的地震波在硬度较低的物质(例如沉积物)中的传播速度都较慢。 P 波的速度为 4 到 7 km/s,S 波的速度从 2 到 5 km/s 不等,在更坚硬的材料中两者都更快。 当P波穿越地壳时,它们会逐渐领先于S波。 P 波和 S 波之间的时间通常用于确定到其来源(地震的震中)的距离。 由于 S 波不穿过液核,因此会产生两个阴影区域(图\(\PageIndex{8}\))。
当声波离开扬声器或远离地震震中时,它们每单位面积的功率会降低。 这就是为什么扬声器附近的声音很大,当你离开扬声器时声音变得不那么响的原因。 这也解释了为什么地震的震中可能会造成极大的破坏,而在远离震中的地区只能感受到地震。 单位面积的功率称为强度,在下一节中,我们将讨论强度如何取决于与源的距离。


