17.2: 声波
- Page ID
- 204235
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- 解释声音和听觉的区别
- 将声音描述为波浪
- 列出用于对声波进行建模的方程
- 描述与声音相关的压缩和稀有度
声音的物理现象是一种物质干扰，从其源头向外传播。 听觉是对声音的感知，就像看见是对可见光的感知一样。 在原子尺度上，声音是对原子的干扰，其有序性远远超过其热运动。 在许多情况下，声音是一种周期性波，原子经历简单的谐波运动。 因此，声波可以诱发振荡和共振效应（图\(\PageIndex{2}\)）。
这段视频显示了由扬声器发出的声波驱动的酒杯表面的波浪。 当声波的频率接近酒杯的共振频率时，酒杯上波浪的振幅和频率就会增加。 当达到共振频率时，玻璃就会破碎。
视频\(\PageIndex{1}\)：通过以共振频率播放声音，使用共振来打破酒杯。 https://www.youtube.com/watch?v=17tqXgvCN0E
扬声器通过振动圆锥体产生声波，从而引起空气分子的振动。 在图中\(\PageIndex{2}\)，扬声器以恒定的频率和振幅振动，在周围的空气分子中产生振动。 当扬声器来回振荡时，它会将能量传递到空气，主要是热能。 但是，扬声器的一小部分能量用于压缩和膨胀周围空气，从而产生稍高和较低的局部压力。 这些压缩（高压区域）和稀有区域（低压区域）作为纵向压力波向外移动，其频率与扬声器相同，它们是声波的干扰。 （空气和大多数流体中的声波是纵向的，因为流体几乎没有剪切强度。 在固体中，声波既可以是横向的，也可以是纵向的。）
该图\(\PageIndex{2a}\)显示了压缩和稀有度，还显示了表压与扬声器距离的关系图。 当扬声器向正 x 方向移动时，它会推动空气分子，使它们脱离平衡位置。 当扬声器向负 x 方向移动时，由于恢复力，空气分子会向其平衡位置移动。 空气分子以简单的谐波运动围绕其平衡位置振荡，如图所示\(\PageIndex{2b}\)。 请注意，空气中的声波是纵向的，在图中，波浪沿正 x 方向传播，分子与波浪传播的方向平行振荡。
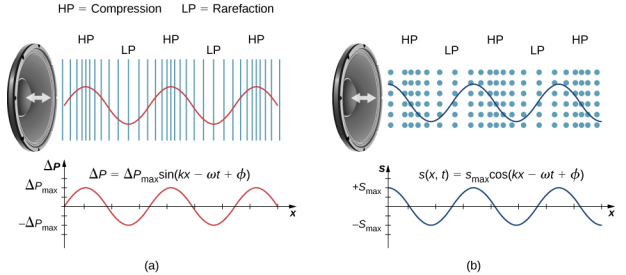
通过考虑压力与平均压力的变化，可以将声音建模为压力波，
\[\Delta P = \Delta P_{max} \sin (kx \mp \omega t + \phi) \ldotp \label{17.1}\]
该方程类似于波浪中的周期波动方程，其中\(\Delta\) P 是压力的变化，\(\Delta P_{max}\)是压力的最大变化，\(k = \frac{2 \pi}{\lambda}\)是波数，\(\omega = \frac{2 \pi}{T} = 2 \pi f\)是角频率，\(\phi\)是初始相位。 波速可以通过以下公式确定
\[v = \frac{\omega}{k} = \frac{\lambda}{T}.\]
也可以根据空气分子的位移对声波进行建模。 可以使用余弦函数对空气分子的位移进行建模：
\[s(x, t) = s_{max} \cos(kx \mp \omega t + \phi) \ldotp \label{17.2}\]
在此方程中，\(s\)是位移，\(s_{max}\)是最大位移。
图中没有显示声波的振幅，因为声波的能量分布在越来越大的区域上，因为声波的振幅随着与源的距离而减小。 如 Waves 中所述，当它离开扬声器时，强度会降低。 能量也会被物体吸收，并通过空气的粘度转化为热能。 此外，在每次压缩期间，少量热量传递到空气中；在每次稀释期间，空气中的热传递甚至更少，这些热传递将有组织的干扰减少为随机的热运动。 从压缩到稀疏的热传递是否显著取决于它们之间的距离——也就是说，取决于波长。 与所有波浪一样，波长、频率、振幅和传播速度是声音的重要特征。