16.E: Waves（练习）

概念性问题

16.1 旅行波浪

1. 举一个横波的例子和一个纵波的例子，注意每个波中干扰和波传播的相对方向。
2. 正弦横波的波长为 2.80 m。在 x 位置处的一部分弦从 y = 0.03 m 的最大位置移动到平衡位置 y = 0 需要 0.10 秒。 波浪的周期、频率和波速是多少？
3. 传播速度和机械波频率有什么区别？ 其中一个或两个都会影响波长吗？ 如果是这样，怎么办？
4. 以拉伸弹簧为例，比如紧身裤。 拉伸弹簧可以支撑纵波和横波。 你怎么能在弹簧上产生横向波浪？ 你怎么能在弹簧上产生纵波？
5. 假设在拉伸的弹簧上按住一端然后上下摇动它会产生一波浪。 波长是否取决于您上下移动手的距离？
6. 正弦横向波是在拉伸的弹簧上产生的，周期为 T。弹簧的每个部分都垂直于波浪的传播方向移动，振幅为 A 的简单谐波运动。每个部分的振荡周期与波浪相同，还是周期不同？ 如果横波的振幅翻了一番，但周期保持不变，你的答案会一样吗？
7. 电磁波，例如光，不需要介质。 你能想出一个支持这个说法的例子吗？

16.2 波浪数学

8. 如果你每秒上下摇动拉紧弹簧的末端 10 次，那么弹簧上产生的正弦波的频率和周期是多少？
9. 如果以 f 频率上下摇动拉伸弹簧的末端，则会产生沿弹簧向下传播的正弦横波。 波数取决于你摇动弹簧的频率吗？
10. 横向正弦波传播的水平拉紧线段的垂直速度是否取决于横向波的波速？
11. 在本节中，我们考虑了以恒定波速移动的波浪。 介质会加速吗？
12. 如果你在池塘里掉下卵石，你可能会注意到会产生几个同心波纹，而不仅仅是单个波纹。 你为什么这么认为？

16.3 拉伸绳上的波速

13. 如果弦中的张力增加了四倍，那么弦上波浪的波速会增加什么系数？
14. 如果海水和淡水的温度相同，声波在海水或淡水中移动得更快，声波在海水或淡水中移动得更快吗？ $$\ rho_ {w}\ 大约 1000\; kg/m^ {3}，\ rho_ {s}\ 大约 1030\; kg/m^ {3}，B_ {w} = 2.15\ times 10^ {9}\; Pa, B_ {s} = 2.34\ times 10^ {9}\; Pa$$
15. 吉他的琴弦具有不同的线性质量密度。 如果最低密度串和最高密度串处于相同的张力下，那么哪根弦会支持波速更高的波浪？
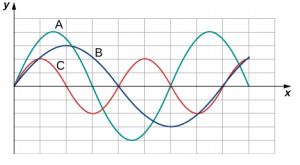
16. 下图显示了在不同时间沿着一根字符串发出的三个波浪。 琴弦中的张力保持不变。 (a) 从最小波长到最大波长对波长进行排序。 (b) 从最低频率到最高频率对波进行排序。

17. 当被风吹向振荡时，有时会听到由两根电线杆连接的电线发出嗡嗡声。 电力线上波浪的速度取决于张力。 是什么造成了电力线的张力？
18. 将两根弦拼接在一起，一根具有低质量密度，另一根具有高线性密度。 较高密度的一端与实验室柱子相连，学生拿着低质量密度串的自由端。 学生翻一下琴弦，然后向琴弦向下发送脉冲。 如果两根弦的张力相同，脉冲在两根弦中传播的波速是否相同？ 如果不是，它在低密度串还是高密度弦中传播得更快？

16.4 波浪的能量和力量

19. 以张力不足且线性质量密度恒定的弦为例。 一种由某种外部驱动力产生的角频率和振幅的正弦波。 如果驱动力的频率降低到原始频率的一半，那么波浪的时间平均功率会受到什么影响？ 如果驱动力的振幅减少一半，则时间平均功率会受到怎样的影响？ 解释你的答案。
20. 当圆形水浪离开岩石掉落的地方时，振幅会减小。 解释原因。
21. 在弦上的横向波浪中，弦的运动垂直于波浪的运动。 如果是这样，怎么可能沿着弦的长度移动能量？
22. 来自太阳的能量在白天使面向太阳的地球部分变暖。 为什么北极和南极很冷，而赤道很温暖？
23. 随着波浪离开源头，球形波的强度会降低。 如果源头波浪的强度为 I ₀，则强度在离源多远的地方会减少九倍？

16.5 波浪的干扰

24. 入射的正弦波沿着固定在墙上的绳子发出，波速为 v。波浪从弦的末端反射。 描述反射波。
25. 一根长度为 2.00 m、线性质量密度为\(\mu\) = 0.006 kg/m 的绳子连接到一根 2.00 米长、线性质量密度为\(\mu\) = 0.012 kg/m 的绳子的末端。较高密度绳的自由端固定在墙上，学生握住低密度绳的自由端，保持两根弦的张力恒定。 学生沿着琴弦向下发送脉冲。 描述两个字符串之间的接口处会发生什么。
26. 一个长而紧张的春天由两个学生举办，两端各有一个学生握住。 每个学生翻转一下末端，将一个波长的正弦波沿着相反的方向沿弹簧向下传输。 当波浪在中间相遇时，波浪是什么样子？
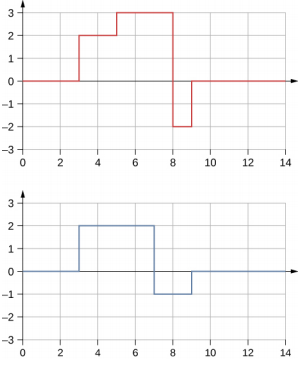
27. 除了机械波主题之外，本章讨论的许多主题都很有用。 很难想象会有尖角的机械波，但是在数字电子课上你可能会遇到这样的波形，如下所示。 这可能是来自称为模数转换器的设备的信号，在该设备中，连续的电压信号被转换为离散信号或声音的数字录音。 两个信号叠加的结果是什么？

28. 一串恒定线性质量密度的绳子由两个学生拉紧，每个学生握住一端。 琴弦中的张力是恒定的。 每个学生都通过摆动绳子将波浪沿着绳子向下发出。 (a) 波浪有可能有不同的波速吗？ (b) 波浪有可能有不同的频率吗？ (c) 波浪有可能有不同的波长吗？

16.6 驻波和共振

29. 一家卡车制造商发现发动机中的支柱过早失效。 音响工程师确定支柱以发动机的频率产生共振，并怀疑这可能是问题所在。 为了纠正这个问题，可以修改支柱的哪两个可能的特征？
30. 为什么地震发生时，体育馆和教堂的屋顶似乎比家庭住宅更容易失效？
31. 通过弄湿手指并在玻璃杯边缘摩擦酒杯，可以使酒杯产生共鸣。 为什么？
32. 空调机组有时会放在城市房屋的屋顶上。 有时，空调会在房屋的较高楼层引起不良的嗡嗡声。 为什么会发生这种情况？ 可以做些什么来减少嗡嗡声？
33. 以建模为 y (x, t) = 4.00 cm sin (3 m ⁻¹ x) cos (4 s ⁻¹ t) 的驻波为例。 x = 0.00 m 处是否有节点或反向节点？ 建模为 y (x, t) = 4.00 cm sin (3 m ⁻¹ x +\(\frac{\pi}{2}\)) cos (4 s ⁻¹ t) 的驻波怎么样？ 在 x = 0.00 m 的位置是否有节点或反向节点？

问题

16.1 旅行波浪

34. 南太平洋的风暴可以产生海浪，一直传播到12,000公里外的加利福尼亚海岸。 如果它们以 15.0 m/s 的速度行驶这个距离需要多长时间？
35. 游泳池中的波浪以 0.75 m/s 的速度传播。你把水溅到游泳池的一端，观察海浪流向另一端，反射，然后在 30.00 秒后返回。游泳池的另一端有多远？
36. 阵风在海洋上产生波长为 5.00 cm 并以 2.00 m/s 的速度传播的波纹。它们的频率是多少？
37. 一艘船每分钟在波长为 40.0 m、传播速度为 5.00 m/s 的海浪上上下摆动多少次？
38. 营地的侦察兵摇动他们刚刚穿过的索桥，观察波峰相距 8.00 米。 如果他们每秒摇动桥梁两次，波浪的传播速度是多少？
39. 如果你以 2.00 Hz 的速度挥手，而波浪以 0.800 m/s 的波速传播，那么你在游泳池中产生的波长是多少？
40. 地震以 10.0 Hz 的频率震动你，并在 12.0 秒内到达另一个 84.0 公里外的城市，其波长是多少？
41. 旅行者号航天器以光速（v = c = 3.00 x 10 ⁸ m/s）通过空白空间传输的无线电波的波长为 0.120 m。它们的频率是多少？
42. 您的耳朵能够区分每只耳朵相隔仅0.34毫秒的声音，这对于确定低频声音的来源非常有用。 (a) 假设一个低频声源放置在一个人的右边，耳朵相距约 18 厘米，产生的声音速度为 340 m/s。声音到达右耳和声音到达左耳之间的间隔有多长？ (b) 假设同一个人在水肺潜水，水肺潜水员的右边有一个低频声源。 如果水中的声速为 1500 m/s，声音到达右耳和声音到达左耳之间的间隔有多长？ (c) 这两种情况的时间间隔有什么重要意义？
43. (a) 地震仪测量地震的到达时间，精度为 0.100 秒。为了获得到地震震中的距离，地质学家比较了以不同速度传播的 S 波和 P 波的到达时间。 如果在所考虑的区域内，S 波和 P 波分别以 4.00 和 7.20 km/s 的速度传播，那么如何精确地确定到地震源的距离？ (b) 核弹地下爆炸产生的地震波可用于确定试验场的位置和发现违反试验禁令的行为。 讨论你对 (a) 的回答是否意味着对此类检测的严重限制。 （另请注意，如果S波和P波的传播速度存在不确定性，则不确定性会更大。）
44. 一名女童子军正在徒步10.00公里以获得功绩徽章。 在徒步旅行时，她看到一段距离之外的悬崖。 她想估计一下步行到悬崖所需的时间。 她知道声速约为每秒 343 米。 她大喊大叫，发现回声在大约 2.00 秒后又回来了。 如果她能在 10 分钟内徒步 1.00 公里，她要花多长时间才能到达悬崖？
45. 一家煎锅公司的质量保证工程师被要求对新系列的不粘涂层煎锅进行认证。 涂层的厚度必须为 1.00 mm。 测试厚度的一种方法是让工程师从制造的平底锅中挑选一定百分比，去掉涂层，然后使用千分尺测量厚度。 这种方法是一种破坏性测试方法。 相反，工程师决定使用非破坏性方法对每个煎锅进行测试。 使用超声波换能器产生频率为 f = 25 kHz 的声波。 声波通过涂层发送，并通过涂层和金属锅之间的界面反射，并记录时间。 涂层中超声波的波长为 0.076 m。如果涂层厚度正确（1.00 mm），应该记录多长时间？

16.2 波浪数学

46. 脉冲可以描述为在介质中移动的单波干扰。 假设一个在时间 t = 0.00 s 时由方程 y (x) =\(\frac{6.00\; m^{3}}{x^{2} + 2.00\; m^{2}}\) 以 x = 0.00 m 为中心定义的脉冲。脉冲以 v = 3.00 m/s 的速度在正 x 方向上移动。 (a) 脉冲的振幅是多少？ (b) 脉冲随位置和时间变化的方程是多少？ (c) 时间 t = 5.00 秒时脉冲的中心位置在哪里？
47. 字符串上的横向波浪使用波函数 y (x, t) = (0.20 cm) sin (2.00 m ⁻¹ x − 3.00 s ⁻¹ t +\(\frac{\pi}{16}\)) 建模。 相对于位置 x = 4.00 m 和时间 t = 10.00 s 处的平衡位置，弦的高度是多少？
48. 考虑波函数 y (x, t) = (3.00 cm) sin (0.4 m ⁻¹ x + 2.00 s ⁻¹ t +\(\frac{\pi}{10}\))。 波函数建模的波浪的周期、波长、速度和初始相移是多少？
49. 脉冲定义为 y (x, t) =\(e ^{−2.77 \left(\dfrac{2.00(x − 2.00\; m/s(t))}{5.00\; m}\right)^{2}}\)。 使用电子表格或其他计算机程序，将脉冲绘成中间 y 的高度作为位置 x 的函数。在同一张图上绘制时间 t = 0.00 s 和 t = 3.00 秒的脉冲。 时间 t = 3.00 秒时脉冲的中心位置在哪里？ 使用电子表格检查答案。
50. 波浪在时间 t = 0.00 s 时建模，波浪函数取决于位置。 方程为 y (x) = (0.30 m) sin (6.28 m ⁻¹ x)。 波浪在 0.50 秒内沿正 x 方向传播 4.00 米的距离。 为波浪写一个作为位置和时间函数的方程。
51. 波浪是使用函数 y (x, t) = (0.25 m) cos (0.30 m ⁻¹ x − 0.90 s ⁻¹ t +\(\frac{\pi}{3}\)) 建模的。 找出波浪的 (a) 振幅、(b) 波数、(c) 角频率、(d) 波速、(e) 初始相移、(f) 波长和 (g) 周期。
52. 地表海浪的振幅为 0.60 m，从海槽到海槽的距离为 8.00 m。它以 1.50 m/s 的恒定波速移动，沿正 x 方向传播。 t = 0 时，x = 0 处的水位移为零，而 vy 为正。 (a) 假设波浪可以建模为正弦波，写一个波函数来对波浪进行建模。 (b) 使用电子表格在同一张图上绘制时间 t = 0.00 s 和 t = 2.00 秒的波浪函数。 验证波浪在这 2.00 秒内移动了 3.00 m。
53. 波浪由波函数 y (x, t) = (0.30 m) sin 建模\(\Big[ \frac{2 \pi}{4.50\; m} (x − 18.00\; m/s\; t) \Big]\)。 波浪的振幅、波长、波速、周期和频率是多少？
54. 弦上的横波是用波函数 y (x, t) = (0.50 cm) sin (1.57 m ⁻¹ x − 6.28 s ⁻¹ t) 来描述的。 (a) 波浪的波速是多少？ (b) 垂直于运动方向的弦的最大速度的大小是多少？
55. 有一天，一位在海里游泳的人观察到海面波浪是周期性的，类似于正弦波。 游泳运动员估计，每波浪的波峰和波谷之间的垂直距离约为0.45米，每个波峰之间的距离约为1.8米。游泳运动员计算每两分钟有12波浪通过。 确定描述这些波浪的简单谐波函数。
56. 以波浪函数 y (x, t) = 0.3 m sin (2.00 m ^{−1 x − 628.00 s −1} t) 描述的波浪为例。 (a) 在 2.00 分钟内，观察者在固定地点经过多少波峰？ (b) 那段时间浪潮走了多远？
57. 以波浪函数 y ₁ (x, t) = 0.50 m sin\(\left(\dfrac{2 \pi}{3.00\; m}x + \dfrac{2 \pi}{4.00\; s}t \right)\) 和 y ₂ (x, t) = 0.50 m sin 定义的两个波浪为例\(\left(\dfrac{2 \pi}{6.00\; m}x − \dfrac{2 \pi}{4.00\; s}t \right)\)。 这两个浪潮有什么相似之处和不同之处？
58. 以波浪函数 y ₁ (x, t) = 0.20 m sin\(\left(\dfrac{2 \pi}{6.00\; m}x − \dfrac{2 \pi}{4.00\; s}t \right)\) 和 y ₂ (x, t) = 0.20 m cos 定义的两个波浪为例\(\left(\dfrac{2 \pi}{6.00\; m}x − \dfrac{2 \pi}{4.00\; s}t \right)\)。 这两个浪潮有什么相似之处和不同之处？
59. 弦上横向波的速度为 300.00 m/s，其波长为 0.50 m，振幅为 20.00 cm。 弦上的粒子需要多长时间才能在 5.00 km 的距离内移动？

16.3 拉伸绳上的波速

60. 横波沿着一根 500 米长的绳子发出，速度为 30.00 m/s。弦的张力为 10.00 N。弦的质量是多少？
61. 铜线的密度\(\rho\)为 = 8920 kg/m ³，半径为 1.20 mm，长度为 L。电线的张力为 10.00 N。横向波沿着电线发出。 (a) 电线的线性质量密度是多少？ (b) 波浪穿过电线的速度是多少？
62. 钢琴钢丝的线性质量密度为\(\mu\) = 4.95 x 10 ⁻³ kg/m。琴弦在多大张力下才能产生波速为 500.00 m/s 的波浪？
63. 一根线性质量密度为\(\mu\) = 0.0060 kg/m 的绳子绑在天花板上。 20 千克的重量绑在绳子的自由端上。 琴弦被弹出，向琴弦向下发送脉冲。 估计脉冲沿着弦向下移动时的速度。
64. 绳索的线性质量密度为\(\mu\) = 0.0075 kg/m，长度为三米。 电线被拔掉，脉冲需要0.20秒才能到达琴弦的末端。 琴弦的张力是多少？
65. 一根绳子长 3.00 m，质量为 5.00 g。绳子被拉紧并施加 500.00 N 的张力。 脉冲沿着字符串向下发出。 脉冲传播绳子的 3.00 m 需要多长时间？
66. 声波在 STP 处穿过氮气柱。 假设密度\(\rho\)为 = 1.25 kg/m ³，体积模量\(\beta\)为 = 1.42 x 10 ⁵ Pa，那么声波的大致速度是多少？
67. 在 T = 28°C 的温度下，声音在空气中传播的大概速度是多少？
68. 横波穿过张力等于 7.00 N 的绳子，速度为 20.00 m/s。波速为 25.00 m/s 需要多大的张力？
69. 两根绳子连接在两极之间，间隔距离为 2.00 m，两极的张力相同，即 600.00 N。String 1 的线性密度为\(\mu_{1}\) = 0.0025 kg/m，弦 2 的线性质量密度为\(\mu_{2}\) = 0.0035 kg/m。横波脉冲同时产生在琴弦的两端。 脉冲经过多长时间才相互传递？

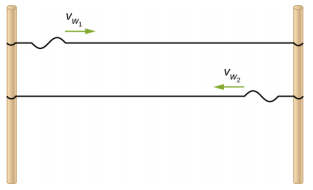
70. 两根绳子连接在两极之间，间隔距离为 2.00 米，如上图所示，两根弦的线性密度为\(\mu_{1}\) = 0.0025 kg/m，弦 1 中的张力为 600.00 N，弦 2 中的张力为 700.00 N 横波脉冲同时产生琴弦的两端。 脉冲经过多长时间才相互传递？
71. 音符 E ₄ 是在钢琴上演奏的，频率为 f = 393.88。 如果这根钢琴弦的线性质量密度为\(\mu\) = 0.012 kg/m，而琴弦的张力为 1000.00 N，那么琴弦上波浪的速度和波长的波长是多少？
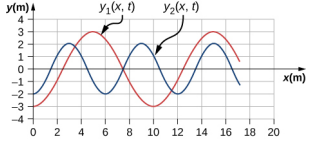
72. 两个横向的波浪穿过一根拉紧的绳子。 每个波浪的速度为 v = 30.00 m/s。下图显示了时间 t = 0.00 s 时垂直位置与水平位置的函数。(a) 每个波浪的波长是多少？ (b) 每个波浪的频率是多少？ (c) 每根弦的最大垂直速度是多少？

73. 正弦波沿着一条拉紧的水平弦向下传播，线性质量密度为 μ = 0.060 kg/m。 波浪的最大垂直速度为 vy max = 0.30 cm/s。波浪使用波动方程 y (x, t) = A sin (6.00 m ⁻¹ x − 24.00 s ⁻¹ t) 建模。 (a) 波浪的振幅是多少？ (b) 琴弦中的张力是多少？
74. 弦上横波的速度为 v = 60.00 m/s，弦中的张力为 F _T = 100.00 N。 要将波速提高到 v = 120.00 m/s，张力必须是多少？

16.4 波浪的能量和力量

75. 一根长度为 5 m、质量为 90 g 的绳子在 100 N 的张力下保持一根波浪沿着弦向下移动，其模型为 y (x, t) = 0.01 m\(\sin\) (15.7 m ⁻¹ x − 1170.12 s ⁻¹)。 一个波长的功率是多少？
76. 强度为 1.50 x 10 ^{2 W/m 2} 的超声波由医疗成像设备的矩形头部产生，尺寸为 3.00 cm x 5.00 cm。 它的功率输出是多少？
77. 立体声装置的低频扬声器的表面积为 A = 0.05 m ²，产生 1 W 的声功率。 (a) 扬声器的强度是多少？ (b) 如果扬声器在各个方向上均匀投射声音，则强度 0.1 W/m ² 与扬声器之间的距离是多少？
78. 要将波浪的强度增加50倍，振幅应该增加哪个系数？
79. 一种称为日照计的设备用于测量阳光的强度。 它的面积为 100 cm ²，记录为 6.50 W。以 W/m ² 为单位的强度是多少？
80. 来自太阳的能量以 1400 W/m ² 的强度到达地球大气层的顶部。 1.80 x 10 ⁹ J 需要多长时间才能到达 1.00 m ² 的区域？
81. 假设你有一个设备可以从海洋破碎机中提取能量，其能量与其强度成正比。 如果设备在断路器高达 1.20 米的那一天产生 10.0 kW 的功率，那么当断路器高 0.600 m 时，它会产生多少功率？
82. 光伏阵列（太阳能电池）在收集太阳能并将其转化为电能方面的效率为10.0％。 如果一天的日光平均强度为 70.00 W/m ²，那么您的阵列应在哪个区域以 100 W 的速率收集能量？ (b) 如果阵列必须在两年的运营时间内收回成本，平均每天运行10.0小时，其最高成本是多少？ 假设它以每千瓦时9.00美分的速度赚钱。
83. 接收纯净音调的麦克风为示波器供电，在其屏幕上产生波浪。 如果声强最初为 2.00 x 10 ⁻⁵ W/m ²，但在振幅增加 30.0% 之前一直调高，那么新的强度是多少？
84. 质量为 0.30 kg 的弦的长度为 4.00 m。如果弦中的张力为 50.00 N，并且在琴弦上产生振幅为 2.00 cm 的正弦波，则平均功率为 100.00 W 的频率必须是多少？
85. 上图显示了引发正弦行波的弦上某个点（\(\mu\)= 0.05 kg/m）的功率与时间的关系。 波浪使用波动方程 y (x, t) = A sin (20.93 m ⁻¹ x −\(\omega\) t) 建模。 波浪的频率和振幅是多少？
86. 一根绳子处于张力下 F _T1。 能量由弦上的波浪以 P ₁ 的速率通过频率为 f ₁ 的波传输。 如果张力加倍，新能源传输速率 P ₂ 与 P ₁ 的比率是多少？
87. 250-Hz 音叉被敲击，在距离音源一米的距离处，音源的强度为 I1。 (a) 距离源头 4.00 m 处的强度是多少？ (b) 音叉离音叉有多远，强度是音源强度的十分之一？ 88。 扬声器的额定电压为 P = 120.00 V，电流为 I = 10.00 A。电力消耗为 P = IV。 为了测试扬声器，向扬声器施加正弦波信号。 假设声波以球形波的形式移动，并且施加在扬声器上的所有能量都转换为声能，那么距离扬声器有多远的强度等于 3.82 W/m ²？
88. 池塘上波纹的能量与振幅的平方成正比。 如果波纹在距离源头6.00米处的振幅为0.1厘米，则距离源2.00米处的振幅是多少？

16.5 波浪的干扰

90. 假设两个沿着字符串传播的正弦波，建模为 y ₁ (x, t) = 0.3 m sin（4 m ⁻¹ x + 3 s ⁻¹ t）和 y ₂ (x, t) = 0.6 m sin（8 m ⁻¹ x − 6 s ⁻¹ t）。 在时间 t = 0.2 s 时 x = 0.5 m 位置的两个波浪的干扰所形成的合成波的高度是多少？
91. 假设两个沿着字符串传播的正弦波，建模为 y ₁ (x, t) = 0.3 m sin（4 m ⁻¹ x + 3 s ⁻¹ t +\(\frac{\pi}{3}\)）和 y ₂ (x, t) = 0.6 m sin（8 m ⁻¹ x − 6 s ⁻¹ t）。 在时间 t = 3.0 s 时 x = 1.0 m 位置的两个波浪的干扰所形成的合成波的高度是多少？
92. 假设两个沿着字符串传播的正弦波，建模为 y ₁ (x, t) = 0.3 m sin（4 m ⁻¹ x − 3 s ⁻¹ t）和 y ₂ (x, t) = 0.3 m sin（4 m ⁻¹ x + 3 s ⁻¹ t）。 生成的波浪的波函数是什么？ [提示：使用 trig 身份 sin (u ± v) = sin u cos v ± cos u sin v]
93. 两个正弦波沿相同的方向穿过介质，两者的振幅均为 3.00 cm，波长为 5.20 m，周期为 6.52 秒，但其中一个的相移为一个角度\(\phi\)。 如果合成波的振幅为 5.00 cm，相移是多少？ [提示：使用触发身份 sin u + sin v = 2 sin\(\left(\dfrac{u + v}{2}\right)\) cos\(\left(\dfrac{u − v}{2}\right)\)]
94. 两个正弦波在正 x 方向上穿过介质，两者的振幅均为 6.00 cm，波长为 4.3 m，周期为 6.00 s，但其中一个的相移角度\(\phi\) = 0.50 rad。 在 t = 3.15 秒、位置 x = 0.45 m 时，合成波浪的高度是多少？
95. 两个正弦波在正 x 方向上穿过介质，两者的振幅均为 7.00 cm，波数为 k = 3.00 m−1，角频率为\(\omega\) = 2.50 s ⁻¹，周期为 6.00 秒，但其中一个的相移角度\(\phi\) =\(\frac{\pi}{12}\) rad。 在 t = 2.00 s、位置 x = 0.53 m 时，合成波浪的高度是多少？
96. 假设两个波浪 y ₁ (x, t) 和 y ₂ (x, t) 除了在同一介质中传播的相移外，它们是相同的。 (a) 如果生成的波浪的振幅是单个波浪振幅的1.75倍，以弧度为单位的相移是多少？ (b) 以度为单位的相移是多少？ (c) 相移占单个波长的百分比是多少？
97. 除了相移外，两个完全相同的正弦波沿着相同的方向传播。 合成波浪的波动方程为 y _R (x, t) = 0.70 m sin (3.00 m ⁻¹ x − 6.28 s ⁻¹ t +\(\frac{\pi}{16}\) rad)。 单个波浪的角频率、波数、振幅和相移是多少？
98. 除了相移外，两个完全相同的正弦波沿着相同的方向传播。 合成波浪的波动方程为 y _R (x, t) = 0.35 cm sin (6.28 m ⁻¹ x − 1.57 s ⁻¹ t +\(\frac{\pi}{4}\))。 单个波浪的周期、波长、振幅和相移是多少？
99. 考虑两个波函数，y ₁ (x, t) = 4.00 m sin（\(\pi\)m ⁻¹ x −\(\pi\) s ⁻¹ t）和 y ₂ (x, t) = 4.00 m sin（\(\pi\)m ⁻¹ x −\(\pi\) s ⁻¹ t +\(\frac{\pi}{3}\)）。 (a) 使用电子表格，绘制两个波函数和两个波函数叠加产生的波浪作为 t = 0.00 s 时位置函数 (0.00 ≤ x ≤ 6.00 m)。(b) 两个原始波浪的波长和振幅是多少？ (c) 生成的波长的波长和振幅是多少？
100. 考虑两个波函数，y ₂ (x, t) = 2.00 m sin（\(\frac{\pi}{2}\)m ⁻¹ x −\(\frac{\pi}{3}\) s ⁻¹ t）和 y ₂ (x, t) = 2.00 m sin（\(\frac{\pi}{2}\)m ⁻¹ x −\(\frac{\pi}{3}\) s ⁻¹ t +\(\frac{\pi}{6}\)）。 (a) 验证 y _R = 2A cos\(\left(\dfrac{\phi}{2}\right)\) sin (kx −\(\omega\) t +\(\frac{\phi}{2}\)) 是两个波浪叠加产生的波浪的解。 _{为 x、y 1、y 2、y 1 + y 2 和 y R = 2A cos\(\left(\dfrac{\phi}{2}\right)\) sin (kx −\(\omega\) t +\(\frac{\phi}{2}\)) 创建一列。} 将四个波浪绘制为位置的函数，其中 x 的范围为 0 到 12 m。
101. 考虑两个仅有相移差异的波函数，y ₁ (x, t) = A cos (kx −\(\omega\) t) 和 y ₂ (x, t) = A cos (kx −\(\omega\) t +\(\phi\))。 使用三角恒等式 cos u + cos v = 2 c\(\left(\dfrac{u − v}{2}\right)\) os cos\(\left(\dfrac{u + v}{2}\right)\) 和 cos (−\(\theta\)\(\theta\)) = cos () 来找出两个波浪叠加产生的波浪方程。 生成的波浪函数会让你感到惊讶吗？

16.6 驻波和共振

102. 在拉伸到 4 米的 Slinky® 上传播的波浪需要 2.4 秒才能在 Slinky 的长度上传播然后再次返回。 (a) 波浪的速度是多少？ (b) 使用相同的 Slinky 拉伸到相同长度，生成由三个反向节点和四个节点组成的驻波。 Slinky 必须以什么频率振荡？
103. 一根 2 米长的绳子在两个支撑之间拉伸，其张力产生的波速等于 v _w = 50.00 m/s。在弦上产生共鸣的前三种模式的波长和频率是多少？
104. 以如下所示的实验设置为例。 弦式振动器和滑轮之间的弦长为 L = 1.00 m。弦的线性密度为\(\mu\) = 0.006 kg/m。弦式振动器可以以任何频率振荡。 悬挂质量为 2.00 千克。 (a) n = 6 模式的波长和频率是多少？ (b) 琴弦振荡琴弦周围的空气。 如果声音的速度为 v _{s = 343.00 m/s}，声音的波长是多少？

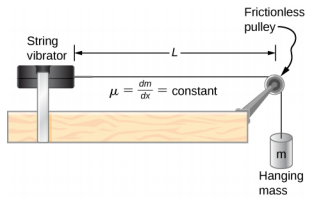
105. 线性密度\(\mu\)为 = 0.2 kg/m 的电缆悬挂在电线杆上。 电缆中的张力为 500.00 N。两极之间的距离为 20 米。 风吹过线路，引起电缆产生共鸣。 生成的驻波图案在两极之间有 4.5 个波长。 当前温度 T = 20 °C 时的声速为 343.00 m/s。嗡嗡声的频率和波长是多少？
106. 假设一根长度为 L 的杆，安装在支架的中心。 杆安装在支架上的位置必须存在节点，如下所示。 绘制杆被驱动到共振状态时的前两个法线模式。 标记驱动棒产生共振所需的波长和频率。

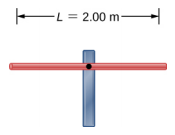
107. 考虑两个波函数 y (x, t) = 0.30 cm sin (3 m ⁻¹ x − 4 s ⁻¹ t) 和 y (x, t) = 0.30 cm sin (3 m ⁻¹ x + 4 s ⁻¹ t)。 为生成的驻波写一个波函数。
108. 一条 2.40 米的电线的质量为 7.50 g，张力为 160 N。电线的两端都牢固地固定并处于振荡状态。 (a) 电线上波浪的速度是多少？ 弦由产生波长等于 1.20 m 的驻波的频率驱动成共振。(b) 驱动琴弦产生共振的频率是多少？
109. 线性质量密度为 0.0062 kg/m、长度为 3.00 m 的弦设置为 n = 100 的共振模式。 弦中的张力为 20.00 N。波浪的波长和频率是多少？
110. 线性质量密度为 0.0075 kg/m、长度为 6.00 m 的琴弦通过以 100.00 Hz 的频率驱动，将其设置为 n = 4 的共振模式。 琴弦中的张力是多少？
111. 两个具有相同波长和振幅的正弦波沿着一根弦向相反的方向传播，产生驻波。 弦的线性质量密度为\(\mu\) = 0.075 kg/m，弦中的张力为 F _T = 5.00 N。完全破坏性干扰实例之间的时间间隔为\(\Delta\) t = 0.13 s。波浪的波长是多少？
112. 固定在两端的绳子长 5.00 m，重量为 0.15 kg。 如果琴弦为 90 N，则为张力。琴弦正在振动，以弦的基频产生驻波。 (a) 弦上波浪的速度是多少？ (b) 产生的驻波的波长是多少？ (c) 驻波周期是多少？
113. 字符串在两端都是固定的。 琴弦的质量为 0.0090 kg，长度为 3.00 m。琴弦的张力为 200.00 N。琴弦由变频源驱动，在弦上产生驻波。 找出驻波前四种模式的波长和频率。
114. 弦上两种连续驻波模式的频率为258.36 Hz和301.42 Hz。 下一个高于 100.00 Hz 的频率会产生驻波的频率是多少？
115. 一根绳子固定在两端，支撑间隔 3.50 米，线性质量密度为\(\mu\) = 0.005 kg/m。弦的张力为 90.00 N。弦上产生驻波，有六个节点和五个反向节点。 驻波的波速、波长、频率和周期是多少？
116. 正弦波沿着固定在两端的1.5米长的弦线发出。 波浪朝相反的方向反射回来。 波浪的振幅为 4.00 厘米。 波浪的传播速度为 175 m/s。产生弦的 n = 6 共振模式。 为生成的驻波写一个方程。

其他问题

117. 医学界使用的超声波设备使用频率高于人类听觉范围的声波。 如果超声波机器产生的声音频率为 f = 30 kHz，那么骨骼中超声波的波长是多少，如果骨骼中的声速为 v = 3000 m/s？
118. 下图显示的是对时间 t = 0.00 s 和 t = 2.00 s 时的波浪进行建模的波函数图。虚线是时间 t = 0.00 s 时的波函数，实线是时间 t = 2.00 s 时的函数。估计波浪的振幅、波长、速度和周期。

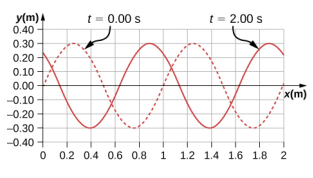
119. 空气中的光速约为 v = 3.00 x 10 ⁸ m/s，玻璃中的光速为 v = 2.00 x 10 ⁸ m/s。波长为\(\lambda\) = 633.00 nm 的红色激光照射玻璃的入射光，一些红光被传输到玻璃。 空气和玻璃的光线频率是相同的。 (a) 光的频率是多少？ (b) 玻璃中光的波长是多少？
120. 一家广播电台以 101.7 MHz 的频率广播无线电波。 无线电波在真空中以大约光速在空中移动。 无线电波的波长是多少？
121. 日光浴者站在大海深处，观察到每分钟有六个周期性地表波峰经过。 波峰相距 16.00 米。 波浪的波长、频率、周期和速度是多少？
122. 音叉振动产生频率为 512 Hz 的声音。 如果空气温度为 20.00 °C，则空气中声音的速度为 v = 343.00 m/s。声音的波长是多少？
123. 摩托艇以 v _b = 15.00 m/s 的速度穿越湖泊。船每隔 0.50 秒上下反弹一次，因为它沿着与波浪相同的方向行驶。 当它朝与波浪方向相反的方向移动时，它每隔 0.30 秒上下反弹一次。 波浪的速度和波长是多少？
124. 使用线性波动方程显示使用波函数 y (x, t) = 0.20 m sin (3.00 m ^{−1 x + 6.00 s −1} t) 建模的波速为 v = 2.00 m/s。波浪的波长和速度是多少？
125. 假设波函数 y ₁ (x, t) = A sin (kx −\(\omega\) t) 和 y ₂ (x, t) = A sin (kx −\(\omega\) t +\(\phi\)) with\(\phi \neq \frac{\pi}{2}\)，显示 y ₁ (x, t) + y ₂ (x, t) 是波速为 v = 的线性波动方程的解\(\frac{\omega}{k}\)。
126. 字符串上的横向波浪使用波函数 y (x, t) = 0.10 m sin（0.15 m ⁻¹ x + 1.50 s ⁻¹ t + 0.20）建模。 (a) 找出波速。 (b) 找出在时间 t = 5.00 s 时以 x = 0.40 m 为中心的一小段弦在 y 方向上的位置、垂直于波浪运动的速度和垂直于波浪运动的加速度。
127. 正弦波沿着一条拉紧的水平弦向下移动，线性质量密度为\(\mu\) = 0.060 kg/m。波浪的最大垂直加速度的大小为 ay max = 0.90 cm/s ²，波浪的振幅为 0.40 m。弦的张力为 F _T = 600.00 N。 波浪向负 x 方向移动。 写一个方程来模拟波浪。
128. 弦上的横波（\(\mu\)= 0.0030 kg/m）用方程式 y (x, t) = 0.30 m sin 来描述\(\left(\dfrac{2 \pi}{4.00\; m}(x − 16.00\; m/s\; t)\right)\)。 拉紧绳子的张力是多少？
129. 水平弦上的横波（\(\mu\)= 0.0060 kg/m）用方程式 y (x, t) = 0.30 m sin 来描述\(\left(\dfrac{2 \pi}{4.00\; m(x − v_{w}t)}\right)\)。 琴弦的张力为 300.00 N。波速、波数和角频率是多少？
130. 学生拿着一台便宜的声波测距仪并使用测距仪来寻找到墙壁的距离。 声波测距仪发出声波。 声波从墙上反射出来并返回测距仪。 往返需要 0.012 秒。测距仪经过校准，可在室温 T = 20 °C 下使用，但房间内的温度实际上是 T = 23 °C。假设计时机制完美，学生预计校准会导致多少百分比的误差？
131. 弦上的波浪由弦振动器驱动，振荡频率为 100.00 Hz，振幅为 1.00 cm。 弦振动器的工作电压为 12.00 V，电流为 0.20 A。弦振动器消耗的功率为 P = IV。 假设弦振动器在将电能转换为与弦振动相关的能量方面效率为90％。 琴弦长 3.00 m，张力为 60.00 N。琴弦的线性质量密度是多少？
132. 弦上的行波由波动方程 y (x, t) = 3.00 cm sin (8.00 m ⁻¹ x + 100.00 s ⁻¹ t) 建模。 琴弦的张力为 50.00 N，线性质量密度为\(\mu\) = 0.008 kg/m。琴弦上波浪传递的平均功率是多少？
133. 弦上的横波波长为 5.0 m，周期为 0.02 秒，振幅为 1.5 cm。 波浪传递的平均功率为 5.00 W。琴弦中的张力是多少？
134. (a) 用于烧掉癌组织的激光束的强度是多少，当癌组织被吸收 90.0% 时，在 4.00 秒内将 500 焦耳的能量注入直径为 2.00 mm 的圆点？ (b) 讨论这种强度与阳光的平均强度（大约）相比如何，以及激光束进入你的眼睛会产生的影响。 请注意，你的答案如何取决于曝光的持续时间。
135. 考虑两个周期波函数，y ₁ (x, t) = A sin (kx −\(\omega\) t) 和 y ₂ (x, t) = A sin (kx −\(\omega\) t +\(\phi\))。 (a) 波函数叠加产生的波浪的振幅为多少 2A？\(\phi\) (b) 波函数叠加产生的波浪的振幅为零的值是多少？\(\phi\)
136. 考虑两个周期波函数，y ₁ (x, t) = A sin (kx −\(\omega\) t) 和 y ₂ (x, t) = A cos (kx −\(\omega\) t +\(\phi\))。 (a) 波函数叠加产生的波浪的振幅为多少 2A？\(\phi\) (b) 波函数叠加产生的波浪的振幅为零的值是多少？\(\phi\)
137. 尺寸为10.00米乘0.10米乘0.10米乘0.10米的水槽部分充满了水。 小振幅地表水浪是由桨在简单的谐波运动中振荡而从水槽的两端产生的。 水浪的高度使用两个正弦波动方程建模，y ₁ (x, t) = 0.3 m sin（4 m ⁻¹ x − 3 s ⁻¹ t）和 y ₂ (x, t) = 0.3 m cos（4 m ⁻¹ x + 3 s ⁻¹ t −\(\frac{\pi}{2}\)）。 在波浪相互到达之后和到达低谷尽头之前，生成的波浪的波函数是什么（即，假设低谷中只有两个波浪而忽略反射）？ 使用电子表格查看结果。 [提示：使用 trig 身份 sin (u± v) = sin u cos v ± cos u sin v and cos (u± v) = cos u cos v sin u sin v]
138. 地震仪记录了相隔 20.00 秒的地震产生的 S 波和 P 波。 如果他们_{以 v S = 4.00 km/s} 和 v _P = 7.50 km/s 的恒定波速行驶相同的路径，那么地震的震中有多远？
139. 考虑下面显示的内容。 20.00 千克的质量位于倾斜度为 45° 的无摩擦坡道上。 线性质量密度为\(\mu\) = 0.025 kg/m 的绳子连接在 20.00-kg 的质量上。 绳子穿过质量可以忽略不计的无摩擦滑轮，并附着在悬挂物（m）上。 系统处于静态平衡状态。 波浪在琴弦上产生并沿着坡道向上移动。 (a) 悬挂物体的重量 (m) 是多少？ (b) 波浪以什么波速向上移动？

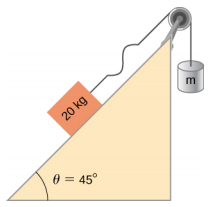
140. 考虑三个波函数 y (x, t) = 3.00 cm sin (2 m ⁻¹ x − 3 s ⁻¹ t)、y (x, t) = 3.00 cm sin (6 m ⁻¹ x + 3 s ⁻¹ t) 和 y (x, t) = 3.00 cm sin (2 m ^{−1 x −} 4 s ⁻¹ t) 的叠加。 在时间 t = 10.0 s 时 x = 3.00 m 位置生成的波浪的高度是多少？
141. 绳子的质量为 150 g，长度为 3.4 m。绳子的一端固定在实验室支架上，另一端连接到弹簧常数为 k _s = 100 N/m 的弹簧上。弹簧的自由端连接到另一根实验杆上。 琴弦中的张力由弹簧维持。 实验室两根杆之间有一段距离，弹簧延伸距离为 2.00 cm。 琴弦被弹出，脉冲沿着琴弦传播。 脉冲的传播速度是多少？
142. 驻波是在张力为 70.0 N 的弦上由两个相同但朝相反方向移动的正弦横波产生的。 字符串固定在 x = 0.00 m 和 x = 10.00 m 处。节点出现在 x = 0.00 m、2.00 m、4.00 m、6.00 m、8.00 m 和 10.00 m 处。驻波的振幅为 3.00 cm。 反极点需要0.10秒才能完成一次振荡。 (a) 产生驻波的两个正弦波的波函数是什么？ (b) 垂直于横波运动方向的弦在反向节点处的最大速度和加速度是多少？
143. 长度为 4 m 的绳子在恒定张力下保持不变。 琴弦的线性质量密度为\(\mu\) = 0.006 kg/m。弦的两个谐振频率为 400 Hz 和 480 Hz。 两个频率之间没有共振频率。 (a) 两种共振模式的波长是多少？ (b) 琴弦中的张力是多少？

挑战问题

144. 铜线的半径为 200\(\mu\) m，长度为 5.0 m。线材的张力为 3000 N，线材的拉伸量很小。 电线被拔掉，脉冲沿着电线向下移动。 脉冲的传播速度是多少？ （假设温度没有变化：（\(\rho\)= 8.96 g/cm ³，Y = 1.1 x 10 ¹¹ N/m）。
145. 沿 x 轴移动的脉冲可以建模为波函数 y (x, t) = 4.00 m\(e^{− \left(\dfrac{x + (2.00\; m/s)t}{1.00\; m}\right)^{2}}\)。 (a) 脉冲的方向和传播速度是多少？ (b) 波浪在3.00秒内移动了多远？ (c) 在时间 t = 0.00 s 和 t = 3.00 s 时使用电子表格绘制脉冲图，以验证 (b) 部分中的答案。
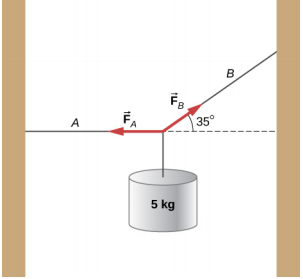
146. 线性质量密度为\(\mu\) = 0.0085 kg/m 的绳子固定在两端。 绳子上悬挂着一个 5.0 千克的重物，如下所示。 如果沿着A段发送脉冲，则A部分的波速和B部分的波速是多少？

147. 考虑两个波函数 y ₁ (x, t) = A sin (kx −\(\omega\) t) 和 y ₂ (x, t) = A sin (kx +\(\omega\) t +\(\phi\))。 两个波浪的干扰产生的波函数是什么？ [提示：sin (\(\alpha \pm \beta\)) = sin\(\alpha\) cos\(\beta\) ± cos\(\alpha\) sin\(\beta\) an\(\phi = \frac{\phi}{2} + \frac{\phi}{2}\) d)。
148. 模拟驻波的波函数以 yR (x, t) = 6.00 cm sin (3.00 m ⁻¹ x + 1.20 rad) cos (6.00 s ⁻¹ t + 1.20 rad) 给出。 哪两个波函数会干扰此波函数的形成？ 在 t = 1.00 s 处绘制两个波函数以及两个波函数之和的总和以验证您的答案。
149. 考虑两个波函数 y ₁ (x, t) = A sin (kx −\(\omega\) t) 和 y ₂ (x, t) = A sin (kx +\(\omega\) t +\(\phi\))。 当你添加这两个函数时，生成的波形是 y _R = 2A sin (kx +\(\frac{\phi}{2}\)) cos (\ omega t +\ frac {\ phi} {2}\)）。 考虑一下 A = 0.03 m ⁻¹、k = 1.26 m ⁻¹、\(\omega = \pi\) s ⁻¹ 和\(\phi = \frac{\pi}{10}\)。 (a) 驻波函数的前三个节点从零开始沿正 x 方向移动，在哪里？ (b) 使用电子表格，在时间 t = 1.00 s 绘制两个波函数和生成的函数以验证您的答案。