16.7: 驻波和共振

Last updated
Save as PDF

Page ID: 204257

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

描述驻波并解释它们是如何产生的
描述弦上驻波的模式
举例说明绳子上的波浪之外的驻波

在本章中，我们一直在研究行波或将能量从一个地方传输到另一个地方的波浪。在某些条件下，波浪可以在特定区域来回反弹，实际上变为静止状态。这些被称为驻波。

另一个相关的效应称为共振。在《振荡》中，我们将共振定义为一种现象，在这种现象中，小振幅驱动力可以产生大振幅运动。想想一个孩子在秋千上，可以将其建模为物理摆锤。母体相对较小的振幅推动会产生较大的振幅摆动。有时候这种共振是好的，例如，在用弦乐器制作音乐时。在其他时候，影响可能是毁灭性的，例如地震期间建筑物倒塌。就驻波而言，振幅相对较大的驻波是由较小的振幅分量波的叠加产生的。

驻波

有时波浪似乎没有移动；相反，它们只是在原地振动。例如，你可以在冰箱里看到一杯牛奶表面不动的波浪。来自冰箱马达的振动会在牛奶上产生波浪，波浪上下摆动，但似乎没有在表面移动。该图$\PageIndex{1}$显示了你可以在家尝试的实验。拿一碗牛奶放在普通的箱式风扇上。来自风扇的振动会在牛奶中产生圆形驻波。由于灯的反射，照片中可以看到波浪。这些波浪是由两个或两个以上的行波叠加形成的，如图$\PageIndex{2}$所示，两个相同波浪朝相反方向移动。海浪相互穿过，随着它们的流过，它们的干扰会增加。如果这两个波的振幅和波长相同，则它们会在构造干扰和破坏性干扰之间交替出现。由此产生的波浪看起来像站在原地的波浪，因此被称为驻波。

照片显示了坐在箱式风扇上的一碗牛奶表面出现波浪。 — 图$\PageIndex{1}$：坐在箱式风扇上的一碗牛奶的表面形成驻波。来自风扇的振动会导致牛奶表面振荡。由于灯光的反射，波浪是可见的。

图中显示了两个相同正弦波和一个合成波的 8 个时间快照，间隔为 1 x 8 T。在 t=0t 和 t = half T 时，两个正弦波同相，合成波的振幅是两个单独波浪的两倍。在 t = 1 x 4 T 和 t = 3 x 4 T 时，两个正弦波的相位相反，不存在合成波。 — 图$\PageIndex{2}$：两个正弦波的时间快照。红色波浪在 −x 方向移动，蓝波在 +x 方向移动。生成的波浪以黑色显示。考虑一下在 x = 0 m、3 m、6 m、9 m、12 m、15 m 处产生的波浪，注意无论时间如何，在这些点生成的波浪始终等于零。这些点被称为定点（节点）。每个节点之间都有一个反向节点，介质振荡的振幅等于单个波浪的振幅之和。

假设两个朝相反方向移动的相同波浪。第一波的波函数为 y ₁ (x, t) = A sin (kx −$\omega$ t)，第二波的波函数为 y ₂ (x, t) = A sin (kx +$\omega$ t)。波浪会干扰并形成合成的波浪

\[\begin{split} y(x,t) & = y_{1} (x,t) + y_{2} (x,t), \\ & = A \sin (kx - \omega t) + A \sin (kx + \omega t) \ldotp \end{split}\]

这可以使用三角恒等式来简化

\[\sin (\alpha \pm \beta) = \sin \alpha \cos \beta \pm \cos \alpha \sin \beta,\]

其中$\alpha$ = kx 和$\beta$ =$\omega$ t，给我们

\[y(x,t) = A[\sin (kx) \cos (\omega t) - \cos (kx) \sin (\omega t) + \sin (kx) \cos (\omega t) - \cos (kx) \sin (\omega t)],\]

这简化为

\[y(x,t) = 2A \sin (kx) \cos (\omega t) \ldotp \label{16.14}\]

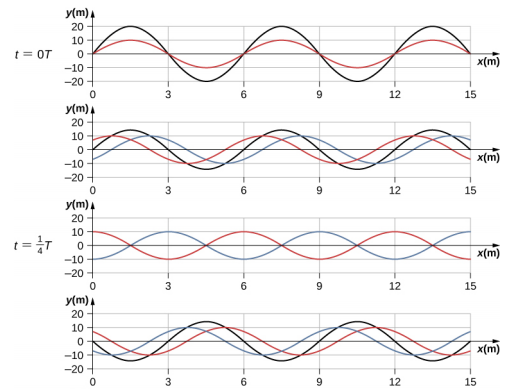
请注意，合成波是仅作为位置函数的正弦波乘以仅作为时间函数的余弦函数。 y (x, t) 作为 x 在不同时间内的函数的图形如图所示$\PageIndex{6}$。红色波浪向负 x 方向移动，蓝波沿正 x 方向移动，黑色波浪是两个波浪的总和。当红波和蓝浪相互穿过时，它们进出建设性干扰和破坏性干扰。

最初，在时间 t = 0 时，两个波浪是相位的，结果是波浪的振幅是单个波浪的两倍。波浪在 t = 时也处于同相状态$\frac{T}{2}$。实际上，波浪以半个周期的任意整数倍数同相：

t = n$\frac{T}{2}$ 其中 n = 0、1、2、3... （同期）。

在其他时候，两个波浪相位相差180°（$\pi$弧度），生成的波浪等于零。这发生在

t =$\frac{1}{4}$ T、$\frac{3}{4}$ T、$\frac{5}{4}$ T、...、$\frac{n}{4}$ T 其中 n = 1、3、5... （异相）。

请注意，无论相位关系如何，合成波的某些 x 位置始终为零。这些位置被称为节点。节点出现在哪里？考虑两个波浪之和的解

\[y(x,t) = 2A \sin (kx) \cos (\omega t) \ldotp\]

找到正弦函数等于零的位置可提供节点的位置。

\[\begin{split} \sin (kx) & = 0 \\ kx & = 0, \pi, 2 \pi, 3 \pi, \ldots \\ \frac{2 \pi}{\lambda} x & = 0, \pi, 2 \pi, 3 \pi, \ldots \\ x & = 0, \frac{\lambda}{2}, \lambda, \frac{3 \lambda}{2}, \ldots = n \frac{\lambda}{2} \quad n = 0, 1, 2, 3, \ldots \end{split}\]

还有一些位置 y 在 y = ±A 之间振荡。这些位置是反极点。我们可以通过考虑 x 的哪些值导致 sin (kx) = ±1 来找到它们。

\[\begin{split} \sin (kx) & = \pm 1 \\ kx & = \frac{\pi}{2}, \frac{3 \pi}{2}, \frac{5 \pi}{2}, \ldots \\ \frac{2 \pi}{\lambda} x & = \frac{\pi}{2}, \frac{3 \pi}{2}, \frac{5 \pi}{2}, \ldots \\ x & = \frac{\lambda}{4}, \frac{3 \lambda}{4}, \frac{5 \lambda}{4}, \ldots = n \frac{\lambda}{4} \quad n = 1, 3, 5, \ldots \end{split}\]

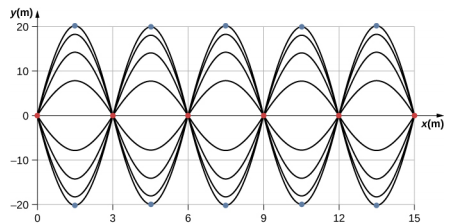
结果是驻波，如图所示$\PageIndex{3}$，其中显示了两个相同波浪向相反方向移动的生成的波浪的快照。生成的波浪似乎是正弦波，节点为半波长的整数倍数。由于余弦项 cos ($\omega$t) 在 ±1 之间振荡，反向节点在 y = ±2A 之间振荡。

由此产生的波浪似乎处于静止状态，在 x 方向上没有明显的移动，尽管它由一个向正向移动的波函数组成，而第二个波浪在负 x 方向移动。该图$\PageIndex{3}$显示了由此产生的波浪的各种快照。节点用红点标记，而对抗节点用蓝点标记。

图中显示了两个振幅变化的正弦波，相位完全相反。标有红点的节点沿着 x 轴 x = 0 m、3 m、6 m、9 m 等处。标有蓝点的抗体位于每波浪的峰值和低谷处。它们位于 x = 1.5 m、4.5 m、7.5 m 等处。 — 图$\PageIndex{3}$：当两个相同的波浪朝相反的方向移动时，生成的波浪是驻波。节点以半波长的整数倍数出现。 Antinodes 以四分之一波长的奇数倍数出现，它们在 y = ±A 之间振荡。节点用红点标记，对抗节点用蓝点标记。

驻波的一个常见例子是弦乐器产生的波浪。弹出琴弦时，脉冲会沿着相反的方向沿着绳子传播。弦的末端是固定的，因此节点出现在弦的末端——系统的边界条件，调节弦中的谐振频率。弦乐器产生的共振可以在物理实验室中使用图中所示的设备进行建模$\PageIndex{4}$。

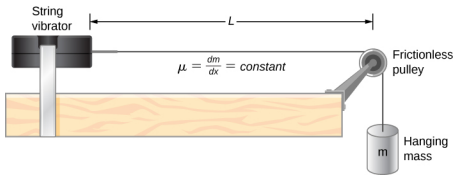
图左侧显示了弦式振动器。右边附有一根绳子。它越过滑轮然后沿着桌子的侧面向下移动。悬挂物 m 悬挂在上面。滑轮无摩擦。滑轮和弦振动器之间的距离为 L。它被标记为 mu 等于 delta m x delta x 等于常数。 — 图$\PageIndex{4}$：用于在绳子上创建驻波的实验室设置。字符串的两端都有一个节点，线性密度恒定。固定边界条件之间的长度为 L。悬挂质量提供弦中的张力，弦上波浪的速度与张力的平方根除以线性质量密度成正比。

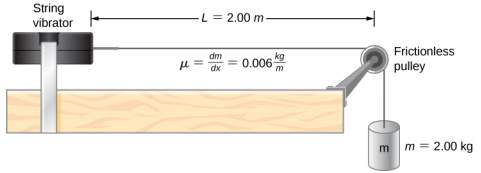
实验室设置显示了一根连接在弦振动器上的绳子，它以可调节的频率振动琴弦 f。琴弦的另一端穿过无摩擦的滑轮并绑在悬挂的物体上。绳子中的张力大小等于悬挂物体的重量。弦具有恒定的线性密度（每长度质量）$\mu$，波浪沿着弦向下移动的速度等于$v = \sqrt{\frac{F_{T}}{\mu}} = \sqrt{\frac{mg}{\mu}}$方程16.7。对称的边界条件（两端各有一个节点）决定了可能激发驻波的频率。从零频率开始，然后慢慢增加频率，第一个模式 n = 1 出现，如图所示$\PageIndex{5}$。第一种模式，也称为基模或第一谐波，显示一半的波长已经形成，因此波长等于节点之间长度的两倍$\lambda_{1}$ = 2L。 驱动此模式的基频或第一谐波频率是

\[f_{1} = \frac{v}{\lambda_{1}} = \frac{v}{2L},\]

其中，波速为 v =$\sqrt{\frac{F_{T}}{\mu}}$。保持张力恒定并增加频率会导致二次谐波或 n = 2 模式。此模式为全波长$\lambda_{2}$ = L，频率是基频的两倍：

\[f_{2} = \frac{v}{\lambda_{2}} = \frac{v}{L} = 2f_{1} \ldotp\]

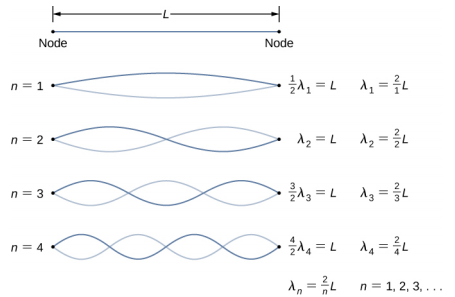
显示了长度为 L 的字符串的四位数字。每个都有两个波浪。第一个有 1 个节点。它被标记为 half lambda 1 = L，lambda 1 = 2 乘 1 倍 L。第二个数字有 2 个节点。它被标记为 lambda 2 = L，lambda 2 = 2 乘 2 倍 L。第三个数字有三个节点。它被标记为 3 乘 2 倍 lambda 3 = L，lambda 3 = 2 乘 3 倍 L。第四个数字有 4 个节点。它被标记为 4 乘 2 倍 lambda 4 = L，lambda 4 = 2 x 4 倍 L 底部有一个派生公式，lambda n 等于 2 乘 n 倍 L 表示 n = 1、2、3 等等。 — 图$\PageIndex{5}$：在一串长度上产生的驻波$L$。字符串的两端都有一个节点。节点是限制激发驻波的可能频率的边界条件。（请注意，为了可视化，振荡的振幅一直保持不变。琴弦上可能出现的驻波模式被称为普通模式。在实验室进行此实验将导致振幅随着频率的增加而降低。）

接下来的两种模式，即第三和第四次谐波，波长为$\lambda_{3} = \frac{2}{3}$ L 和$\lambda_{4} = \frac{2}{4}$ L，由 f ₃ = 3f _{1 和 f _{4$\frac{3v}{2L}$}$\frac{4v}{2L}$ = 4f ₁} 的频率驱动。所有高于频率 f1 的频率都称为泛音。波长和频率的方程可以概括为：

\[\lambda_{n} = \frac{2}{n} L \quad n = 1, 2, 3, 4, 5 \ldots \label{16.15}\]

\[f_{n} = n \frac{v}{2L} = nf_{1} \quad n = 1, 2, 3, 4, 5 \ldots \label{16.16}\]

字符串可能出现的驻波模式被称为正常模式，其频率称为正常频率，其频率如图$\PageIndex{5}$所示。总之，产生普通模式的第一个频率称为基频（或第一谐波）。任何高于基频的频率都是泛音。字符串 n = 2 正常模式的第二个频率是第一个泛音（或二次谐波）。 n = 3 普通模式的频率是第二个泛音（或三次谐波），依此类推。

方程\ ref {16.15} 和方程\ ref {16.16} 所示的解适用于两端均为节点边界条件的字符串。当任一侧的边界条件相同时，则称系统具有对称的边界条件。方程\ ref {16.15} 和方程\ ref {16.16} 适用于任何对称边界条件，即两端的节点或两端的反节点。

示例$\PageIndex{1}$: Standing Waves on a String

假设一根 L = 2.00 m 的弦连接到可调频率的弦振动器上，如图所示$\PageIndex{6}$。振动器产生的波浪沿着弦向下移动，并被滑轮上的固定边界条件反射。绳子的线性质量密度为$\mu$ = 0.006 kg/m，通过质量可以忽略不计的无摩擦滑轮，张力由 2.00 千克的悬挂质量提供。 (a) 弦上波浪的速度是多少？ (b) 绘制可以在弦上产生的驻波的前三种法线模式的草图，并用波长标记每种模式。 (c) 列出弦振动器必须调整到的频率，才能产生驻波的前三种正常模式。

图左侧显示了弦式振动器。右边附有一根绳子。它越过滑轮然后沿着桌子的侧面向下移动。悬挂物 m = 2 kg 悬挂在上面。滑轮无摩擦。滑轮和弦振动器之间的距离为 L = 2 m。它被标记为 mu 等于 delta m x delta x 等于 0.006 kg per m。 — 图$\PageIndex{6}$：连接在可调频率弦振动器上的绳子。

策略

使用 v = 可以找到波浪的速度$\sqrt{\frac{F_{T}}{\mu}}$。张力由悬挂物料的重量提供。
驻波将取决于边界条件。两端必须有一个节点。第一种模式将是波浪的一半。第二个可以通过添加半波长来找到。这是在边界处生成节点的最短长度。例如，增加四分之一的波长将导致边界处出现反向节点，这不是一种满足边界条件的模式。如图所示$\PageIndex{7}$。
由于波速速度是波长乘以频率，因此频率等于波速除以波长。

图 a 显示了两端都附有一根绳子。弦上的两个波浪在两端形成一个节点，在中心形成另一个节点。这被标记为可能的模式。图 b 显示了两端都附有一根绳子。弦上的两个波浪在弦的一端形成一个节点，在另一端形成一个反向节点。这被标记为不可能的模式。 — 图$\PageIndex{7}$-(a) 该图表示字符串的第二种模式，该模式满足字符串两端节点的边界条件。 (b) 这个数字不可能是字符串的正常模式，因为它不满足边界条件。一端有节点，另一端有反节点。

解决方案

从弦上波浪的速度开始。张力等于悬挂物体的重量。给出了悬挂物体的线性质量密度和质量：$$v =\ sqrt {\ frac {F_ {T}} {\ mu}} =\ sqrt {\ frac {mg} {\ frac {(2\; kg)} {0.006\; kg/m}} = 57.15\; m/s\ ldotp$$
第一种两端都有一个节点的普通模式是半波长。接下来的两种模式是通过添加一半的波长来找到的。

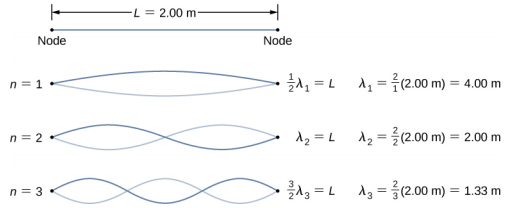
图中显示了长度为 L=2 m 的字符串中的三位数字。每个都有两个波浪。第一个有 1 个节点。它被标记为半 lambda 1 = L，lambda 1 = 2 x 1 乘以 2 m = 4 m。第二个图有 2 个节点。它被标记为 lambda 2 = L，lambda 2 = 2 乘 2 倍 2 m = 2 m。第三个图有三个节点。它被标记为 3 乘 2 倍 lambda 3 = L，lambda 3 = 2 x 3 倍 2 m = 1.33 m。

前三种模式的频率是使用 f = 得出的$\frac{v_{w}}{\lambda}$。 $$\ begin {split} f_ {1} & =\ frac {v_ {w}} {\ lambda_ {1}} =\ frac {57.15\; m/s} {4.00\; m} = 14.29\; Hz\\ f_ {2}} {\ lambda_ {2}} =\ frac {57.15; m/s} {2.00\; m} = 28.58\; Hz\\ f_ {3} & =\ frac {v_ {w}} {\ lambda_ {3}} =\ frac {57.15\; m/s} {1.333\; m} = 42.87\; Hz\ end {split} $$

意义

本例中的三种站立模式是通过保持弦中的张力并调整驱动频率而产生的。保持弦中的张力恒定会产生恒定的速度。通过保持频率恒定并调整弦中波浪的速度（通过改变悬挂质量），也可以产生同样的模式。

模拟

访问此仿真系统，玩由耦合质量弹簧振荡器组成的一维或二维系统。改变质量数量，设定初始条件，然后观察系统的演变。查看任意运动的普通模式频谱。参见 1-D 系统中的纵向或横向模式。

练习$\PageIndex{1}$

在弦上产生的波浪模式的波长和频率的方程式：

\[\begin{split} \lambda_{n} & = \frac{2}{n} L \quad n = 1, 2, 3, 4, 5 \ldots and \\ f_{n} & = n \frac{v}{2L} = nf_{1} \quad n = 1, 2, 3, 4, 5 \ldots \end{split}\]

是通过考虑字符串上的波浪得出的，其中两端都有节点的对称边界条件。这些模式是由两个具有相同特征的正弦波产生的，唯一的不同是它们朝相反的方向移动，局限于两端都需要节点的区域 L。如果存在对称的边界条件，两端都有反向点，同样的方程会起作用吗？对于两端都可以自由振荡的媒介来说，普通模式会是什么样子？如果你无法想象这样的介质，现在不用担心，只要考虑长度为 L 的区域中的两个正弦波函数，两端都有反向节点。

上一篇《检查你的理解》中显示的自由边界条件似乎很难可视化。怎么会有一个两端都能自由振荡的系统？图中显示了连接$\PageIndex{8}$在两个支架（以蓝色显示）上的金属棒（以红色显示）的两种可能配置。在 (a) 部分中，杆的两端受支撑，两端都有固定的边界条件。只要有适当的频率，棒就可以被驱动到共振，波长等于棒的长度，两端都有节点。在 (b) 部分中，杆支撑在距离杆两端长度四分之一的位置上，并且两端都有自由边界条件。只要有合适的频率，这根棒也可以被驱动成共振，波长等于棒的长度，但两端都有抗阳极。如果您在可视化此图中的波长时遇到问题，请记住，可以在任何两个最近的相同点之间测量波长，并考虑图$\PageIndex{9}$。

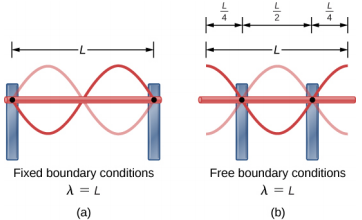
相反地，在极点支撑棒的部位形成节点，在杆的两端形成反向节点。 — 图$\PageIndex{8}$：(a) 一根长度为 L（红色）的金属棒，两端由两个支撑（蓝色）支撑。当以适当的频率驱动时，棒可以产生与棒长相等的波长共振，两端各有一个节点。 (b) 长度为L（红色）的同一根金属杆由两个支撑（蓝色）支撑，其位置为杆两端长度的四分之一。当以适当的频率驱动时，棒可以产生与棒长相等的波长共振，两端都有一个抗阳极。

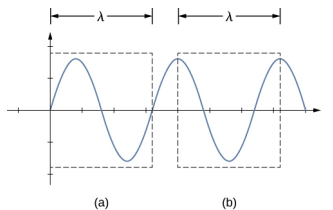
图中显示了正弦波。两个标有 a 和 b 的盒子分别标记波浪的一个波长。方框 a 测量 x 轴上两个最近的点之间的波长，波浪开始获得正值。方框 b 测量两个相邻波峰之间的波长。 — 图$\PageIndex{9}$：可以在最近的两个重复点之间测量波长。在绳子上的波浪上，这意味着相同的高度和斜率。 (a) 波长是在两个最近的点之间测量的，其中高度为零，斜率为最大且为正。 (b) 波长是在两个相同点之间测量的，其中高度为最大且斜率为零。

请注意，对驻波的研究可能会变得非常复杂。在图 16.32 (a) 中，显示了驻波的 n = 2 模式，它产生的波长等于 L。在这种配置中，如果驻波等于 2L，n = 1 模式也是可能的。是否有可能为第 (b) 部分所示的配置获得 n = 1 模式？答案是否定的。在此配置中，除了边界条件外，还设置了其他条件。由于杆安装在距离两侧四分之一长度的点上，因此那里必须存在一个节点，这限制了可能产生的驻波模式。我们将其留作练习，供读者考虑是否有可能使用其他驻波模式。应该注意的是，当系统以不引起系统共振的频率驱动时，仍可能发生振动，但振动的振幅将远小于共振时的振幅。

机械工程领域使用复杂机械系统的振动部件产生的声音来解决系统问题。假设汽车中的某个部件以汽车发动机的频率产生共振，从而在汽车中造成不必要的振动。这可能会导致引擎过早失效。工程师使用麦克风录制发动机产生的声音，然后使用一种名为傅里叶分析的技术来查找振幅较大的声音的频率，然后查看汽车的零件清单，找到能在该频率下产生共振的部件。解决方案可能很简单，例如改变所用材料的成分或改变相关零件的长度。

在物理世界中，驻波中还有许多其他共振的例子。管道中的空气，例如长笛等乐器中的空气，可以被迫产生共振并产生愉悦的声音，正如我们在《声音》中讨论的那样。

在其他时候，共振可能会导致严重的问题。仔细观察地震可以为共振、驻波以及建设性和破坏性干扰的适当条件提供证据。建筑物可能会振动几秒钟，其驱动频率与建筑物的自然振动频率相匹配，从而产生共振，导致一座建筑物倒塌，而相邻建筑物不倒塌。通常，一定高度的建筑物会被摧毁，而其他较高的建筑物则完好无损。建筑物高度符合为该特定高度设置驻波的条件。屋顶的跨度也很重要。人们常常看到，当个人住宅遭受的破坏要少得多时，体育馆、超市和教堂就会遭受破坏。仅在边缘支撑的表面积较大的屋顶在地震频率下会产生共振，导致屋顶倒塌。当地震波沿着地球表面传播并从更密集的岩石上反射出来时，某些位置会发生建设性干扰。通常，距离震中较近的区域不会受到损坏，而距离更远的区域则受到损坏。

示例\(\PageIndex{1}\): Standing Waves on a String

解决方案

模拟

练习\(\PageIndex{1}\)