Skip to main content
Global

16.6: 波浪的干扰

  1. Last updated
  2. Save as PDF
  • Page ID
    204256

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    学习目标
    • 解释机械波是如何在介质边界上反射和传输的
    • 定义 “干扰” 和 “叠加” 这两个术语
    • 找出两个相同的正弦波的合成波，这两个波的区别仅在于相移

    到目前为止，我们一直在研究通过介质持续传播的机械波，但是我们还没有讨论过当波浪遇到介质边界时会发生什么，或者当波浪遇到通过同一介质传播的另一波时会发生什么。 波浪确实与介质的边界相互作用，并且波浪的全部或部分可以被反射。 例如，当你站在距离坚硬的悬崖面有一段距离并大喊大叫时，你可以听见声波作为回声从刚性表面反射出来。 波浪还可以与在同一介质中传播的其他波浪相互作用。 如果你把两块石头扔进一个彼此相距一定距离的池塘里，这两块石头产生的圆形波纹在石头进入水中的位置传播出来时似乎会相互穿过。 这种现象被称为干扰。 在本节中，我们将研究遇到介质边界的波浪或在同一介质中传播的另一种波浪会发生什么。 我们将看到它们的行为与粒子和刚体的行为大不相同。 后来，当我们研究现代物理学时，我们会发现，只有在原子的尺度上，我们才能看到波浪和粒子特性的相似之处。

    反射和传输

    当波浪通过介质传播时，它会在遇到介质边界时反射。 到达边界前的波浪被称为入射波。 遇到边界后的波浪被称为反射波。 波浪在介质边界的反射方式取决于边界条件；如果介质的边界固定到位或可以自由移动，波浪的反应会有所不同（图\(\PageIndex{1}\)）。 当边界处的介质固定到位因此无法移动时，即存在固定边界条件。 当边界处的介质可以自由移动时，存在自由边界条件。

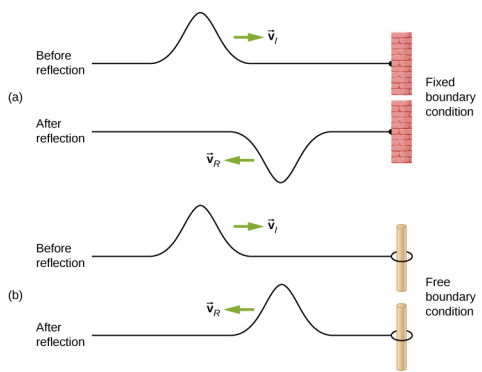
    图 a 在右侧显示了两幅附着在刚性支撑上的绳子。 顶部字符串在反射之前被标记。 在字符串顶部形成的脉冲以 velocity v 下标 i 向右传播。底部字符串在反射后被标记。 在弦底部形成的脉冲以速度 v 下标 R 向左传播。图 b 显示了两幅附着在穿过右边极点的环上的绳子。 顶部字符串在反射之前被标记。 在字符串顶部形成的脉冲以 velocity v 下标 i 向右传播。底部字符串在反射后被标记。 在字符串顶部形成的脉冲以速度 v 下标 R 向左传播
    图\(\PageIndex{1}\)：(a) 字符串的一端是固定的，因此它无法移动。 在弦上传播的波浪遇到这种固定边界条件，相对于入射波反射相位180°（\(\pi\)rad）。 (b) 绳子的一端绑在无摩擦实验室杆上的质量可以忽略不计的实心环上，环可以在那里自由移动。 在弦上传播的波浪遇到这种自由边界条件，相对于波浪以相位 0°（0 rad）反射。

    \(\PageIndex{1a}\)该图显示了固定边界条件。 在这里，绳子的一端固定在墙上，因此绳子的末端固定在适当的位置，边界处的媒介（绳子）无法移动。 当波浪被反射时，反射路径的振幅与入射波的振幅完全相同，但反射\(180^o \pi\)波相对于入射波的反射异相。 相变可以用牛顿第三定律来解释：回想一下，牛顿的第三定律指出，当物体 A 对物体 B 施加力时，物体 B 对物体 A 施加相等且相反的力。当入射波碰到墙壁时，弦向墙施加向上的力，墙做出反应通过对弦施加相等和相反的力。 固定边界处的反射是反向的。 请注意，该图显示了作为低谷反射的入射波的波峰。 如果入射波是低谷，则反射波将成为波峰。

    \(\PageIndex{1b}\)该图显示了自由边界条件。 在这里，绳子的一端被绑在无摩擦杆上的质量可以忽略不计的实心环上，因此琴弦的末端可以自由上下移动。 当入射波碰到介质的边界时，它也会被反射。 在自由边界条件下，反射波相对于入射波是同相的。 在这种情况下，波浪遇到自由边界，对环施加向上的力，使环向上加速。 环向上移动到等于波浪振幅的最大高度，然后由于弦中的张力向下加速至平衡位置。 该图显示入射波的波峰作为波峰相对于入射波相位反射。 如果入射波是低谷，那么反射波也将是一个低谷。 反射波的振幅将等于入射波的振幅。

    在某些情况下，介质的边界既不是固定的，也不是自由的。 以图（Figure）为例\(\PageIndex{2a}\)，其中，低线性质量密度串连接到线性质量密度更高的串上。 在这种情况下，反射波相对于入射波不相位。 还有一个发射波相对于入射波是同位的。 透射波和反射波的振幅都小于入射波的振幅。 如果两根弦的张力相同，则线性质量密度较低的弦中的波速会更高。

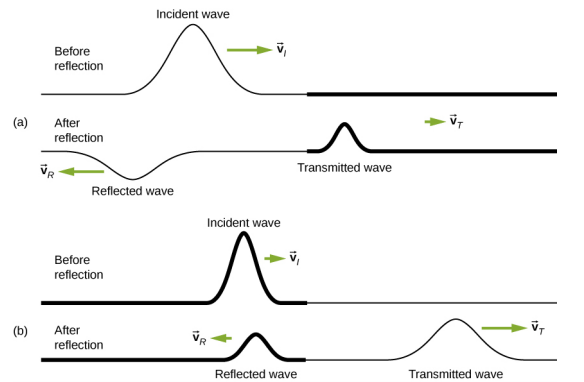
    图 a 显示了两根字符串，上面的一根标记为反射前，底部标记为反射后。 顶部字符串有一个标为入射波的脉冲，它以 velocity v 下标 i 向右传播。底部字符串有两个脉冲。 左边的那个标有发射波。 它以 velocity v 下标 T 向右传播。左边的波浪被标记为反射波。 它以 velocity v 下标 R 向左移动。它与入射波的振幅较小，并且是颠倒的。 图 b 显示了两根字符串，上面的一根标记为反射前，底部标记为反射后。 顶部字符串有一个标为入射波的脉冲，它以 velocity v 下标 i 向右传播。底部字符串有两个脉冲。 左边的那个被标记为透射波，右边的那个被标记为反射波。 两者都形成在字符串的顶部。
    图\(\PageIndex{2}\)：波浪沿着两种类型的弦传播：具有高线性密度的粗弦和具有低线性密度的细绳。 两根弦的张力相同，因此波浪在低密度弦上的移动速度比在高密度弦上移动得更快。 (a) 波从低速介质移动到高速介质会产生相对于入射脉冲（或波浪）相位180°（\(\pi\)rad）的反射波，以及与入射波同相的发射波。 (b) 当波浪从低速介质移动到高速介质时，反射波和发射波相对于入射波是相位的。

    \(\PageIndex{2b}\)显示高线性质量密度串连接到线性密度较低的字符串上。 在这种情况下，反射波相对于入射波是同位的。 还有一个发射波相对于入射波是同位的。 入射波和反射波的振幅都小于入射波的振幅。 在这里，你可能会注意到，如果两根弦的张力相同，则弦中的波速会更高，线性质量密度越低。

    叠加和干扰

    大多数波浪看起来并不很简单。 复杂的波浪更有趣，甚至更漂亮，但它们看起来很强大。 最有趣的机械波由在同一介质中传播的两个或多个行波的组合组成。 叠加原理可用于分析波浪的组合。

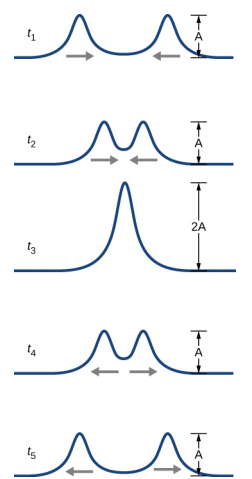
    假设两个振幅相同的简单脉冲在同一介质中相互移动，如图所示\(\PageIndex{3}\)。 最终，波浪重叠，产生振幅为两倍的波浪，然后继续前进，不受遭遇的影响。 据说脉冲会干扰，这种现象被称为干扰。

    五个数字显示了两个脉冲相互移动的不同阶段。 在时间 t1 时，脉冲相距很远。 两者都有振幅 A。它们在时间 t2 时相互移动，合并成具有两个峰值的波浪。 在时间 t3 时，它们合并成振幅为 2A 的单波。 在时间 t4 时，它们再次分开，各自恢复振幅 A。它们在时间 t5 时回到原来的位置。
    图\(\PageIndex{3}\)：两个相互移动的脉冲会受到干扰。 “干扰” 一词是指当两个波浪重叠时发生的情况。

    为了分析两个或多个波浪的干扰，我们使用叠加原理。 对于机械波，叠加原理指出，如果两个或多个行波在同一点合并，则介质质量元素在该点的结果位置是单个波浪产生的位置的代数和。 观察到的许多波浪都表现出这种特性，例如弦上的波浪、声波和地表水波。 电磁波也遵循叠加原理，但是添加了组合波的电场和磁场，而不是介质的位移。 遵守叠加原理的波浪是线性波；不遵守叠加原理的波浪被称为非线性波。 在本章中，我们将讨论线性波，特别是正弦波。

    通过考虑线性波动方程可以理解叠加原理。 在《波浪数学》中，我们将线性波定义为其数学表示遵循线性波动方程的波浪。 对于具有弹性恢复力的弦上的横向波，线性波动方程为

    \[\frac{\partial^{2} y(x,t)}{\partial x^{2}} = \frac{1}{v^{2}} \frac{\partial^{2} y(x,t)}{\partial t^{2}} \ldotp\]

    任何波函数 y (x, t) = y (x vt)，其中函数的参数是线性的 (x vt)，都是线性波动方程的解，是一个线性波函数。 如果波函数 y 1 (x, t) 和 y 2 (x, t) 是线性波动方程的解，则两个函数 y 1 (x, t) + y 2 (x, t) 的总和也是线性波动方程的解。 服从叠加的机械波通常仅限于振幅相对于其波长较小的波浪。 如果振幅太大，则介质会失真超过介质恢复力为线性的区域。

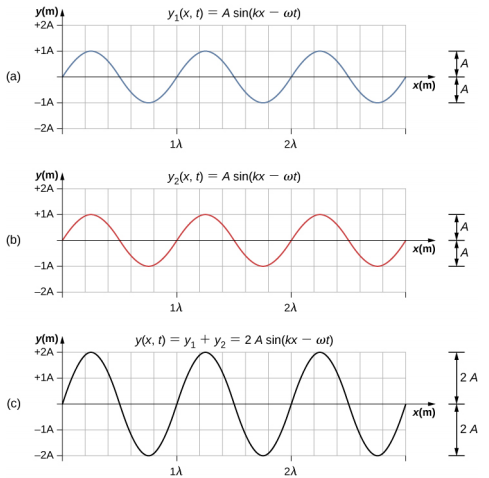
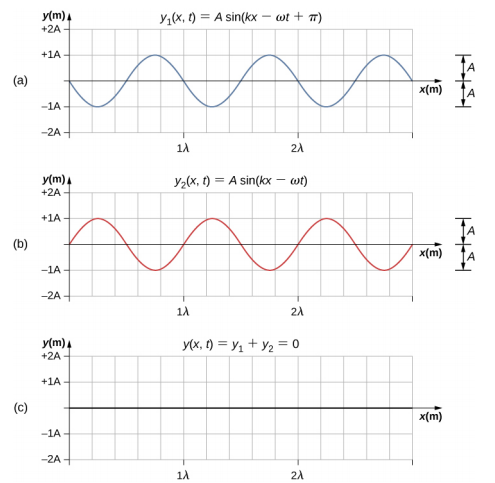
    波浪可以建设性地或破坏性地干扰。 图中\(\PageIndex{4}\)显示了两个相同的正弦波，它们正好相位到达同一点。 图\(\PageIndex{4a}\)中\(\PageIndex{4b}\)显示了两个单独的波浪，图中\(\PageIndex{4c}\)显示了由两个线性波的代数和产生的合成波浪。 两个波浪的波峰精确对齐，低谷也是如此。 这种叠加会产生建设性的干扰。 由于干扰加在一起，构造干扰产生的波浪振幅是单个波浪的两倍，但波长相同。

    图 a 和 b 分别显示了振幅 A 和波长 lambda 的波浪。 它们彼此处于同步。 图 a 被标记为 y1 括号 x，t 括号等于 A 正弦圆括号 kx 减去 omega t 括号。 图 b 被标记为 y2 括号 x，t 括号等于 A 正弦圆括号 kx 减去 omega t 括号。 图 c 显示了与其他两个波浪同相的波浪。 它的振幅为 2A，波长为 lambda。 它被标记为 y 括号 x，t 括号等于 y1 加 y2 等于 2A 正弦圆括号 kx 减去 omega t 括号。
    图\(\PageIndex{4}\)：两个相同波浪的构造干扰产生的波幅是原来的两倍，但波长相同。

    图中\(\PageIndex{5}\)显示了两个相同的波浪正好错相180°，产生了破坏性干扰。 绘制\(\PageIndex{5a}\)和\(\PageIndex{5b}\)显示单个波浪，图中\(\PageIndex{5c}\)显示了两个波浪的叠加。 由于一个波浪的波谷会增加另一个波浪的波峰，因此破坏性干扰产生的振幅为零——波浪完全抵消。

    图 a 和 b 分别显示了振幅 A 和波长 lambda 的波浪。 它们彼此之间相位偏离了一个角度 pi。 图 a 被标记为 y1 括号 x，t 括号等于 A 正弦圆括号 kx 减去 omega t 加 pi 括号。 图 b 被标记为 y2 括号 x，t 括号等于 A 正弦圆括号 kx 减去 omega t 括号。 图 c 显示没有任何波浪。 它被标记为 y 括号 x，t 括号等于 y1 加上 y2 等于 0。
    图\(\PageIndex{5}\)：两个相同波浪的破坏性干扰，其中一个波相移为 180° (\(\pi\)rad)，产生零振幅或完全抵消。

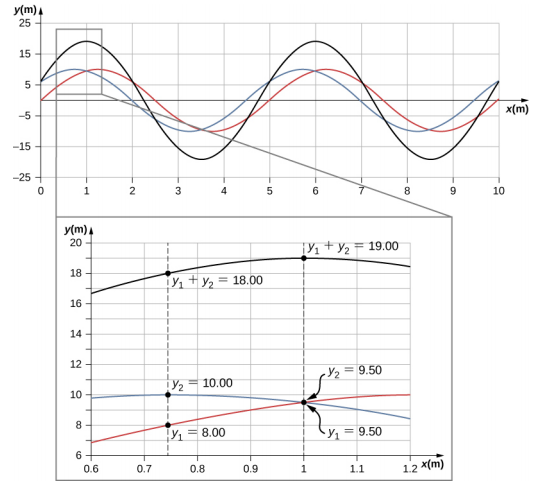
    当线性波干扰时，合成的波浪只是叠加原理中所述单个波浪的代数和。 图中\(\PageIndex{6}\)显示了两个波浪（红色和蓝色）和合成的波浪（黑色）。 生成的波浪是两个单独波浪的代数和。

    图中显示了三个波浪。 其中两个，蓝色和红色 y 值从 -10 到加 10 不等，波长相同。 它们稍微偏离了相位。 第三个是黑色，波长相同，但振幅更大。 另一个图显示了这张图的爆炸部分。 在 x 大约等于 0.74 时，红色和蓝色波浪的 y 值分别为 y1 = 8 和 y2 = 10。 黑波的 y 值为 y1 + y2 = 18。 在 x 等于 1 时，红色和蓝色波浪的 y 值均为 9.5。 黑波的 y 值为 y1 + y2 = 19。
    图\(\PageIndex{6}\)：当同一介质中的两个线性波相互干扰时，生成的波浪的高度是逐点拍摄的各个波浪高度的总和。 此图显示了两个波浪（红色和蓝色）相加在一起以及生成的波浪（黑色）。 这些图表示波浪在每个点的高度。 波浪可以是任何线性波，包括池塘上的波浪、弦上的干扰、声音或电磁波。

    大多数波浪的叠加会产生建设性和破坏性干扰的组合，并且可能因地点和时间而异。 例如，立体声系统发出的声音在一个位置可能很响亮，而在另一个位置可以很安静。 不同的响度意味着声波在不同的位置增加部分建设性的，部分是破坏性的。 立体声音响至少有两个扬声器产生声波，波浪可以从墙壁反射。 所有这些波浪都会干扰，由此产生的波浪是波浪的叠加。

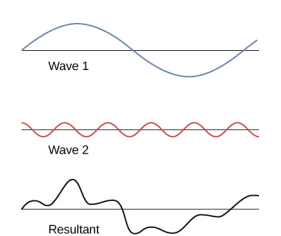
    我们已经展示了几个相似的波浪叠加的例子。 该\(\PageIndex{7}\)图显示了两个不同波浪的叠加示例。 在这里，干扰又增加了，产生了由此产生的波浪。

    图中显示了三个波浪。 与波浪2相比，波浪1的波长和振幅更大。 第三波被标记为合成波浪形状不规则。
    图\(\PageIndex{7}\)：不同波浪的叠加表现出建设性和破坏性干扰。

    有时，当两个或两个以上的机械波干扰时，由此产生的波浪产生的模式可能非常复杂，有些没有任何容易辨别的模式。 例如，绘制你最喜欢的音乐的声波可能看起来相当复杂，是来自许多乐器的单个声波的叠加；正是这种复杂性使音乐变得有趣且值得一听。 在其他时候，波浪会干扰并产生有趣的现象，这些现象在外观上很复杂，但与形成波浪的叠加物理原理相比却很漂亮。 一个例子是被称为驻波的现象，它是由两个向不同方向移动的相同波浪产生的。 我们将在下一节中更仔细地研究这种现象。

    模拟

    试试这个模拟，用滴水的水龙头、音频扬声器或激光制造波浪！ 添加第二个源或一对狭缝以创建干扰图案。 你可以观察一个或两个来源。 使用两个信号源，您可以观察由于信号源的频率和振幅变化而产生的干扰模式。

    叠加因相移而不同的正弦波

    物理学中的许多例子由两个正弦波组成，它们的振幅、波数和角频率相同，但因相移而不同：

    \[\begin{split} y_{1} (x,t) & = A \sin (kx - \omega t + \phi), \\ y_{2} (x,t) & = A \sin (kx - \omega t) \ldotp \end{split}\]

    当这两个波浪存在于同一个介质中时，两个单独波浪的叠加所产生的波浪是两个单独波浪的总和：

    \[y_{R} (x,t) = y_{1} (x,t) + y_{2} (x,t) = A \sin(kx - \omega t + \phi) + A \sin (kx - \omega t) \ldotp\]

    使用三角恒等式可以更好地理解生成的波浪：

    \[\sin u + \sin v = 2 \sin \left(\dfrac{u + v}{2}\right) \cos \left(\dfrac{u - v}{2}\right),\]

    其中 u = kx-\(\omega\) t +\(\phi\) 和 v = kx-\(\omega\) t。生成的波浪变成

    \[\begin{split} y_{R} (x,t) & = y_{1} (x,t) + y_{2} (x,t) = A \sin (kx - \omega t + \phi) + A \sin (kx - \omega t) \\ & = 2A \sin \left(\dfrac{(kx - \omega t + \phi) + (kx - \omega t)}{2}\right) \cos \left(\dfrac{(kx - \omega t + \phi) - (kx - \omega t)}{2}\right) \\ & = 2A \sin \left(kx - \omega t + \dfrac{\phi}{2}\right) \cos \left(\dfrac{\phi}{2}\right) \ldotp \end{split}\]

    这个方程通常写成

    \[y_{R} (x,t) = 2A \cos \left(\dfrac{\phi}{2}\right) \sin \left(kx - \omega t + \dfrac{\phi}{2}\right) \ldotp \label{16.13}\]

    合成的波具有相同的波数和角频率，振幅为 A R = [2A cos\(\left(\dfrac{\phi}{2}\right)\)]，相移等于原始相移的一半。 图中显示了仅在相移中存在差异的波浪示例\(\PageIndex{7}\)。

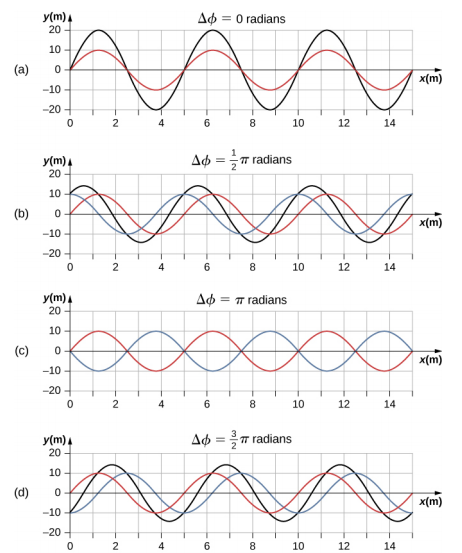
    弧度。 蓝波的波峰与红波的波谷重合，反之亦然。 绿浪不存在。 图 d 被标记为 delta phi 等于 3 pi 乘 2 弧度。 在这里，红波和蓝波的振幅各为 10 m，绿色波浪的振幅为 15 m。它与其他两个波浪的波长相同。 绿色波浪的波峰是在红色和蓝色波浪的波峰相互交叉的地方形成的。
    图\(\PageIndex{8}\)：两个波的叠加，其振幅、波长和频率相同，但相移不同。 红色波浪由波函数 y 1 (x, t) = A sin (kx −\(\omega\) t) 定义，蓝波由波函数 y 2 (x, t) = A sin (kx −\(\omega\) t +\(\phi\)) 定义。 黑线显示两个波浪相加的结果。 两个波浪之间的相位差为 (a) 0.00 rad、(b)\(\frac{\pi}{2}\) rad、(c)\(\pi\) rad 和 (d)\(\frac{3 \pi}{2}\) rad。

    红色和蓝色波浪的振幅、波数和角频率各相同，仅在相移方面有所不同。 因此，它们具有相同的周期、波长和频率。 绿色波浪是两个波浪叠加的结果。 当两个波的相位差为零时，波浪处于同相，合成的波浪具有相同的波数和角频率，振幅等于单个振幅的两倍（第（a）部分）。 这是建设性的干预。 如果相位差为 180°，则波浪会干扰破坏性干扰（第 (c) 部分）。 生成的波浪振幅为零。 任何其他相位差都会产生与两个入射波具有相同波数和角频率的波浪，但相移为，振幅等于 2A cos\(\left(\dfrac{\phi}{2}\right)\)。\(\frac{\phi}{2}\) 例子见第 (b) 和 (d) 部分。