16.5: 波浪的能量和力量

Last updated
Save as PDF

Page ID: 204277

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

解释能量如何随脉冲或波浪传播
使用数学表达式描述波浪中的能量如何取决于波浪的振幅

所有波浪都携带能量，有时可以直接观察到这种能量。地震可以将整个城市震倒在地，使成千上万的破坏球起作用（图$\PageIndex{1}$）。响亮的声音会粉碎内耳的神经细胞，导致永久性听力损失。超声波用于肌肉拉伤的深层热治疗。激光束可以烧掉恶性肿瘤。水浪吞噬了海滩。

地震损坏的财产。许多建筑物倒塌了。 — 图$\PageIndex{1}$：地震的破坏性影响是这些海浪携带能量的明显证据。地震的里氏等级评级是与地震的振幅和所携带的能量相关的对数标度。

在本节中，我们将研究波浪中能量的定量表达。这在以后关于波浪的讨论中至关重要，从声到光再到量子力学。

波浪中的能量

波浪中的能量与其振幅和频率有关。大振幅地震会产生较大的地面位移。与柔和的声音相比，响亮的声音具有高压振幅，并且来自更大的振幅源振动。大型海上破碎船比小型破海船更能搅动岸边。以本章前面的海鸥和水浪为例（图 16.2.2）。随着海鸥向上移动，海鸥的作用由海鸥完成，改变了它的潜在能量。振幅越大，海鸥被海浪抬起的越高，势能的变化就越大。

波浪的能量取决于振幅和频率。如果将每个波长的能量视为离散的能量包，则高频波在单位时间内将比低频波传送更多的此类数据包。我们将看到，机械波中的平均能量传递速率与振幅的平方和频率的平方成正比。如果两个机械波的振幅相等，但一个波的频率等于另一个波的频率的两倍，则较高频率波的能量传递速率将是低频波能量传递速率的四倍。应该注意的是，尽管能量传输速率与机械波振幅的平方和频率的平方成正比，但电磁波中的能量传递速率与振幅的平方成正比，但与频率无关。

波浪中的力量

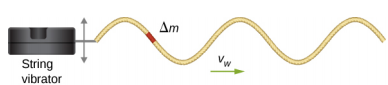
以弦振动器产生的弦上的正弦波为例，如图所示$\PageIndex{2}$。弦振动器是一种上下振动棒的装置。一串均匀的线性质量密度附着在杆上，杆使弦振荡，产生正弦波。棒确实在弦上起作用，产生沿着绳子传播的能量。假设字符串中质量为$\Delta$ m 的质量元素，如图所示$\PageIndex{2}$。当能量沿着弦传播时，弦的每个质量元素都以与波浪相同的频率上下驱动。弦的每个质量元素都可以建模为一个简单的谐波振荡器。由于字符串具有恒定的线性密度$\mu = \frac{\Delta m}{\Delta x}$，因此字符串的每个质量元素的质量为$\Delta$ m =$\mu \Delta$ x。

图中左侧显示了一个标有弦振动器的盒子。上面附着一根字符串，形成横向波，向右传播，速度为 v 下标 w。字符串的一小部分被突出显示并标记为 delta m。 — 图$\PageIndex{2}$：弦振器是一种振动棒的装置。一根绳子固定在杆上，杆确实在绳子上起作用，使绳子上下移动。这会在弦中产生一个正弦波，它以波速 v 移动。波速取决于弦中的张力和弦的线性质量密度。质量为$\Delta$ m 的弦段振荡频率与波浪的振荡频率相同。

波浪的总机械能是其动能和势能的总和。长度为$\Delta$ x 的字符串中每个质量元素的动能$\Delta$ K =$\frac{1}{2}$ mv ² 为 K =$\frac{1}{2}$ ($\Delta$m) v _y ²，因为质量元素垂直于波浪的运动方向振荡。使用恒定线性质量密度，长度为$\Delta$ x 的弦中每个质量元素的动能为

\[\Delta K = \frac{1}{2} (\mu \Delta x) v_{y}^{2} \ldotp \nonumber \]

微分方程可以通过让字符串的质量元素的长度接近零来形成，

\[dK = \lim_{\Delta x \rightarrow 0} \frac{1}{2} (\mu \Delta x) v_{y}^{2} = \frac{1}{2} (\mu\; dx)v_{y}^{2} \ldotp \nonumber \]

由于波是具有角频率的正弦波$\omega$，因此每个质量元素的位置可以建模为 y (x, t) = A sin (kx −$\omega$ t)。弦中的每个质量元素都以速度 v _y$\frac{\partial y(x,t)}{\partial t}$ = −A$\omega$ cos (kx −$\omega$ t) 振荡。弦中每个质量元素的动能变成

\[\begin{split} dK & = \frac{1}{2} (\mu\; dx)[-A \omega \cos(kx - \omega t)]^{2} \\ & = \frac{1}{2} (\mu\; dx)[A^{2} \omega^{2} \cos^{2}(kx - \omega t)] \ldotp \end{split}\]

波浪可能很长，由许多波长组成。要对能量进行标准化，请考虑与波长相关的动能。这种动能可以在波长上进行积分，以找到与波浪的每个波长相关的能量：

\[\begin{split} dK & = \frac{1}{2} (\mu\; dx)[A^{2} \omega^{2} \cos^{2}(kx - \omega t)] \\ \int_{0}^{K_{\lambda}} dK & = \int_{0}^{\lambda} \frac{1}{2} \mu A^{2} \omega^{2} \cos^{2}(kx - \omega t) dx = \frac{1}{2} \mu A^{2} \omega^{2} \int_{0}^{\lambda} \cos^{2} (kx) dx, \\ K_{lambda} & = \frac{1}{2} \mu A^{2} \omega^{2} \Big[ \frac{1}{2} x + \frac{1}{4k} \sin (2kx) \Big]_{0}^{\lambda} \\ & = \frac{1}{2} \mu A^{2} \omega^{2} \Big[ \frac{1}{2} \lambda + \frac{1}{4k} \sin (2k \lambda) - \frac{1}{4k} \sin(0) \Big] \\ & = \frac{1}{4} \mu A^{2} \omega^{2} \lambda \ldotp \end{split}\]

还有与波浪相关的潜在能量。就像弹簧上的质量振荡一样，有一种保守的恢复力，当质量元素偏离平衡位置时，它会将质量元素带回平衡位置。质量元素的势能可以通过考虑弦的线性恢复力来找到。在《振荡》中，我们看到存储在具有线性恢复力的弹簧中的势能等于 U =$\frac{1}{2}$ k _s x ²，其中平衡位置定义为 x = 0.00 m。当附着在弹簧上的质量在简单的谐波运动中振荡时，角频率等于$\omega = \frac{k_{s}}{m}$。当每个质量元件在简单的谐波运动中振荡时，弹簧常数等于 k _s =$\Delta$ m$\omega^{2}$。质量元素的势能等于

\[\Delta U = \frac{1}{2} k_{s} x^{2} = \frac{1}{2} \Delta m \omega^{2} x^{2} \ldotp \nonumber \]

注意 k _s 是弹簧常数，而不是波数 k =$\frac{2 \pi}{\lambda}$。该方程可用于计算波长范围内的能量。通过对波长进行积分，我们可以计算出波长范围内的势能：

\[\begin{split} dU & = \frac{1}{2} k_{s} x^{2} = \frac{1}{2} \mu \omega^{2} x^{2} dx, \\ U_{\lambda} & = \frac{1}{2} \mu \omega^{2} A^{2} \int_{0}^{\lambda} \sin^{2} (kx) dx = \frac{1}{4} \mu A^{2} \omega^{2} \lambda \ldotp \end{split}\]

与波长相关的势能等于与波长相关的动能。与波长相关的总能量是势能和动能之和：

\[\begin{split} E_{\lambda} & = U_{\lambda} +K_{\lambda} \\ & = \frac{1}{4} \mu A^{2} \omega^{2} \lambda + \frac{1}{4} \mu A^{2} \omega^{2} \lambda \\ & = \frac{1}{2} \mu A^{2} \omega^{2} \lambda \ldotp \end{split}\]

正弦机械波的时间平均功率，即波浪经过一个点时与之相关的平均能量传递速率，可以通过将与波浪相关的总能量除以传递能量所花费的时间来得出。如果正弦波的速度恒定，则一个波长经过一个点的时间等于波的周期，后者也是恒定的。因此，对于正弦机械波，时间平均功率等于与波长相关的能量除以波浪周期。波浪的波长除以周期等于波浪的速度，

\[P_{ave} = \frac{E_{\lambda}}{T} = \frac{1}{2} \mu A^{2} \omega^{2} \frac{\lambda}{T} = \frac{1}{2} \mu A^{2} \omega^{2} v \ldotp \label{16.10}\]

请注意，这个正弦机械波的时间平均功率方程表明，功率与波浪振幅的平方和波浪角频率的平方成正比。回想一下，角频率等于$\omega$ = 2$\pi$ f，因此机械波的功率等于振幅的平方和波频率的平方。

示例 16.6：由弦振动器提供的电力

假设一根两米长、质量为 70.00 g 的绳子连接到弦式振动器上，如图所示$\PageIndex{2}$。弦中的张力为 90.0 N。当弦振动器开启时，它会以 60 Hz 的频率振荡，并在弦上产生振幅为 4.00 cm 且波速恒定的正弦波。弦振动器为波浪提供的时间平均功率是多少？

策略

提供给波浪的功率应等于弦上波浪的时间平均功率。我们知道弦的质量（m _s）、弦的长度（L _s）和弦中的张力（F _T）。弦上波浪的速度可以从线性质量密度和张力中得出。弦的振荡频率与弦振动器的振荡频率相同，我们可以从中找到角频率。

解决方案

从弦上正弦波的时间平均功率方程开始：$$P =\ frac {1} {2}\ mu A^ {2}\ omega^ {2} v\ ldotp$给出了振幅，所以我们需要计算弦的线性质量密度、弦上波浪的角频率和弦上波浪的速度。
我们需要计算线性密度才能找到波速：$$\ mu =\ frac {m_ {s}} {L_ {s}} =\ frac {0.070\; kg} {2.00\; m} = 0.035\; kg/m\ ldotp$$
波速可以通过线性质量密度和弦的张力来找到：$$v =\ sqrt {\ frac {F_ {T}} {\ mu}} =\ sqrt {\ frac {90.00\; N} {0.035\; kg/m}} = 50.71\; m/s\ ldotp$$
角频率可以从频率中找到：$$\ omega = 2\ pi f = 2\ pi (60\; s^ {-1}) = 376.80\; s^ {-1}\ ldotp$$
计算时间平均功率：$$P =\ frac {1} {2}\ mu A^ {2}\ omega^ {2} v =\ frac {1} {2} (0.035\; kg/m) (0.040\; m) ^ {2} (376.80\; s^ {-1}) ^ {2} (50.71\; m/s) = 201.5\; W\ l dotp$$

意义

正弦波的时间平均功率与波浪振幅的平方和波的角频率的平方成正比。大多数机械波都是如此。如果将波浪的角频率或振幅加倍，则功率将增加四倍。弦上波浪的时间平均功率也与弦上正弦波的速度成正比。如果速度提高一倍，将张力提高四倍，则功率也将增加一倍。

练习 16.6

弦上正弦波的时间平均功率是否与弦的线性密度成正比？

波浪能量方程和时间平均功率方程是针对弦上正弦波得出的。通常，机械波的能量和功率与振幅的平方和角频率的平方（因此也是频率的平方）成正比。

波浪的另一个重要特征是波浪的强度。波浪也可以集中或散开。例如，地震产生的波浪在远离源头时会散布在更大的区域，因此它们离源头越远，造成的伤害就越小。改变海浪覆盖的区域具有重要影响。所有这些相关因素都包含在单位面积功率的强度 (I) 的定义中：

\[I = \frac{P}{A}, \label{16.11}\]

其中 P 是波浪通过区域 A 所携带的功率。强度的定义适用于传输中的任何能量，包括波浪携带的能量。强度的 SI 单位是瓦特每平方米 (W/m ²)。许多波浪是球形波，像球体一样从源头移出。例如，安装在地面上方柱上的扬声器可能会产生像球形波一样远离声源的声波。下一章将更详细地讨论声波，但总的来说，你离扬声器越远，你听到的声音就越不强烈。当球形波从源头移出时，波浪的表面积会随着半径的增加而增加（A = 4$\pi$ r ²）。因此，球形波的强度为

\[I = \frac{P}{4 \pi r^{2}} \ldotp \label{16.12}\]

如果没有耗散力，则当球形波离开源时，能量将保持不变，但强度将随着表面积的增加而降低。

对于二维圆波，波浪向外移动，随着圆半径的增加，波浪的周长会增加。如果你在池塘里扔鹅卵石，表面波纹会像圆波一样向外移动。当波纹远离源时，振幅会减小。波浪的能量围绕更大的周长扩散，振幅的减小与球形波成正比$\frac{1}{r^{2}}$，而不是像球形波那样。$\frac{1}{r}$