16.4: 拉伸绳上的波速

Last updated
Save as PDF

Page ID: 204298

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

确定影响弦上波浪速度的因素
为字符串上波浪的速度写一个数学表达式，并将这些概念推广到其他媒体中

波浪的速度取决于介质的特性。例如，对于吉他，琴弦会振动以产生声音。琴弦上波浪的速度和波长决定了发出的声音的频率。吉他上的琴弦有不同的厚度，但可能由相似的材料制成。它们具有不同的线性密度，其中线性密度定义为每长度的质量，

\[\mu = \frac{\text{mass of string}}{\text{length of string}} = \frac{m}{l} \ldotp \label{16.7}\]

在本章中，我们只考虑具有恒定线性密度的字符串。如果线性密度恒定，则小长度的字符串 ($\Delta m$$\Delta$x) 的质量 () 为$\Delta m = \mu \Delta x$。例如，如果绳子的长度为 2.00 m，质量为 0.06 kg，则线性密度为$\mu = \frac{0.06\; kg}{2.00\; m}$ = 0.03 kg/m。如果从绳子上切出 1.00 毫米的截面，则 1.00 毫米长度的质量为

\[ \Delta m = \mu \Delta x = (0.03\, kg/m)(0.001\, m) = 3.00 \times 10^{−5}\, kg. \nonumber\]

吉他还有一种改变琴弦张力的方法。琴弦的张力是通过旋转主轴（称为调音钉）来调整的，琴弦缠绕在主轴周围。对于吉他来说，弦的线性密度和弦中的张力决定了弦中波浪的速度，而产生的声音的频率与波速成正比。

张力下弦上的波速

要了解弦上波浪的速度如何取决于张力和线性密度，可以考虑沿着拉紧的绳子发出的脉冲（图$\PageIndex{1}$）。当拉紧的琴弦处于平衡位置时，琴弦中的张力$F_T$是恒定的。假设字符串中质量等于的小元素$\Delta m = \mu \Delta x$。质量元素处于静止状态和平衡状态，质量元素两侧的张力相等且相反。

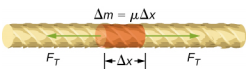
该图显示了字符串的一部分，其中一部分突出显示。突出显示部分的长度被标记为 delta x。该部分的两个箭头沿着字符串的长度指向相反的方向。它们被标记为 F 下标 T。突出显示的部分被标记为 delta m 等于 mu delta x。 — 图$\PageIndex{1}$：绳子的质量元素在张力下保持拉紧$F_T$。质量元素处于静态平衡状态，作用在质量元素两侧的张力大小相等，方向相反。

如果你在张力下拔出一根绳子，横向波会向正 x 方向移动，如图所示$\PageIndex{2}$。质量元素很小，但在图中放大了以使其可见。由于弦提供的恢复力，小质量元素垂直于波浪运动振荡，并且不会在 x 方向上移动。弦中的张力 F _T 在 x 方向和正 x 方向上起作用，近似恒定，与位置和时间无关。

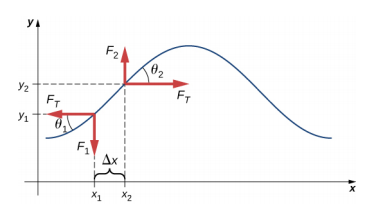
图中显示了脉冲波。沿着波浪的向上斜率显示了两个箭头，一个指向上和向右，另一个指向下和向左。这些标有 F 的箭头分别使用 theta 2 和 theta 1 形成角度 — 图$\PageIndex{2}$：一根受拉的绳子被弹出，使脉冲沿着弦向正 x 方向移动。

假设移位的弦相对于水平轴的倾角很小。与弦平行作用的弦元素上的净力是弦中张力和恢复力的总和。张力的 x 分量取消，因此净力等于力的 y 分量之和。力的 x 分量的大小等于弦的水平张力，$F_T$如图所示$\PageIndex{2}$。要获得力的 y 分量，请注意棕褐色$\theta_{1} = − \frac{F_{1}}{F_{T}}$和$\tan \theta_{2} = \frac{F_{2}}{F_{T}}$。等$\tan \theta$于某个点处函数的斜率，等于该点上 y 相对于 x 的偏导数。因此，等$\frac{F_{1}}{F_{T}}$于 x ₁ 处字符串的负斜率，等$\frac{F_{2}}{F_{T}}$于 x ₂ 处字符串的斜率：

\[\frac{F_{1}}{F_{T}} = - \left(\dfrac{\partial y}{\partial x}\right)_{x_{1}}\; and\; \frac{F_{2}}{F_{T}} = \left(\dfrac{\partial y}{\partial x}\right)_{x_{2}} \ldotp\]

小质量元素上的净力可以写成

\[F_{net} = F_{1} + F_{2} = F_{T} \Bigg[ \left(\dfrac{\partial y}{\partial x}\right)_{x_{2}} - \left(\dfrac{\partial y}{\partial x}\right)_{x_{1}} \Bigg] \ldotp\]

使用牛顿第二定律，净力等于质量乘以加速度。弦的线性密度 μ 是弦每长度的质量，而弦部分的质量为$\mu \Delta$ x，

\[F_{T} \Bigg[ \left(\dfrac{\partial y}{\partial x}\right)_{x_{2}} - \left(\dfrac{\partial y}{\partial x}\right)_{x_{1}} \Bigg] = \Delta ma = \mu \Delta x \left(\frac{\partial^{2} y}{\partial t^{2}}\right) \ldotp\]

除以 F _T$\Delta$ x 并在$\Delta$ x 接近零时取极限，

\[\begin{split} \lim_{\Delta x \rightarrow 0} \frac{\Bigg[ \left(\dfrac{\partial y}{\partial x}\right)_{x_{2}} - \left(\dfrac{\partial y}{\partial x}\right)_{x_{1}} \Bigg]}{\Delta x} & = \frac{\mu}{F_{T}} \frac{\partial^{2} y}{\partial t^{2}} \\ \frac{\partial^{2} y}{\partial x^{2}} & = \frac{\mu}{F_{T}} \frac{\partial^{2} y}{\partial t^{2}} \ldotp \end{split}\]

回想一下，线性波动方程是

\[\frac{\partial^{2} y(x,t)}{\partial x^{2}} = \frac{1}{v^{2}} \frac{\partial^{2} y(x,t)}{\partial t^{2}} \ldotp\]

因此，

\[\frac{1}{v^{2}} = \frac{\mu}{F_{T}} \ldotp\]

求解一$v$下，我们发现弦上波浪的速度取决于张力和线性密度

张力下弦上波浪的速度

拉伸下弦上脉冲或波浪的速度可以通过以下方程式得出

\[|v| = \sqrt{\frac{F_{T}}{\mu}} \label{16.8}\]

其中，$F_T$是弦中的张力$µ$，是琴弦每长度的质量。

示例 16.5：吉他弹簧的波速

在六弦吉他上，高 E 弦的线性密度为$\mu_{High\; E}$ = 3.09 x 10 ⁻⁴ kg/m，低 E 弦的线性密度为$\mu_{Low\; E}$ = 5.78 x 10 ⁻³ kg/m。(a) 如果弹奏高 E 弦在琴弦中产生波浪，则波浪的速度是多少琴弦的张力为 56.40 N？ (b) 低 E 弦的线性密度大约是高 E 弦的 20 倍。要使波浪以与高 E 弦相同的波速穿过低 E 弦，张力需要比高 E 弦大还是小？大概的张力是多少？ (c) 计算相同波速所需的低 E 弦的张力。

策略

波的速度可以从线性密度和张力中得出$v = \sqrt{\frac{F_{T}}{\mu}}$。
根据方程 v =$\sqrt{\frac{F_{T}}{\mu}}$，如果线性密度增加近 20 倍，则张力需要增加 20 倍。
知道速度和线性密度，就可以求解张力 F _T =$\mu$ v ² 的速度方程。

解决方案

使用速度方程求出速度：$$v =\ sqrt {\ frac {F_ {T}} {\ mu}} =\ sqrt {\ frac {56.40\; N} {3.09\ times 10^ {-4}\; kg/m}} = 427.23\; m/s\ ldotp$$
紧张局势需要增加大约20倍。张力将略小于 1128 N。
使用速度方程求出实际张力：$$F_ {T} =\ mu v^ {2} = (5.78\ times 10^ {-3}\; kg/m) (427.23\; m/s) ^ {2} = 1055.00\; N\ ldotp$$
该解在近似值的 7% 以内。

意义

六弦的标准音符（高 E、B、G、D、A、低 E）经过调整，在弹奏时以基本频率（329.63 Hz、246.94 Hz、196.00 Hz、146.83 Hz、110.00 Hz 和 82.41 Hz）振动。频率取决于弦上波浪的速度和波浪的波长。六根弦具有不同的线性密度，通过改变琴弦的张力进行 “调整”。我们将在《波浪干扰》中看到，波长取决于弦的长度和边界条件。要演奏基本音符以外的音符，可通过向下按琴弦来改变琴弦的长度。

练习 16.5

弦上波浪的波速取决于张力和线性质量密度。如果张力加倍，琴弦上波浪的速度会怎样？

流体中压缩波的速度

弦上波浪的速度取决于张力的平方根除以每长度的质量，即线性密度。通常，波浪穿过介质的速度取决于介质的弹性特性和介质的惯性特性。

\[|v| = \sqrt{\frac{elastic\; property}{inertial\; property}}\]

弹性特性描述了介质中的粒子在受到干扰时返回其初始位置的趋势。惯性特性描述了粒子抵抗速度变化的趋势。

纵波穿过液体或气体的速度取决于流体的密度和流体的体积模量，

\[v = \sqrt{\frac{\beta}{\rho}} \ldotp \label{16.9}\]

这里的体积模量定义为 Β =$− \frac{\Delta P}{\frac{\Delta V}{V_{0}}}$，其中$\Delta$ P 是压力的变化，分母是体积变化与初始体积的比率，$\rho \equiv \frac{m}{V}$是单位体积的质量。例如，声音是一种通过流体或固体传播的机械波。大气压为 1.013 x 10 ⁵ Pa、温度为 20°C 时，空气中的声速为 v _s β 343.00 m/s。由于密度取决于温度，因此空气中的声速取决于空气的温度。这将在声音中详细讨论。