16.3: 波浪数学

Last updated
Save as PDF

Page ID: 204315

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

使用数学表达式对以恒定波速运动的波浪进行建模
计算介质的速度和加速度
显示介质速度与波速（传播速度）有何不同

在上一节中，我们根据周期波的波长、周期、振幅和波速等特征描述了周期性波。波浪也可以用波浪移动的介质粒子的运动来描述。介质粒子的位置可以在数学上建模为波函数 s，它可用于随时查找波浪介质粒子的位置、速度和加速度。

脉冲

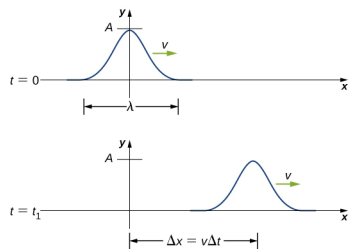
脉冲可以描述为由单一干扰组成的波，它以恒定的振幅在介质中移动。脉冲以一种模式移动，在以恒定的波速传播时保持其形状。由于波速是恒定的，脉冲在一段时间内移动的距离 Δt 等于 Δx = vαT（图$\PageIndex{1}$）。

使用波函数对一维正弦波进行建模

假设一根绳子保持恒定张力，$F_T$其中一端是固定的，自由端$y = −A$由机械设备以恒定频率在$y = +A$和之间振荡。图中$\PageIndex{2}$显示了波浪的快照，间隔为八分之一周期，在一个周期之后开始（$t = T$）。

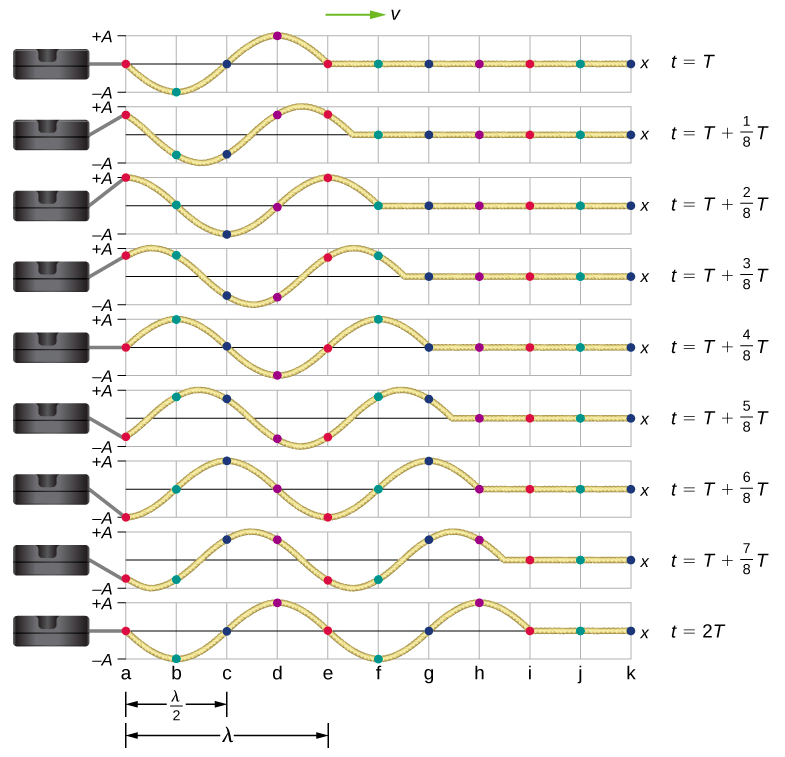
该图显示了横向波向右传播的不同阶段，间隔为 1 x 8 T。点标记波浪上的点。它们从 — A 到 +A 上下移动。在时间 t=t 处处于平衡位置的点，在时间 t=t 加 2 x 8 T 时移动到 +A，然后它在时间 t= T 加 4 x 8 T 时移回平衡位置，在时间 t=t 加 6 x 8 T 时移回平衡位置。同样，在时间 t=2t 时，所有点都会移动到其原始位置。 — 图$\PageIndex{2}$：横向波浪在张力下穿过绳子的快照，从时间$t = T$开始，间隔为$\frac{1}{8}T$。彩色圆点用于突出字符串上的点。在 x 方向上相隔一定波长的点用相同颜色的点突出显示。

请注意，字符串上的每个选择点（用彩色圆点标记）在简单的谐波运动中上下振荡，介于$y = +A$和之间$y = −A$，并带有句点$T$。弦上的波浪是正弦波，随着时间的推移，它在正 x 方向上平移。

此时，从你对代数的研究中回想一下，如果$f(x)$是某个函数，那么$f(x−d)$同一个函数在正 x 方向上平移了一段距离，这很有用$d$。该函数$f(x+d)$是在负的 x 方向上平移一段距离的同一个函数$d$。我们想定义一个波浪函数，它将每次给出字符串上每个$y$位置 x 的字符串每段的-position$t$。

查看图中的第一个快照$\PageIndex{2}$，$x = λ$可以将$x = 0$和之间的字符串的 y 位置建模为正弦函数。如上一张快照所示，该波浪在一个周期内沿着字符串向下传播一个波长。因此，波浪以恒定的波速移动$v = λ/T$。

回想一下，正弦函数是角度的函数$θ$，在 +1 和 −1 之间振荡，每隔一个$2π$弧度重复一次（图$\PageIndex{3}$）。但是，介质的 y 位置或波函数在$+A$和之间振荡$−A$，并在每个波长之间重复$λ$。

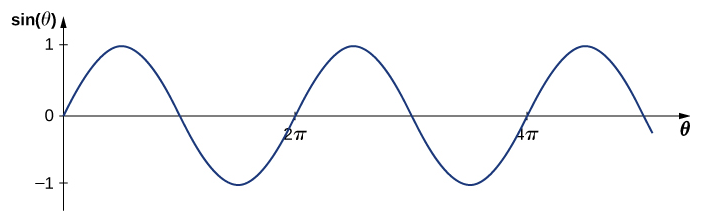
该图显示了在 y 轴上有正弦西塔，x 轴上有 theta 的图形。它看起来像横波，其 y 值从 -1 到 +1 不等。波浪的波峰值为 theta 等于 pi 乘 2，5 pi 乘以 2，依此类推。它在 0、pi、2 pi 等处穿过 x 轴。 — 图$\PageIndex{3}$：正弦函数每 2β 弧度在 +1 和 −1 之间振荡。

要使用周期函数构造我们的波浪模型，请考虑角度和位置的比率，

\[\begin{align*} \dfrac{\theta}{x} &=\frac{2 \pi}{\lambda}, \\[4pt] \theta &=\frac{2 \pi}{\lambda} x. \end{align*}\]

使用$\theta = \frac{2\pi}{\lambda}x$正弦函数乘以振幅 A，我们现在可以将字符串的 y 位置建模为位置 x 的函数：

\[ y(x)=A \sin \left(\frac{2 \pi}{\lambda} x\right). \nonumber \]

弦上的波浪以恒定速度 v 沿正 x 方向移动，并在时间 t 中移动距离 v t。波浪函数现在可以通过以下方式定义

\[ y(x, t)=A \sin \left(\frac{2 \pi}{\lambda}(x-v t)\right). \nonumber \]

以更紧凑的形式重写这个波浪函数通常很方便。乘以比率得$\frac{2\pi}{\lambda}$出方程

\[ y(x, t)=A \sin \left(\frac{2 \pi}{\lambda} x-\frac{2 \pi}{\lambda} v t\right). \nonumber \]

该值$\frac{2\pi}{\lambda}$被定义为波数。波数的符号为 k，单位为反米 m，m ⁻¹：

\[ k \equiv \frac{2 \pi}{\lambda} \label{16.2} \]

回想一下《振荡》中的角频率定义为$\omega \equiv \frac{2\pi}{T}$。波函数的第二个项变成

\[\frac{2 \pi}{\lambda} v t=\frac{2 \pi}{\lambda}\left(\frac{\lambda}{T}\right) t=\frac{2 \pi}{T} t=\omega t. \nonumber \]

弦上简单谐波的波函数简化为

\[ y(x, t)=A \sin (k x \mp \omega t) \nonumber \]

其中 A 是振幅，$k = \frac{2\pi}{\lambda}$是波数，$\omega = \frac{2\pi}{T}$是角频率，负号表示波浪在正 x 方向移动，加号表示波浪在负 x 方向移动。波浪的速度等于

\[ v=\frac{\lambda}{T}=\frac{\lambda}{T}\left(\frac{2 \pi}{2 \pi}\right)=\frac{\omega}{k} \label{16.3} .\]

回想一下我们对弹簧质量的讨论，当时质量的位置被建模为

\[x(t) = A \cos(ωt+ϕ). \nonumber\]

角度$ϕ$是相移，之所以添加这个角度是为了考虑到质量可能有$x = +A$和以外的初始条件$v = 0$。出于类似的原因，初始阶段被添加到波浪函数中。对正弦波进行建模、允许初始相移$ϕ$的波函数是

\[ y(x, t)=A \sin (k x \mp \omega t+\phi) \label{16.4} \]

价值

\[ (k x \mp \omega t+\phi) \label{16.5} \]

被称为波浪的相位，其中$\phi$是波函数的初始阶段。时间项$\omega t$是负数还是正取决于波浪的方向。首先考虑初始相位等于零 ($\phi$= 0) 的波浪的负号。波浪的相位将是 ($kx = \omega t$)。考虑跟踪波浪上的某个点，例如波峰。对于任何 n 的整数值，也就是说$k x-\omega t=n \pi+\frac{\pi}{2}$，何时，波峰都会出现。$\sin(kx - \omega t = 1.00$ 例如，一个特定的波峰出现在$k x-\omega t=\frac{\pi}{2}$。随着波浪的移动，时间会增加，x 也必须增加才能保持相位相等$\frac{\pi}{2}$。因此，负号表示在正 x 方向上移动的波浪。使用加号，$k x+\omega t=\frac{\pi}{2}$。随着时间的增加，x 必须减小才能保持相位等于$\frac{\pi}{2}$。加号用于在负 x 方向上移动的波浪。总而言之，$y(x, t)=A \sin (k x-\omega t+\phi)$对在正 x 方向移动的波浪进行建$y(x, t)=A \sin (k x+\omega t+\phi)$模，对在负 x 方向移动的波浪进行建模。

方程\ ref {16.4} 被称为简单谐波函数。波函数是这样的任何函数$f(x, t)=f(x-v t)$。在本章后面，我们将看到它是线性波动方程的解。请注意，它同样$y(x, t)=A \cos \left(k x+\omega t+\phi^{\prime}\right)$有效，因为它对应于不同的相移$\phi^{\prime}=\phi-\frac{\pi}{2}$。

寻找正弦波的特征

要找出正弦波的振幅、波长、周期和频率，请用表格写下波函数$y(x, t)=A \sin (k x-\omega t+\phi)$。
振幅可以直接从方程中读取，等于$A$。
波的周期可以从角频率中推导出来$ \left(T=\frac{2 \pi}{\omega}\right)$。
频率可以通过以下方式找到$f = \frac{1}{T}$
可以使用波数找到波长$\left(\lambda=\frac{2 \pi}{k}\right)$。

示例$\PageIndex{1}$: Characteristics of a traveling wave on a string

拉紧弦上的横向波浪是使用波浪函数建模的

\[ \begin{align*} y(x, t) &=A \sin (k x-w t) \\[4pt] &= (0.2 \: \mathrm{m}) \sin \left(6.28 \: \mathrm{m}^{-1} x-1.57 \: \mathrm{s}^{-1} t\right) \end{align*} \]

找出波浪的振幅、波长、周期和速度。

策略

波浪的所有这些特征都可以从方程中包含的常数或这些常数的简单组合中找到。

解决方案

1。振幅、波数和角频率可以直接从波动方程中读取：

\ begin {align*}
y (x, t) =& A\ sin (k x-w t) =0.2\:\ mathrm {m}\ sin\ left (6.28\:\ mathrm {m} ^ {-1} t\ 右)\ nonnumber\\\\ left (A=0.2\:\ mathrm {m}; k=6.28\:\ mathrm {m} ^ {-1};\ omega=1.57\:\ mathrm {s} ^ {-1}\ 右)\ nonumber
\ end {align*}

2。波数可用于查找波长：

\ begin {array} {l}
k=\ frac {2\ pi} {
\ lambda}\\\ lambda=\ frac {2\ pi} {k} =\ frac {2\ pi} {6.28\:\ mathrm {m}
\ end {array}

3。使用角频率可以找到波浪周期：

\ begin {array} {l}
\ omega=\ frac {2\ pi} {T}\\
T=\ frac {2\ pi} {\ omega} =\ frac {2\ pi} {1.57\:\ mathrm {s} ^ {-1}} =4\:\ mathrm {s}
\ end {array}

4。使用波数和角频率可以找到波速。波浪的方向可以通过考虑以下符号来确定$k x \mp \omega t$：负号表示波浪正向 x 方向移动：

\[ |v|=\frac{\omega}{k}=\frac{1.57 \: \mathrm{s}^{-1}}{6.28 \: \mathrm{m}^{-1}}=0.25 \: \mathrm{m} / \mathrm{s} \nonumber\]

意义

波浪的所有特征都包含在波函数中。请注意，波速是波浪在与波浪运动平行的方向上的速度。绘制介质 y 与位置 x 的高度两倍 t = 0.00 s 和 t = 0.80 s 可以提供波浪的图形可视化（图$\PageIndex{4}$）。

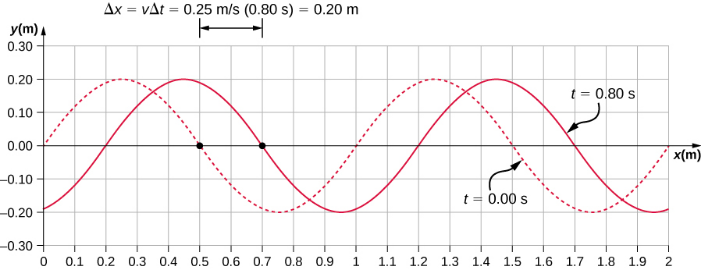
图中显示了两个横向波，其 y 值从 -0.2 m 到 0.2 m 不等。一个标记为 t=0 秒的波浪显示为一条虚线。它在 x 处的波峰等于 0.25 m 和 1.25 m。另一波标记 t=0.8 秒的波峰显示为实线。它在 x 处的波峰等于 0.45 m 和 1.45 m。 — 图$\PageIndex{4}$：波浪 y 的高度与位置 x 的函数关系的图表，用于拍摄两次波浪的快照。虚线表示时间 t = 0.00 s 时的波浪，实线表示 t = 0.80 秒时的波浪。由于波速恒定，因此波浪传播的距离是波速乘以时间间隔。黑点表示用于测量波浪位移的点。介质上下移动，而波浪向右移动。

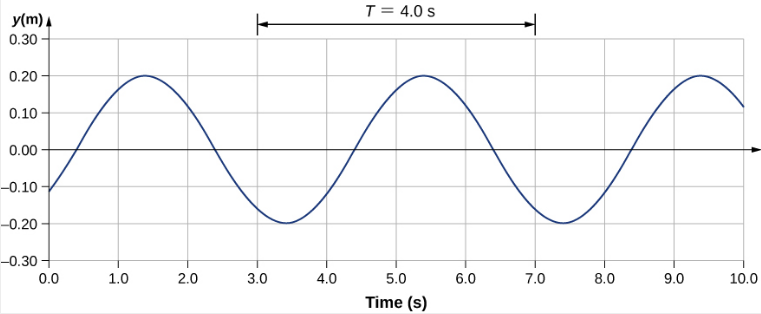
运动还有第二种速度。在此示例中，波浪是横向的，当介质垂直于运动方向上下振荡时，波浪水平移动。图中的图表$\PageIndex{5}$显示了介质在 x = 0.60 m 处的运动随时间的变化。请注意，每隔 4.0 秒，波浪介质在 y = +0.20 m 和 y = −0.20 m 之间上下振荡。

该图显示了图表上的横向波浪。它的 y 值从 -0.2 m 到 0.2 m 不等。x 轴以秒为单位显示时间。波浪的两个相同部分之间的水平距离标记为 T = 4 秒。 — 图$\PageIndex{5}$：波浪高度 y 与时间 t 函数的图表，位置 x = 0.6 m。介质每个周期在 y = +0.20 m 和 y = −0.20 m 之间振荡。所代表的时段在振荡中选出两个方便的点来衡量该时段。可以在振幅和速度相同的任意两个相邻点之间测量周期$(\partial y / \partial t)$。速度可以通过查看 y-vers-t 图上与点相切的斜率来找到。请注意，在 t = 3.00 s 和 t = 7.00 秒时，高度和速度相同，振荡周期为 4.00 秒。

练习$\PageIndex{1}$

上面的波函数是使用正弦函数得出的。可以改用余弦函数吗？

介质的速度和加速度

如示例所示$\PageIndex{2}$，波速是恒定的，表示波浪在介质中传播时的速度，而不是构成介质的粒子的速度。当波浪在介质中传播时，介质的粒子围绕平衡位置振荡。如果横波在 x 方向传播，则粒子在 y 方向上下振荡，垂直于波浪的运动。介质中粒子的速度不是恒定的，这意味着存在加速度。介质的速度垂直于横波中的波速，可以通过取位置方程相对于时间的偏导数来得出。偏导数是通过取函数的导数来找到的，将所有变量视为常量，所讨论的变量除外。对于相对于时间的偏导数$t$，位置$x$被视为常数。尽管如果你以前没看过，这听起来可能很奇怪，但本练习的目的是找到某个点的横向速度，所以从这个意义上讲，$x$-position 没有改变。我们有

\[\begin{split} y(x,t) & = A \sin (kx - \omega t + \phi) \\ v_{y} (x,t) & = \frac{\partial y(x,t)}{\partial t} = \frac{\partial}{\partial t} [A \sin (kx - \omega t + \phi)] \\ & = -A \omega \cos (kx - \omega t + \phi) \\ & = -v_{y\; max} \cos (kx - \omega t + \phi) \ldotp \end{split}\]

介质最大速度的大小为$|v_{y\, max}| = A \omega$。从振荡和弹簧上的质量来看，这可能看起来很熟悉。

我们可以通过取速度方程相对于时间的偏导数来找到介质的加速度，

\[\begin{split} a_{y} (x,t) & = \frac{\partial v_{y}(x,t)}{\partial t} = \frac{\partial}{\partial t} [-A \omega \cos (kx - \omega t + \phi)] \\ & = -A \omega^{2} \sin (kx - \omega t + \phi) \\ & = -a_{y\; max} \sin (kx - \omega t + \phi) \ldotp \end{split}\]

最大加速度的大小为 |a _{y max} | = A$\omega^{2}$。介质的粒子或质量元素在机械波的简单谐波运动中振荡。

线性波动方程

我们刚刚通过取位置 y 的偏导数来确定介质在 x 位置的速度。对于横向波，该速度垂直于波的传播方向。我们通过取速度相对于时间的偏导数得出加速度，这是位置的二阶时间导数：

\[a_{y} (x,t) = \frac{\partial^{2} y(x,t)}{\partial t^{2}} = \frac{\partial^{2}}{\partial t^{2}} [A \sin(kx - \omega t + \phi)] = -A \omega^{2} \sin (kx - \omega t + \phi) \ldotp\]

现在考虑相对于另一个变量，即保持时间常数的位置 x 的偏导数。一阶导数是波在时间 t 处的点 x 处的斜率，

\[slope = \frac{\partial y(x,t)}{\partial x} = \frac{\partial}{\partial x} [A \sin (kx - \omega t + \phi)] = Ak \cos (kx - \omega t + \phi) \ldotp\]

二阶偏导数表示波浪斜率相对于位置的变化——换句话说，波浪的曲率，其中

\[curvature = \frac{\partial^{2} y(x,t)}{\partial x^{2}} = \frac{\partial^{2}}{\partial x^{2}} [A \sin (kx - \omega t + \phi)] = -Ak^{2} \sin (kx - \omega t + \phi) \ldotp\]

加速度和曲率之比导致了物理学中一种非常重要的关系，称为线性波动方程。取比率并使用方程 v =$\frac{\omega}{k}$ 得出线性波动方程（也简称为波动方程或振动串方程），

\[\begin{split} \frac{\frac{\partial^{2} y(x,t)}{\partial t^{2}}}{\frac{\partial^{2} y(x,t)}{\partial x^{2}}} & = \frac{-A \omega^{2} \sin (kx - \omega t + \phi)}{-Ak^{2} \sin (kx - \omega t + \phi)} \\ & = \frac{\omega^{2}}{k^{2}} = v^{2}, \end{split}\]

\[\frac{\partial^{2} y(x,t)}{\partial x^{2}} = \frac{1}{v^{2}} \frac{\partial^{2} y(x,t)}{\partial t^{2}} \ldotp \label{16.6}\]

方程\ ref {16.6} 是线性波动方程，它是物理学和工程学中最重要的方程之一。我们在这里得出的是横向波，但在研究纵波时它同样重要。这种关系也是使用正弦波得出的，但它成功地描述了形式为 y (x, t) = f (x vt) 的任何波浪或脉冲。这些波浪是由于介质的线性恢复力而产生的，因此被称为线性波动方程。任何满足此方程的波函数都是线性波函数。

线性波动方程的一个有趣方面是，如果两个波函数是线性波动方程的单独解，那么两个线性波函数的总和也是波动方程的解。假设两个横向波沿 x 轴传播，占据相同的介质。假设单个波浪可以使用波函数 y ₁ (x, t) = f (x vt) 和 y ₂ (x, t) = g (x vt) 进行建模，它们是线性波动方程的解，因此是线性波函数。波函数的总和就是波浪函数

\[y_{1} (x,t) + y_{2} (x,t) = f(x \mp vt) + g(x \mp vt) \ldotp\]

以线性波动方程为例：

\[\begin{split} \frac{\partial^{2} (f + g)}{\partial x^{2}} & = \frac{1}{v^{2}} \frac{\partial^{2} (f + g)}{\partial t^{2}} \\ \frac{\partial^{2} f}{\partial x^{2}} + \frac{\partial^{2} g}{\partial x^{2}} & = \frac{1}{v^{2}} \left(\dfrac{\partial^{2} f}{\partial t^{2}} + \frac{\partial^{2} g}{\partial t^{2}}\right) \ldotp \end{split}\]

这表明，如果以代数方式添加两个线性波函数，则生成的波函数也是线性的。此波函数对生成波浪的介质在 x 轴上每个位置的位移进行建模。如果两个线性波占据相同的介质，则据说它们会干扰。如果可以使用线性波函数对这些波浪进行建模，则这些波函数将形成由单个波浪干扰产生的波浪方程。介质在生成的波浪的每个点的位移是单个波浪引起的位移的代数和。

更进一步，如果波函数 y1 (x, t) = f (x vt) 和 y2 (x, t) = g (x vt) 是线性波动方程的解，那么 Ay ₁ (x, t) + By ₂ (x, y)（其中 A 和 B 是常数）也是线性波动方程的解。这个属性被称为叠加原理。干扰和叠加在《波浪干扰》中有更详细的介绍。

示例$\PageIndex{2}$: Interference of Waves on a String

假设一根由两个学生拉紧的很长的绳子，两端各一个。学生 A 振荡弦的末端，产生一个使用波函数 y ₁ (x, t) = A sin (kx −$\omega$ t) 建模的波浪，学生 B 振荡琴弦以两倍的频率产生，朝相反的方向移动。两个波浪以相同的速度移动 v =$\frac{\omega}{k}$。这两个波浪相互干扰，形成波浪函数为 y _R (x, t) = y ₁ (x, t) + y ₂ (x, t)。使用线性波动方程求出生成的波浪的速度$\frac{\partial^{2} y(x,t)}{\partial x^{2}} = \frac{1}{v^{2}} \frac{\partial^{2} y(x,t)}{\partial t^{2}}$。

策略

首先，为第二个学生创建的波浪写波函数。请注意，第二波的角频率是第一波频率的两倍（2$\omega$），并且由于两个波浪的速度相同，因此第二波的波数是第一波的两倍（2k）。接下来，为生成的波函数写出波动方程，即两个独立波函数的总和。然后找到相对于位置的第二个偏导数和相对于时间的第二个偏导数。使用线性波动方程求出所生成波浪的速度。

解决方案

写下第二波的波函数：y ₂ (x, t) = A sin (2kx + 2$\omega$ t)。
写下生成的波浪函数：$$y_ {R} (x, t) = y_ {1} (x, t) + y (x, t) = A\ sin (kx-\ omega t) + A\ sin (2kx + 2\ omega t)\ ldotp$$
找到偏导数：$$\ begin {split}\ frac {\ partial y_ {R} (x, t)} {\ partial x} & =-Ak\ cos (kx-\ omega t) + 2Ak\ cos (2kx + 2\ omega t)，\\\ frac {\ partial^ {2} y_ {R} (x, t)} {\ partial x^ {2}} & =-Ak^ {2}\ sin (kx-\ omega t) -4Ak^ {2}\ sin (2kx + 2\ omega t)，\\\ frac {\ partial y_ {R} (x, t)} {\ partial t}& =-A\ omega\ cos (kx-\ omega t) + 2A\ omega\ cos (2kx + 2\ omega t)，\\\ frac {\ partial^ {2} y_ {R} (x, t)} {\ partial t^ {2}\ sin (kx-\ omega t)-4A\ omega^ {2}\ sin (2kx + 2\ omega t)\ ldotp\ end {split} $$
使用波动方程求出生成的波浪的速度：$$\ begin {split}\ frac {\ partial^ {2} y (x, t)} {\ partial x^ {2}} {\ partial t^ {2}} {\ partial t^ {2}}，\\-Ak^ {2}\ sin (kx-\ omega t) + 4Ak^ {2}\ sin (2kx + 2\ omega t) & =\ frac {1} {v^ {2}}\ 左 (-A\ omega^ {2}\ sin (kx-\\omega t) -4A\ omega^ {2}\ sin（2kx + 2\ omega t）\ 右），\\ k^ {2}\ 左（-A\ sin（kx-\ omega t）+ 4A\ sin（2kx + 2\ omega^ {2}} {v^ {2}}\ 左（-A\ sin (kx-\ omega t) -4A\ sin (2kx + 2\ omega t)\ 右)，\\ k^ {2} & =\ frac {\ omega^ {2}} {v^ {2}}，\\ |v| & =\ frac {\ omega} {k}\ ldotp\end {split} $$

意义

生成的波浪的速度等于原始波浪的速度$\left(v = \frac{\omega}{k}\right)$。我们将在下一节中说明，弦上简单谐波的速度取决于弦中的张力和琴弦每长度的质量。出于这个原因，分量波以及由此产生的波都以相同的速度传播也就不足为奇了。

练习 16.4

波动方程$\frac{\partial^{2} y(x,t)}{\partial x^{2}} = \frac{1}{v^{2}} \frac{\partial^{2} y(x,t)}{\partial t^{2}}$适用于任何形式为 y (x, t) = f (x vt) 的波浪。在上一节中，我们说过余弦函数也可以用于对简单的谐波机械波进行建模。检查波浪是否

\[y(x,t) = (0.50\; m) \cos (0.20 \pi\; m^{-1} x - 4.00 \pi s^{-1} t + \frac{\pi}{10})\]

是波动方程的解。

任何符合波动方程的干扰都可以作为沿着 x 轴移动的波浪传播，波速为 v。它同样适用于弦上的波浪、声波和电磁波。这个方程非常有用。例如，它可以用来显示电磁波以光速移动。

寻找正弦波的特征

示例\(\PageIndex{1}\): Characteristics of a traveling wave on a string

解决方案

练习\(\PageIndex{1}\)

示例\(\PageIndex{2}\): Interference of Waves on a String

解决方案

练习 16.4