16.2: 旅行浪潮

Last updated
Save as PDF

Page ID: 204295

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

描述波浪运动的基本特征
定义波长、振幅、周期、频率和波速等术语
解释纵波和横波之间的区别，并举例说明每种类型
列出不同类型的波浪

我们在《振荡》中看到，振荡运动是一种重要的行为类型，可用于模拟各种物理现象。振荡运动也很重要，因为振荡可以产生波浪，而波浪在物理学中至关重要。我们在振荡一章中研究的许多术语和方程同样适用于波浪运动（图$\PageIndex{1}$）。

海浪的照片。 — 图$\PageIndex{1}$：当你听到 “波浪” 这个词时，想到的第一张照片可能是海浪。尽管这种破浪以及一般的海浪与我们将要讨论的基本波浪特征有明显的相似之处，但驱动海浪的机制非常复杂，超出了本章的范围。将本章中的概念应用于海浪似乎很自然，甚至是有利的，但是海浪是非线性的，本章中介绍的简单模型并不能完全解释它们。（来源：史蒂夫·尤尔维森）

波浪的类型

波浪是一种从其产生的地方传播或移动的干扰。波有三种基本类型：机械波、电磁波和物质波。

基本机械波受牛顿定律支配，需要介质。介质是机械波传播的物质，介质在变形时会产生弹性恢复力。机械波传递能量和动量，而不传递质量。机械波的一些例子是水波、声波和地震波。水波的介质是水；对于声波，介质通常是空气。（声波也可以在其他媒体中传播；我们将在 S ound 中对此进行更详细的介绍。）对于地表水浪，干扰发生在水面，可能是由向池塘投掷的石头或游泳者反复飞溅水面造成的。对于声波来说，干扰是气压的变化，可能是由扬声器内部的振荡锥或振动音叉造成的。在这两种情况下，干扰都是流体分子的振荡。在机械波中，能量和动量随着波浪的运动而传递，而质量则围绕平衡点振荡。（我们在《波浪的能量与力量》中讨论了这个问题。）地震通过几种类型的扰动产生地震波，包括对地球表面的干扰和地表下的压力扰动。地震波穿过形成地球的固体和液体。在本章中，我们将重点介绍机械波。

电磁波与电场和磁场中的振荡有关，不需要介质。示例包括伽玛射线、X 射线、紫外线、可见光、红外波、微波和无线电波。电磁波可以以光速穿过真空，v = c = 2.99792458 x 10 ⁸ m/s。例如，来自遥远恒星的光在太空真空中传播并到达地球。电磁波具有一些与机械波相似的特征；电磁波中有更详细的介绍。

物质波是被称为量子力学的物理学分支的核心部分。这些波与自然界中发现的质子、电子、中子和其他基本粒子有关。所有类型的物质都具有波浪状特性的理论最早是由路易斯·德·布罗格利在1924年提出的。在 “光子” 和 “物质波” 中讨论了物质波。

机械波

机械波表现出所有波浪的共同特征，例如振幅、波长、周期、频率和能量。所有波浪特征都可以通过一小部分基本原理来描述。

最简单的机械波会重复几个周期，并且与简单的谐波运动有关。这些简单的谐波可以使用正弦和余弦函数的某种组合进行建模。例如，假设在水面上移动的简化地表水波，如图所示$\PageIndex{2}$。与复杂的海浪不同，在地表水波中，介质（在本例中为水）垂直移动，上下摆动，而波浪的干扰在介质中水平移动。在图中$\PageIndex{2}$，当波峰和波谷（峰值和低谷）经过鸟的下方时，海浪使海鸥以简单的谐波运动上下移动。波峰是波浪的最高点，低谷是波浪的最低部分。上下运动一次完全振荡的时间是波浪的周期 T。波浪的频率是单位时间内通过一个点的波浪数，等于 f =$\frac{1}{T}$。周期可以使用任何方便的时间单位来表示，但通常以秒为单位来衡量；频率通常以赫兹 (Hz) 来测量，其中 1 Hz = 1 s ⁻¹。

波长的长度称为波长，由希腊字母 lambda ($\lambda$) 表示，它以任何方便的长度单位（例如厘米或米）进行测量。可以在介质上具有相同高度和相同斜率的任意两个相似点之间测量波长。在图中$\PageIndex{2}$，波长显示了在两个波峰之间测量的波长。如上所述，波浪的周期等于一次振荡的时间，但它也等于一个波长穿过波浪路径上某个点的时间。

波浪的振幅 (A) 是衡量介质相对于其平衡位置的最大位移的量度。在图中，平衡位置由虚线表示，如果没有波浪流过虚线，虚线是水的高度。在这种情况下，波浪是对称的，波峰比平衡位置高出一点距离 +A，波谷比平衡位置低一段距离 −A。振幅的单位可以是厘米或米，也可以是任何方便的距离单位。

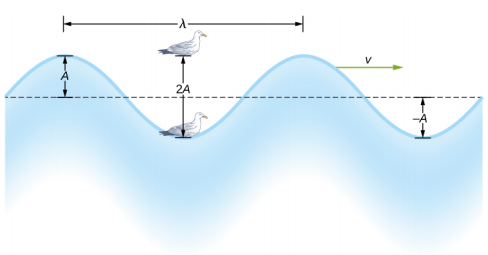
图中显示了以水平线标示平衡位置的波浪。从直线到波峰的垂直距离标记为 x，从直线到波谷的垂直距离标记为负 x。图中有一只鸟在波浪中上下摆动。鸟类行进的垂直距离标记为 2 倍。两个连续波峰之间的水平距离被标记为 lambda。指向右侧的向量被标记为 v 下标 w。 — 图$\PageIndex{2}$：理想化的地表水浪经过海鸥下方，海鸥以简单的谐波运动上下摆动。波长为波长$\lambda$，即波浪的相邻相同部分之间的距离。波浪的振幅 A 是波浪相对于平衡位置的最大位移，由虚线表示。在本示例中，介质上下移动，而表面的干扰以 v 的速度平行于表面传播。

图中的水波以传播速度在介质中移动$\vec{v}$。波速的大小是波浪在给定时间内传播的距离，即一个周期内的一个波长，波速是波速的大小。在方程形式中，这是

\[v = \frac{\lambda}{T} = \lambda f \ldotp \label{16.1}\]

这种基本关系适用于所有类型的波浪。对于水波，v 是表面波的速度；对于声音，v 是声速；对于可见光，v 是光速。

横波和纵波

我们已经看到，简单的机械波由周期性的干扰组成，它通过介质从一个地方传播到另一个地方。在图$\PageIndex{3}$ (a) 中，波浪沿水平方向传播，而介质在垂直方向受到干扰。这样的波浪被称为横向波。在横向波中，波浪可以向任何方向传播，但介质的干扰垂直于传播方向。相比之下，在纵波或压缩波中，扰动平行于传播方向。图$\PageIndex{3}$ (b) 显示了纵波的示例。扰动的大小是其振幅 A，与传播速度 v 完全无关。

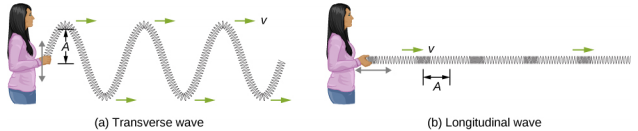
标有 “横波” 的图 a 显示了一个人握住水平放置的长弹簧的一端，然后上下移动。弹簧形成波浪，从人身上传播开来。这被标记为横波。波峰与弹簧平衡位置之间的垂直距离标为 A。图 b 标有纵波，显示了水平来回移动弹簧的人。弹簧被压缩并交替拉长。这被标记为纵波。从一次压缩的中间到一次稀有度中间的水平距离标记为 A。 — 图$\PageIndex{3}$：(a) 在横波中，介质垂直于波速振荡。在这里，弹簧垂直上下移动，而波浪向右水平传播。 (b) 在纵波中，介质与波浪的传播平行振荡。在这种情况下，弹簧来回振荡，而波浪向右传播。

图 (b) 所示弹簧部分的简单图形表示如图$\PageIndex{3}$ (b) 所示$\PageIndex{4}$。图$\PageIndex{4}$ (a) 显示了弹簧在任何波浪向下移动之前的平衡位置。弹簧上的一个点用蓝点标记。图$\PageIndex{4}$ (b) 至 (g) 显示了相隔四分之一周期拍摄的弹簧的快照，在弹簧结束后的某个时候，弹簧以恒定的频率在 x 方向上来回振荡。波浪的干扰被视为弹簧的压缩和膨胀。请注意，当纵波以恒定速度沿正 x 方向移动时，蓝点围绕其平衡位置振荡距离为 A。距离 A 是波浪的振幅。当波浪穿过弹簧时，点的 y 位置不会改变。波浪的波长在 (d) 部分中测量。波长取决于波速和驱动力的频率。

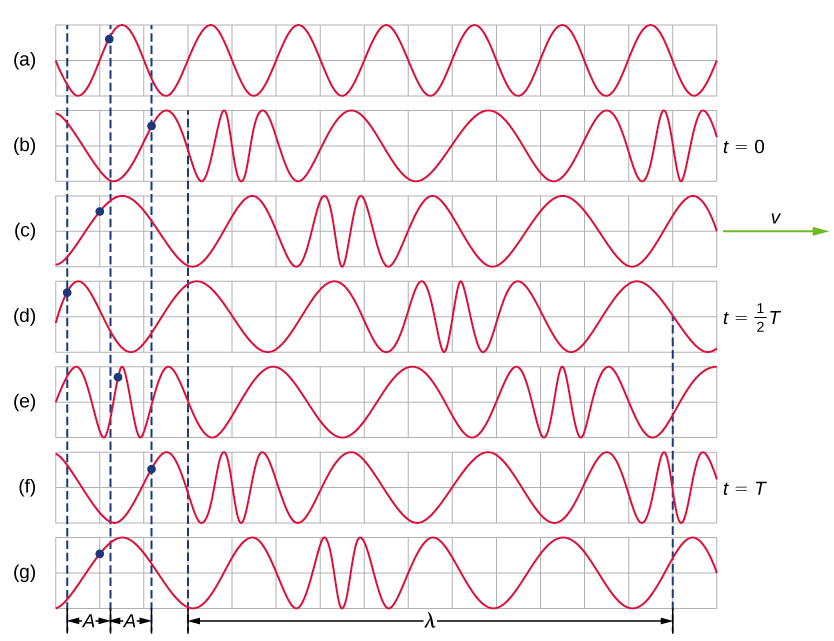
图 a 到 g 显示了纵波穿过弹簧的不同阶段。一个蓝点标记弹簧上的一个点。当波浪向右传播时，它从左向右移动。在图 b 中，时间 t=0 时，点在均衡位置的右边。在图 d 中，时间 t 等于一半 T 时，点在平衡位置的左边。在图 f 中，时间 t=t 时，点再次向右。平衡位置与点的最左或最右位置之间的距离相同，标记为 A。波浪的两个相同部分之间的距离被标记为 lambda。 — 图$\PageIndex{4}$：（a）这是图$\PageIndex{3}$（b）所示的拉伸弹簧部分的简单图形表示，代表弹簧在弹簧上产生任何波浪之前的平衡位置。弹簧上的一个点用蓝点标记。 (b—g) 纵向波是通过沿 x 轴来回摆动弹簧末端（未显示）而产生的。带波长的纵波以 +x 方向沿弹簧移动$\lambda$，波速为 v。为方便起见，波长以 (d) 来测量。请注意，弹簧上标有蓝点的点在距离平衡位置 A 处来回移动，围绕该点的平衡位置振荡。

波浪可以是横向的、纵向的，也可以是两者的组合。横向波的例子是弦乐器上的波浪或水上的表面波，例如在池塘上移动的波浪。空气和水中的声波是纵向的。对于声波来说，干扰是流体中传递的压力的周期性变化。流体没有明显的剪切强度，因此，其中的声波是纵波。固体中的声音可以具有纵向和横向分量，例如地震波中的声音。地震在地球表面下产生具有纵向和横向分量的地震波（分别称为压缩波或 P 波以及剪切波或 S 波）。地震波的组成部分具有重要的个体特征——例如，它们以不同的速度传播。地震的地表波也类似于水面上的地表波。海浪也有横向和纵向两个部分。

示例 16.1：在字符串上挥动

在物理实验室里，一名学生拿起一根 30.00 米长的绳子，将一端固定在墙上。然后，学生握住绳子的自由端，保持绳索中的张力恒定。然后，学生开始以 2.00 Hz 的频率向上和向下移动弦的末端，沿着弦向下发送波浪。琴弦末端的最大位移量为 20.00 cm。第一波在创建 6.00 秒后冲击实验室墙。 (a) 波浪的速度是多少？ (b) 浪潮的周期是多少？ (c) 波长的波长是多少？

策略

波浪的速度可以通过将行进的距离除以时间来得出。
波浪周期与驱动力频率相反。
波长可以从速度和周期 v = 中找到$\frac{\lambda}{T}$。

解决方案

第一波浪在 6.00 秒内传播了 30.00 米：$$v =\ frac {30.00\; m} {6.00\; s} = 5.00\; m/s\ ldotp$$
。周期等于频率的逆数：$$T =\ frac {1} {f} =\ frac {1} {2.00\; s^ {-1}} = 0.50\; s\ ldotp$$
波长等于速度乘以周期：$$\ lambda = vT = (5.00\; m/s) (0.50\; s) = 2.50\; m\ ldotp$$

意义

振荡驱动力产生的波的频率等于驱动力的频率。

练习 16.1

g 弹出吉他弦时，由于波浪在琴弦中移动，吉他弦会振荡。琴弦的振动导致空气分子振荡，形成声波。声波的频率等于振动弦的频率。声波的波长是否总是等于弦上波浪的波长？

示例 16.2：波浪的特征

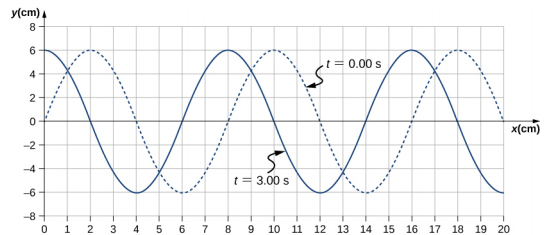
横向机械波以恒定的波速沿正 x 方向通过弹簧（如图$\PageIndex{3}$ (a) 所示）传播，介质围绕平衡位置在 +A 和 −A 之间振荡。图中的图表$\PageIndex{5}$显示了弹簧 (y) 的高度与位置 (x) 的关系，其中 x 轴指向传播方向。该图以虚线显示弹簧高度与 t = 0.00 s 处的 x 位置的对比，t = 3.00 s 处的波浪显示为实线。 (a) 确定波长的波长和振幅。 (b) 找出波浪的传播速度。 (c) 计算波浪的周期和频率。

图中显示了两个横向波，其 y 值从 -6 cm 到 6 cm 不等。标记为 t=0 秒的波浪显示为虚线。它在 x 处的波峰等于 2、10 和 18 厘米。另一个标有 t=3 秒的波浪显示为实线。它在 x 处的波峰等于 0、8 和 16 厘米。 — 图$\PageIndex{5}$：在两个时刻显示的横向波。

策略

振幅和波长可以从图表中确定。
由于速度是恒定的，因此波浪的速度可以通过将波浪行进的距离除以波浪传播距离所花费的时间来得出。
周期可以从 v = 中找到$\frac{\lambda}{T}$，频率可以从 f = 中找到$\frac{1}{T}$。

解决方案

读取图中的波长，看图中的紫色箭头$\PageIndex{6}$。看绿色箭头读取振幅。波长为$\lambda$ 8.00 厘米，振幅为 A = 6.00 厘米。

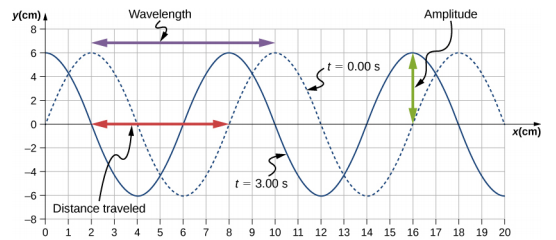
图中显示了两个横向波，其 y 值从 -6 cm 到 6 cm 不等。标记为 t=0 秒的波浪显示为虚线。它在 x 处的波峰等于 2、10 和 18 厘米。另一个标有 t=3 秒的波浪显示为实线。它在 x 处的波峰等于 0、8 和 16 厘米。两个连续波峰之间的水平距离被标记为波长。这是从 x=2 厘米到 x=10 厘米不等。从平衡位置到波峰的垂直距离被标记为振幅。这是从 y=0 厘米到 y=6 厘米不等。红色箭头标有行驶距离。这是从 x=2 厘米到 x=8 厘米不等。 — 图$\PageIndex{6}$：波浪的位移图上标出的波浪特征。

波浪从时间 t = 0.00 s 到时间 t = 3.00 s 的传播距离可以在图中看出。以红色箭头为例，它显示了波峰在 3 秒内移动的距离。距离为 8.00 cm − 2.00 cm = 6.00 cm。速度为 $$v =\ frac {\ Delta x} {\ Delta t} =\ frac {8.00\; cm-2.00\; cm} {3.00\; s-0.00\; s} = 2.00\; cm/s\ ldotp$$
周期为 T =$\frac{\lambda}{v}$$\frac{8.00\; cm}{2.00\; cm/s}$ = 4.00\; s，频率为 f =$\frac{1}{T}$$\frac{1}{4.00\; s}$ = 0.25 Hz。

意义

请注意，波长可以使用任意两个连续重复的相同点来找到，它们具有相同的高度和斜率。你应该选择两个最方便的点。也可以使用任何方便的点找到位移。

练习 16.2

当波浪干扰在介质中移动时，横向或纵向机械波的传播速度可能是恒定的。以横向机械波为例：介质的速度是否也恒定？