Skip to main content
Global

14.E：流体力学（练习）

  1. Last updated
  2. Save as PDF
  • Page ID
    205057

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    概念性问题

    14.1 流体、密度和压力

    1. 以下哪些物质是室温和大气压下的液体：空气、汞、水、玻璃？
    2. 为什么气体比液体和固体更容易压缩？
    3. 解释空气密度如何随海拔变化而变化。
    4. 该图显示了一杯装满边缘的冰水。 冰融化后水会溢出吗？ 解释你的答案。

    一张装满边缘的一杯冰水的照片。

    1. 压力与刀的锋利度及其切割能力有何关系？
    2. 为什么静态流体在表面上施加的力总是垂直于表面？
    3. 想象一下，在靠近北极的偏远地区，一块冰漂浮在湖中。 在湖边，陆地上有一座体积与浮冰相同体积的冰川。 如果两块冰都因为全球气温上升而融化，融化的冰全部进入湖中，那么哪一个会导致湖泊水位上升得最大？ 解释一下。
    4. 在芭蕾舞中，脚尖跳舞（在脚尖上）比普通的跳舞或走路要难得多。 从压力的角度解释原因。
    5. 当你躺在沙滩上晒日光浴时，大气压力会对你的身体顶部施加很大的力（相当于身体上方大气的重量——大约 10 吨）。 你为什么能起床？
    6. 为什么大气压的下降速度比与海拔线性下降的速度更快？
    7. 该图显示了在河堤外泄漏处放置的沙袋如何有效地阻止堤下的水流。 解释一下沙袋柱内的少量水如何能够平衡堤后面更大的水域。

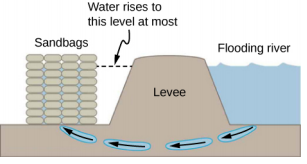
    在河堤外漏水处放置沙袋的示意图。 一堆沙袋的高度与堤坝的高度相同，超过了洪水河流中的最大水位。

    1. 由于大气压力，大坝上有净力吗？ 解释你的答案。
    2. 大气压会增加硬质储罐中的气体压力吗？ 在玩具气球里？ 一般来说，什么时候大气压不影响流体中的总压力？
    3. 你可以用拳头将软木塞打入一个坚固的葡萄酒瓶中，但是软木塞必须直接压在装满瓶子的液体上，软木塞和液体之间不能有空气。 解释为什么只有在软木塞和液体之间没有空气的情况下瓶子才会破裂。

    14.2 测量压力

    1. 解释为什么压力计两侧都向大气开放，即使管道的直径不同，液体在压力计两侧都达到相等的水平。

    14.3 帕斯卡原理和液压系统

    1. 假设液压系统中的主缸高度大于它所控制的气缸的高度。 解释这将如何影响正在控制的气缸上产生的力。

    14.4 阿基米德原理和浮力

    1. 拔掉装满的浴缸的插头比空的浴缸需要更大的力量。 这与阿基米德的原则相矛盾吗？ 解释你的答案。
    2. 在 “失重” 的环境中，例如在航天飞机中，液体会施加浮力吗？ 解释你的答案。
    3. 同一艘船在盐水中的漂浮量会比在淡水中漂浮得更高吗？ 解释你的答案。
    4. 弹珠掉入了部分填充的浴缸水槽底部。 它们的一部分重量由浮力支撑，但浴缸底部的向下力恰好随着弹珠的重量而增加。 解释原因。

    14.5 流体动力学

    1. 文本中的许多数字都显示了流线型。 解释为什么流线最接近的地方流体速度最快。 （提示：考虑流体速度和流体流经的横截面积之间的关系。）

    14.6 伯努利方程

    1. 你可以用拇指部分遮住花园水管的开口，这样可以更远的距离喷水。 解释这是如何工作的。
    2. 在装饰性喷泉中，水几乎垂直向上射出，观察到溪流随着上升而扩大。 相反，直接从水龙头掉下来的水流会变窄。 解释原因。
    3. 回头看图 14.29。 回答以下两个问题。 为什么 p o 小于大气层？ 为什么 p o 大于 p i？
    4. 为增强夹带而设计的具有窄段的管道称为文丘里管，如下所示。 文丘里在化油器和吸气器中非常常用。 这种结构如何增强夹带？

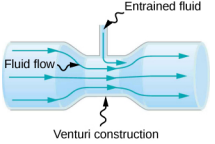
    该图是一张标有风险建设的狭窄管段的管道图。 额外的小型连接是在收缩时进行的，允许夹带的流体进入流体流动。

    1. 有些烟囱管为 T 形，顶部有一个横梁，只要有微风，就能帮助吸收气体。 根据伯努利原理解释这是如何工作的。
    2. 夹带装置可以将液体提升到的高度有限制吗？ 解释你的答案。
    3. 为什么飞机最好在风中起飞而不是随风起飞？
    4. 在热带气旋期间，屋顶有时会被垂直推开，建筑物在受到龙卷风袭击时有时会向外爆炸。 使用伯努利原理来解释这些现象。
    5. 当快速行驶的通勤列车经过时，站在铁轨附近是危险的。 解释为什么大气压力会将你推向行驶中的火车。
    6. 由于伯努利效应，软管喷嘴内的水压可能低于大气压力。 用能量解释水如何在相反的大气压下从喷嘴中冒出来。
    7. 大卫在高速公路上行驶时从车窗滚下来。 地板上一个空的塑料袋迅速飞出了窗外。 解释原因。
    8. 根据伯努利方程，流体中有哪三种能量形式？ （请注意，这些形式是保守的，与伯努利方程中未包括的传热和其他耗散形式不同。）
    9. 下图所示的旧橡胶靴有两个漏洞。 从 Leak 1 喷出的水最大高度可以达到多少？ 从 Leak 2 流出的水的速度与 Leak 1 流出的水的速度有何不同？ 用能量解释你的反应

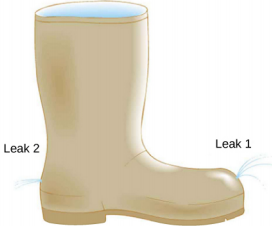
    该图是一张靴子的图，靴子上有两个漏水位于相同的高度。 泄漏 1 点向上，水平泄漏两点。

    1. 由于伯努利效应，软管喷嘴内的水压可能低于大气压力。 用能量解释水如何在相反的大气压下从喷嘴中冒出来。

    14.7 粘度和湍流

    1. 解释为什么液体的粘度会随着温度而降低，也就是说，温度的升高如何减少液体中内聚力的影响？ 还要解释为什么气体的粘度会随着温度的增加而增加，也就是说，气体温度的升高如何在原子和分子之间造成更多的碰撞？
    2. 在上游划独木舟时，最明智的做法是尽可能靠近海岸行驶。 在下游划独木舟时，通常最好待在中间附近。 解释原因。
    3. 管道通常包括水龙头附近的充气管（见下图）。 解释为什么需要它们以及它们是如何工作的。
    4. 多普勒超声波可用于测量体内血液的速度。 如果动脉部分收缩，你预计哪个地方的血速最快：在收缩时或收缩之后？ 收缩时阻力较高的两个不同原因是什么？
    5. 水槽排水管通常有如下所示的设备来帮助加快水的流动。 这是如何工作的？

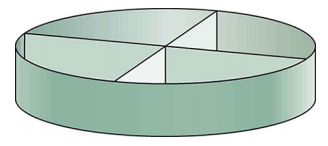
    该图是将水对齐成溪流的设备的示意图。 设备呈圆形，分为四个部分。

    问题

    14.1 流体、密度和压力

    1. 黄金按金衡盎司（31.103 克）出售。 1 金衡盎司纯金的体积是多少？
    2. 汞通常装在装有 34.5 千克（约 76 磅）的烧瓶中。 这么多汞的体积是多少（以升为单位）？
    3. 深呼吸体积为 2.00 L 的空气质量是多少？ 讨论这样的呼吸对身体体积和密度的影响。
    4. 找到物体密度的一种简单方法是测量其质量，然后将其浸入刻度圆柱体中来测量其体积。 取代 89.0 cm 3 水的 240 克岩石的密度是多少？ （请注意，与基于阿基米德原理的其他各种技术相比，这种技术的准确性和实际应用更为有限。）
    5. 假设你的咖啡杯横截面为圆形，侧面为垂直（半径均匀）。 如果装满深度为 7.50 厘米时可容纳 375 克咖啡，它的内部半径是多少？ 假设咖啡的密度与水相同。
    6. 矩形汽油箱装满后可容纳 50.0 kg 汽油。 (a) 如果坦克宽 0.500 米 x 长 0.900 米，它的深度是多少？ (b) 讨论这个油箱的容量是否合理，可以容纳乘用车。
    7. 垃圾压缩机可以将其内容压缩到原始体积的0.350倍。 忽略排出的空气质量，垃圾密度因什么因素而增加？
    8. 2.50 千克的钢质汽油装满后可容纳 20.0 升的汽油。 考虑到钢和汽油所占的体积，满气罐的平均密度是多少？
    9. 由18份金、5份银和1份铜混合而成的18.0克拉金的密度是多少？ （这些值是按质量计算的零件，而不是体积。） 假设这是一种简单的混合物，其平均密度等于其成分的加权密度。
    10. 钉尖在被锤子击中时会施加巨大的压力，因为它会在很小的区域上施加很大的力。 必须对直径为 1.00 毫米的圆形指甲施加什么力才能产生 3.00 x 10 9 N/m 2 的压力？ （这种高压是可能的，因为击中钉子的锤子会在这么短的距离内停下来。）
    11. 玻璃管含有汞。 产生等于 1.00 atm 压力的汞柱的高度会是多少？
    12. 地球上最大的海洋深度位于菲律宾附近的马里亚纳海沟。 假设海沟的深度为 11.0 km，并假设海水的密度一直保持不变，计算该海沟底部的海洋所产生的压力。
    13. 验证 h\(\rho\) g 的 SI 单位是否为 N/m 2。
    14. 如果油箱宽 0.500 米，长 0.900 米，装满后可容纳 50.0 千克汽油，其底部会施加什么压力？
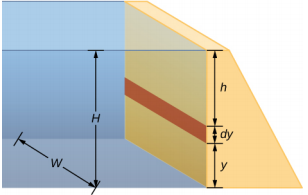
    15. 大坝用来阻挡河流。 大坝的高度 H = 12 m，宽度 W = 10 m。假设水的密度\(\rho\)为 1000 kg/m 3。 (a) 确定大坝的净力。 (b) 为什么大坝的厚度会随着深度的增加而增加？

    该图是用来阻挡河流的高度为 H、宽 w 的大坝的示意图。 标有 dy 的该死的区域位于距大坝底部的 y 高度，位于水位以下 h 的高度。

    14.2 测量压力

    1. 假设与气球相连的压力计使用水，而与气球罐相连的压力计含有汞，则找出图 14.12 所示的气球和花生罐中的压力表和绝对压力。 以气球的水厘米为单位表示，罐子的水以毫米为单位表示，每个 h = 0.0500 米。
    2. 装满水的压力计必须有多高才能测量高达 300 mm Hg 的血压？
    3. 假设自行车轮胎非常灵活，仅靠压力就能支撑自行车和骑手的重量，那么如果自行车和骑手的总重量为 80.0 kg，轮胎中的表压为 3.50 x 10 5 Pa，则计算轮胎与地面接触的总面积。

    14.3 帕斯卡原理和液压系统

    1. 示例 14.3 中考虑的液压系统中传递的压力是多少？ 在大气中表达你的答案。
    2. 必须对液压升降机的主缸施加什么力才能支撑停在第二个气缸上的2000千克汽车（大型汽车）的重量？ 主缸的直径为 2.00 厘米，第二个气缸的直径为 24.0 厘米。
    3. 派对结束后，主持人将几瓶葡萄酒的残余物倒入水罐中。 然后，主人将直径为2.00厘米的软木塞插入瓶中，使其与葡萄酒直接接触。 当主人将软木塞压到位，水罐的底部（直径为14.0厘米）脱落时，主持人感到惊讶。 计算他用 120-N 的力猛击软木塞时对底部施加的额外力。
    4. 某种液压系统被设计为施加的力是其施加的力量的100倍。 (a) 被控制的气缸面积与主缸面积的比例必须是多少？ (b) 它们的直径之比必须是多少？ (c) 相对于输入力移动的距离，输出力移动的距离减少了多少系数？ 假设没有摩擦造成的损失。
    5. 假设没有摩擦损失，验证液压系统的功率输入是否等于工作输出。 为此，显示输出力移动距离的减小系数与输出力增加的系数相同。 假设流体的体积是恒定的。 流体内部和系统中组件之间的摩擦会对输出力产生什么影响？ 这将如何取决于流体是否在移动？

    14.4 阿基米德原理和浮力

    1. 鉴于 0 °C 时的水密度非常接近 1000 kg/m 3，那么漂浮在淡水中时，有多少部分的冰会被淹没？
    2. 如果一个人的身体密度为995 kg/m 3，那么在（a）淡水中轻轻漂浮时，身体的多少部分会被淹没？ (b) 在密度为 10 27 kg/m 3 的盐水中？
    3. 发现空气中质量为 540 g 的岩石在浸入水中时其表观质量为 342 g。 (a) 有多少量的水被排出？ (b) 岩石的体积是多少？ (c) 它的平均密度是多少？ 这与花岗岩的价值一致吗？
    4. 阿基米德原理可用于计算流体的密度和固体的密度。 假设发现一块空气中质量为390.0 g的铁在完全浸入未知液体中时其表观质量为350.5 g。 (a) 铁会取代多少质量的液体？ (b) 根据表14.1给出的密度，铁的体积是多少？ (c) 计算流体的密度并进行识别。
    5. (a) 计算 2.00L 氦气球上的浮力。 (b) 鉴于气球中橡胶的质量为 1.50 g，如果气球松开，气球上的净垂直力是多少？ 忽略橡胶的体积。
    6. (a) 漂浮在淡水中，体积的4.00％在水面以上的女性的密度是多少？ （这可以通过将她放在侧面有标记的水箱中来衡量，以测量她在漂浮时和被困在水下时会移出多少水。） (b) 当她漂浮在海水中时，她的体积中有多少百分比在水面以上？
    7. 一个人的体重为80千克，密度为955千克/立方米（不包括肺部的空气）。 (a) 计算他的音量。 (b) 找到空中对他施加的浮力。 (c) 浮力与他的体重之比是多少？
    8. 一个简单的指南针可以通过在漂浮在水中的软木塞上放一块小条形磁铁来制成。 (a) 漂浮在水中时，普通软木塞中有多少部分会被淹没？ (b) 如果软木塞的质量为 10.0 g，并在上面放置了 20.0 克的磁铁，那么软木塞的多少部分会被淹没？ (c) 棒状磁铁和软木塞会漂浮在乙醇中吗？
    9. 当铁锚浸入盐水中时，浮力会支撑多少百分比的重量？
    10. 参照图 14.20，证明气缸上的浮力等于移位流体的重量（阿基米德原理）。 你可以假设浮力为 F 2 − F 1，圆柱体两端的面积相等 A。请注意，圆柱体（及其取代的流体）的体积等于 (h 2 − h 1) A。
    11. 一个75.0公斤的人漂浮在淡水中，当他的肺空时，其体积的3.00％在水面上，而当他的肺满时，他的体积的5.00％在水面上。 (a) 以升为单位计算他吸入的空气量（称为肺活量）。 (b) 这个肺容量看起来合理吗？

    14.5 流体动力学

    1. 如果平均流量为 10.0 km/L，则汽油流向以 100 km/h 的速度行驶的汽车发动机的平均流量是多少（以 cm 3 /s 为单位）？
    2. 静息成人的心脏以 5.00 L/min 的速度抽血。 (a) 将其转换为 cm 3 /s。(b) 以 m 3 /s 为单位的这个速率是多少？
    3. 怀卡托河上的胡卡瀑布是新西兰访问量最大的自然旅游景点之一。 平均而言，这条河的流速约为300,000升/秒。在峡谷中，河流的宽度变窄到20米，平均深度为20米。 (a) 峡谷中河流的平均速度是多少？ (b) 当瀑布下游河流扩大到60米并且其深度增加到平均40米时，水的平均速度是多少？
    4. (a) 估计使用输送60升/分钟的花园软管填满容量为80,000升的私人游泳池所需的时间。 (b) 如果你能将一条以 5000 m 3 /s 的速度流入水池的中等大小的河流需要多长时间？
    5. (a) 直径为 9.00 厘米的消防水带每秒输送 80.0 L 水的流体速度是多少？ (b) 以立方米/秒为单位的流速是多少？ (c) 如果盐水取代消防水带中的淡水，你的答案会有所不同吗？
    6. 水以 2.00 m/s 的速度通过内径为 1.60 cm 的软管流动。 (a) 以升/秒为单位的流速是多少？ (b) 该软管喷嘴中的流体速度为 15.0 m/s。喷嘴的内径是多少？
    7. 证明不可压缩流体通过收缩（例如在文丘里管中）的速度增加一个系数，等于直径减小系数的平方。 （反之则适用于从收缩区流出到更大直径区域的流动。）
    8. 水直接从直径为1.80厘米的水龙头中流出，速度为0.500 m/s。（由于水龙头的构造，水流的速度没有变化。） (a) 以 cm 3 /s 为单位的流速是多少？ (b) 水龙头下方 0.200 米的水流直径是多少？ 忽略因表面张力而产生的任何影响。

    14.6 伯努利方程

    1. 验证压力是否以单位体积的能量为单位。
    2. 假设你有一个风速计，比如图 14.32 所示的皮托管。 风速必须增加什么系数才能使压力计中 h 值的两倍？ 这与运动流体和压力计中的流体无关吗？
    3. 如果你的皮托管的压力读数为 15.0 mm Hg，速度为 200 km/h，那么在相同海拔下 700 km/h 的压力读数会是多少？
    4. 每隔几年，当早春喷气流下降时，科罗拉多州博尔德的风速就会达到45.0 m/s（约每小时 100 英里/小时）的持续速度。 在面积为 220m 2 的屋顶上，伯努利方程产生的力大约是多少？ 博尔德的典型空气密度为1.14 kg/m 3，相应的大气压力为 8.89 x 10 4 N/m 2。 （文本中所述的伯努利原理假设层流动。 这里使用原理只能产生近似的结果，因为存在明显的湍流。）
    5. (a) 伯努利效应导致的压降是多少，因为水从直径为9.00厘米的消防水带进入直径为3.00厘米的喷嘴，同时输送流量为40.0 L/s？ (b) 这个水可以上升到喷嘴上方的最大高度？ （由于空气阻力，实际高度会明显变小。）
    6. (a) 使用伯努利方程，显示皮托管测得的流体速度 v（如图 14.32 (b) 所示）由 v =\(\left(\dfrac{2 \rho' gh}{\rho} \right)^{1/2}\) 给出，其中 h 是压力计流体的高度，\(\rho′\)是压力计流体的密度，\(\rho\)是移动流体的密度，g 是重力引起的加速。 （请注意，如文中所述，v 确实与 h 的平方根成正比。） (b) 如果水银压力计的 h 为 0.200 m，则计算流动空气的 v。
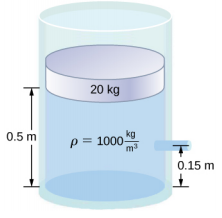
    7. 水容器的横截面积为 A = 0.1 m 2。 活塞位于水的顶部（见下图）。 有一个喷嘴位于水箱底部 0.15 米处，通向大气，水流从喷嘴流出。 喷嘴的横截面积为 A s = 7.0 x 10 −4 m 2。 (a) 水离开喷嘴时的速度是多少？ (b) 如果喷嘴的开口距离地面 1.5 米，那么水落到地板的距离有多远？ 忽略所有摩擦力和耗散力。

    该图是一个装满流体并一侧向大气开口的圆柱体的示意图。 在流体中放置一个质量为 20 kg 的圆盘，表面积 A 与圆柱体的表面积相同。 它位于容器底部上方半米处。 一个通向大气的喷嘴位于距离水箱底部 0.15 米处。

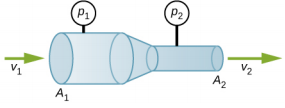
    1. 恒定密度的流体流过管道中的凹槽。 找出压力变化的方程，以 v 1、A 1、A 2 和密度表示。

    图为从横截面区域 A1 缩小到横截面区域 A2 的管线示意图。 流体流过管道。 管道不同部分的压力和流体速度不同。 它们在宽横截面中为 P1 和 v1，在窄横截面区域为 P2 和 v2。

    14.7 粘度和湍流

    1. (a) 根据以下信息，计算由推车和水平空中轨道之间的空气层粘度产生的减速力：空气温度为 20 °C，手推车以 0.400 m/s 的速度移动，其表面积为 2.50 x 10 −2 m 2，空气层的厚度为 6.00 x 10−5 m。(b) 这种力与 0.300 千克手推车重量的比例是多少？
    2. 通往器官的小动脉（小动脉）收缩以减少流向器官的流量。 为了关闭器官，血流量自然减少到其原始值的1.00％。 小动脉的半径通过什么因素收缩？
    3. 以极限速度落入液体中的球形粒子必须通过阻力和浮力来平衡重力。 浮力等于移位流体的重量，而阻力假定由斯托克斯定律给出，F s = 6\(\pi \eta\) v。显示终端速度由 v = 给出\(\frac{2R^{2} g}{9 \eta} (\rho_{s} − \rho_{1})\)，其中 R 是球体的半径，\(\rho_{s}\)是球体的密度，\(\rho_{1}\)是球体的密度流体和粘\(\eta\)度系数。
    4. 使用前面问题的方程式，求出半径为 0.8 mm 的钢球落下、终端速度为 4.32 cm/s 的机油的粘度。滚珠和机油的密度分别为 7.86 和 0.88 g/mL。
    5. 当空中阻力等于他或她的体重时，跳伞运动员将达到终极速度。 对于体型较大的跳伞运动员来说，湍流是高速运动中的一个因素。 然后，阻力与速度的平方大致成正比。 将阻力设为 F D =\(\frac{1}{2} \rho Av^{2}\)，并将其设置为等于跳伞运动员的体重，找到落下 “传播鹰” 的人的终端速度。
    6. (a) 假设所有其他因素保持不变，验证通过管道的层流减少19.0％是由于半径减少5.00％造成的。 (b) 假设所有其他因素保持不变，半径增加 5.00% 会增加多少流量？
    7. 当医生诊断出动脉阻塞时，他们会引述流速的降低。 如果血块使动脉的流速降低到其正常值的10.0％，并且平均压差增加了20.0％，那么血块使动脉半径缩小了什么因素？
    8. 喷油器通过直径为0.100米的管道向空中喷射25.0米的原油。 忽略空气阻力而不考虑管道阻力，假设层流，计算50.0米长的垂直管道入口处的压力。 假设油的密度为 900 kg/m 3，其粘度为 1.00 (N/m 2) • s（或 1.00 Pa•s）。 请注意，必须考虑由于管道中有 50.0 米的油柱而产生的压力。
    9. 混凝土从水泥搅拌机泵送到正在铺设的地方，而不是用独轮车运输。 流速为 200 升/分钟，通过一根长 50.0 米、直径为 8.00 厘米的软管，泵的压力为 8.00 x 10 6 N/m 2。 (a) 计算软管的阻力。 (b) 假设水流是层状的，混凝土的粘度是多少？ (c) 假设使用点与泵处于同一水平，正在提供多少功率？ 你可能会忽略为提高混凝土速度而提供的动力。
    10. 验证喷油器的油流是否为层流，该喷油器通过直径为 0.100 米的管道将原油喷射到空中 25.0 m。 垂直管道长 50 米。 假设油的密度为 900 kg/m 3，其粘度为 1.00 (N/m 2) • s（或 1.00 Pa•s）。
    11. 计算当喷嘴连接到软管上时（a）半径为 0.250 cm 的喷嘴和（b）半径为 0.900 cm 的花园软管的水流的雷诺数。 通过软管和喷嘴的流速为 0.500 L/s。两者中的流量可能是层流吗？
    12. 消防水带的内径为 6.40 厘米。 假设这样的软管在表压为 1.62 x 10 6 N/m 2 时输送的流量为 40.0 L/s。 软管沿梯子向上延伸 10.0 m，到达内径为 3.00 cm 的喷嘴。 计算消防水带和喷嘴中流量的雷诺数，以表明每个水带和喷嘴中的流量必须是湍流的。
    13. 直径为 0.200 米的供水管道以什么流速开始出现湍流？ 假设温度为 20 °C。

    其他问题

    1. 在数字存储设备（例如手机中的内存）出现之前，音乐存储在黑胶唱片上，磁盘上有不同深度的凹槽。 留声机使用了在凹槽上移动的针头来测量凹槽的深度。 留声机针头在唱片上施加的压力出人意料地大。 如果一根针头支撑相当于 1.00 g 的重量，其尖端是一个半径为 0.200 mm 的圆圈，那么以 Pa 为单位对记录施加的压力是多少？
    2. 在大量使用时，水塔储存的水量超过消费者的水平，从而无需使用高速水泵。 要产生 3.00 x 10 5 N/m 2 的表压，水位必须高于用户？
    3. 人眼中的房水对角膜 1.10 cm 2 区域施加 0.300 N 的力。 这个压力是多少，单位是毫米汞柱？
    4. (a) 使用液体重量引起的压力关系（p = h g）而不是换算系数，将超过 80 mm H\(\rho\) g 的 120 个正常血压读数转换为每米牛顿的平方。 (b) 解释为什么婴儿的血压可能低于成人的血压。 具体而言，请考虑必须将血液输送到较小的高度。
    5. 压力锅已经存在了300多年，尽管近年来它们的使用量已大大下降（早期型号有一种讨厌的爆炸习惯）。 如果圆形盖子的直径为 25.0 厘米，里面的表压为 300 atm，那么将盖子固定在压力锅上的闩锁必须能够承受多大的力？ 忽略盖子的重量。
    6. 鸟骨里面有气穴以减轻体重，这也使它们的平均密度明显低于其他动物的骨头。 假设鸟类学家在空气和水中称重一根鸟骨，发现其质量为45.0 g，水下时的表观质量为3.60 g（假设骨头是防水的）。 (a) 有多少量的水被排出？ (b) 骨头的体积是多少？ (c) 它的平均密度是多少？
    7. 在对女性密度的浸泡测量中，发现她在空气中的质量为62.0 kg，在肺部空着的情况下完全浸入水中的表观质量为0.0850 kg。 (a) 她取代了多少质量的水？ (b) 她的音量是多少？ (c) 计算她的密度。 (d) 如果她的肺活量为1.75 L，她能否在肺部充满空气的情况下不用踩水就能漂浮？
    8. 有些鱼的密度略低于水的密度，必须施加力量（游泳）才能保持水下状态。 如果体密度为 1015 kg/m 3，85.0 千克的石斑鱼必须施加什么力量才能浸入盐水中？
    9. 人体循环系统有大约 1 x 10 9 个毛细血管。 每条血管的直径约为 8\(\mu\) m。假设心输出量为 5 L/min，则确定流经每根毛细血管的平均血流速度。
    10. 通过 2.00 x 10 −6 m 半径毛细血管的血液流速为 3.80 x 10 9 cm 3 /s。(a) 血液流动的速度是多少？ (b) 假设体内的所有血液都通过毛细血管，那么必须有多少毛细血管才能输送总流量为90.0 cm 3 /s？
    11. 静息成年人心脏的左心室以 83.0 cm 3 /s 的流速抽血，压力增加 110 mm Hg，速度从零增加到 30.0 cm/s，高度增加 5.00 cm。 （所有数字均为整个心跳的平均值。） 计算左心室的总功率输出。 请注意，大部分力量用于增加血压。
    12. 污水泵（用于从地下水位以下建造的房屋的地下室排水）正在以0.750 L/s的速度排干被洪水淹没的地下室，输出压力为3.00 x 10 5 N/m 2。 (a) 水进入内径为3.00厘米的软管，上升至泵上方2.50米。 此时它的压力是什么？ (b) 软管越过基础墙，高度下降0.500米，直径扩大到4.00厘米。 现在的压力是多少？ 你可能会忽略问题两个部分的摩擦损失。
    13. 静脉注射给药的葡萄糖溶液的流速为 4.00 cm 3 /min 如果葡萄糖被密度相同但粘度为葡萄糖2.50倍的全血所取代，新的流速会是多少？ 所有其他因素保持不变。
    14. 一条小动脉的长度为 1.1 x 10 −3 m，半径为 2.5 x 10 −5 m。如果穿过动脉的压降为 1.3 kPa，则通过动脉的流速是多少？ （假设温度为 37 °C。）
    15. 血管成形术是一种扩张部分被斑块阻塞的动脉以增加血液流动的技术。 为了将血流量增加10倍，动脉的半径必须增加哪个系数？
    16. 假设血管的半径因斑块沉积而减小到其原始值的90.0％，身体通过增加血管沿线的压力差来进行补偿，以保持流速恒定。 (a) 压差必须增加什么系数？ (b) 如果湍流是由障碍物造成的，它会对流速产生什么额外影响？

    挑战问题

    1. 问题部分前面显示的大坝压力随着深度的增加而增加。 因此，大坝上存在净扭矩。 找到净扭矩。
    2. 大气的温度并不总是恒定的，并且会随着高度而升高或降低。 在中性气氛中，没有大量的垂直混合，温度以每千米大约 6.5 K 的速度降低。 随着身高的增加，温度下降的幅度被称为失效率 (γ)。 （符号是大写的希腊字母 gamma。） 假设表面压力为 p 0 = 1.013 x 10 5 Pa，其中 T = 293 K，失效率为（\(\Gamma\)= 6.5 K/km）。 估计地球表面 3.0 km 以上的压力。
    3. 一艘潜艇滞留在海底，其舱口位于海面以下 25.0 米处。 假设舱口是圆形的，直径为 0.450 m，计算从内部打开舱口所需的力。 潜艇内的气压为 1.00 atm。
    4. 原木有时会垂直漂浮在湖中，因为一端被淹水了，比另一端更密集。 漂浮在水面上方长度为20.0％的均匀直径原木的平均密度是多少？
    5. 众所周知，邪恶的骗子们将镀金钨锭描述为纯金，并以远低于黄金价值但高于钨价格的价格出售。 你必须能够以多大的精度测量这种进出水的锭的质量，才能分辨出它几乎是纯钨而不是纯金？
    6. 房屋的内部体积相当于宽13.0米、长20.0米、高2.75米的矩形实体的体积。 房子由强制空气燃气加热器加热。 加热器的主吸气管道直径为 0.300 m。 如果管道每隔15分钟输送的空气量等于房屋内部的空气量，则该管道中的平均空气速度是多少？
    7. 直径为2.0厘米的花园软管用于填充容积为0.10立方米的水桶。 填满需要 1.2 分钟。 软管上安装了一个可调节的喷嘴，以减小开口的直径，从而提高水的速度。 软管在 1.0 米的高度与地面保持水平，直径会减小，直到到达 3.0 米外的花坛。 (a) 当直径为 2.0 cm 时，水通过喷嘴的体积流速是多少？ (b) 水从软管流出的速度是多少？ (c) 水从软管流出的速度需要多少才能到达 3.0 米外的花坛？ (d) 到达花坛所需的喷嘴直径是多少？
    8. 飞机设计中经常引用的经验法则是，机翼每平方米的机翼应产生大约 1000 N 的升力。 （机翼有顶部和底部表面这一事实并不能使其面积增加一倍。） (a) 起飞时，飞机以60.0 m/s的速度行驶，因此相对于机翼底部的空速为60.0 m/s。鉴于空气的海平面密度为1.29 kg/m 3，它必须以多快的速度在上表面移动才能产生理想的升力？ (b) 空气以 245 m/s 的巡航速度在空气密度为海平面四分之一的高度上空移动的速度必须有多快？ （请注意，这还不是飞机的全部升力，有些来自飞机机身，有些来自发动机推力，依此类推。 此外，伯努利原理给出了近似的答案，因为流过机翼会产生湍流。）
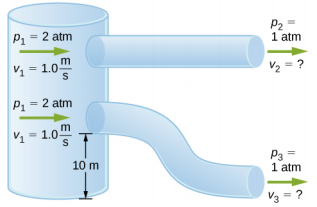
    9. 两条直径相等且恒定的管道离开抽水站，将水从向大气开放的开口端排出（见下图）。 水在两个大气压的压力下进入，速度为（v 1 = 1.0 m/s）。 一根管道落下 10 米的高度。水离开每根管道时水的速度是多少？

    图为两条直径相等且恒定的管道的示意图。 它们一侧向大气开放，另一侧与装满水的水箱相连。 底部管道的连接距离地面 10 米。

    1. 流体最初以 100 cm 3 /s 的速率流过管道。为了说明流速对各种因素的敏感性，计算以下变化的新流速，所有其他因子都与原始条件保持不变。 (a) 压力差增加1.50倍。 (b) 使用粘度高出3.00倍的新流体代替。 (c) 用长度为4.00倍的管子代替。 (d) 使用另一根半径为原始管道的0.100倍。 (e) 另一根管子被替换，其半径为原来的0.100倍，长度为一半，压差增加了1.50倍。
    2. 在马拉松比赛中，跑步者的血流量增加到其静息速度的10.0倍。 她的血液粘度已降至正常值的95.0％，整个循环系统的血压差增加了50.0％。 她的血管平均半径通过什么因素增加？
    3. 在夏日早些时候，社区用水量较低时，自来水管道向房屋供水的压力为3.00 x 10 5 N/m 2。 该压力通过花园软管产生 20.0 L/min 的流量。 当天晚些时候，水管出口和房屋入口处的压力下降，通过同一根软管获得的流量仅为8.00 L/min。 (a) 假设阻力恒定，现在向房屋提供的压力是多少？ (b) 为了导致输送压力的降低，供水管道的流速增加了什么因素？ 水管入口处的压力为 5.00 x 10 5 N/m 2，原始流速为 200 升/分钟。 (c) 假设每个用户在早上消耗 20.0 升/分钟，还有多少用户？
    4. 汽油通过地下管道从炼油厂输送到主要用户。 流速为 3.00 x 10 −2 m 3 /s（大约 500 加仑/分钟），汽油的粘度为 1.00 x 10 −3（N/m 2）• s，其密度为 680 kg/m 3。 (a) 如果雷诺数小于 2000，管道的最小直径必须是多少？ (b) 要保持这种流速，必须沿管道每千米保持多大的压差？

    贡献者和归因

    Template:ContribOpenStaxUni