14.9: 粘度和湍流
- Page ID
- 205056
- 解释什么是粘度
- 使用 Poiseuille 定律计算流量和阻力
- 解释压力如何因阻力而下降
- 计算在流体中移动的物体的雷诺数
- 使用系统的雷诺数来确定它是层流的还是湍流的
- 描述物体达到终端速度的条件
在引入摩擦概念的《牛顿定律的应用》中,我们看到一个物体以初始速度滑过地面,没有施加的力会由于摩擦力而静止。 摩擦力取决于接触材料的类型,与法向力成正比。 在同一章中,我们还讨论了阻力和空气阻力。 我们解释说,在低速时,阻力与速度成正比,而在高速行驶时,阻力与速度的平方成正比。 在本节中,我们将介绍作用于运动流体的摩擦力。 例如,流经管道的流体在流体和壁之间会受到阻力,这是一种摩擦。 不同流体层之间也会发生摩擦。 这些阻力影响流体流经管道的方式。
粘度和层流
当你给自己倒一杯果汁时,液体会自由快速地流动。 但是,如果你把枫糖浆倒在煎饼上,液体会缓慢流动并粘在水壶里。 区别在于流体内部以及流体与其周围环境之间的流体摩擦力。 我们称这种流体的特性为粘度。 果汁的粘度低,而糖浆的粘度很高。
粘度的精确定义基于层流或非湍流。 \(\PageIndex{1}\)该图示意性地显示了层流和湍流的区别。 当层流为层流时,层流不混合。 当流动是湍流时,各层混合在一起,并且在总体流动方向以外的方向上出现明显的速度。
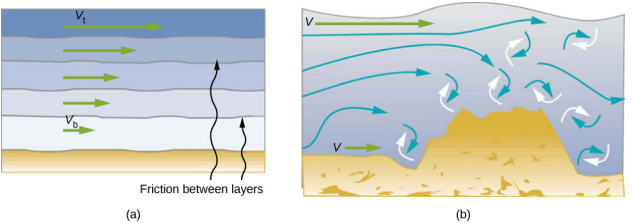
湍流是一种流体流,其中各层通过涡流和漩涡混合在一起。 它有两个主要原因。 首先,任何障碍物或尖角,例如水龙头中的障碍物或尖角,都会通过赋予垂直于水流的速度来产生湍流。 其次,高速会导致湍流。 如果速度足够快,相邻流体层之间以及流体与其周围环境之间的阻力可能会形成漩涡和涡流。 在图中\(\PageIndex{2}\),由于烟雾和周围空气之间的阻力,加速烟雾的速度达到了开始旋转的程度。

\(\PageIndex{3}\)该图显示了如何测量流体的粘度。 要测量的流体放置在两个平行板之间。 底板保持固定,而顶板向右移动,随之拖动流体。 与任一板接触的流体层(或薄层)不会相对于板移动,因此顶层以 v 的速度移动,而底层保持静止状态。 自上而下的每个连续层对其下方的层施加力,试图将其向前拖动,从而产生从 v 到 0 的速度连续变化,如图所示。 注意确保流量是层状的,也就是说,各层不会混合。 图中的动作就像连续的剪切动作。 流体的剪切强度为零,但它们的剪切速率与固体剪切变形相同的几何因子 A 和 L 有关。 在图中,流体最初处于静止状态。 由于移动板和流体之间的内部摩擦,与移动板接触的流体层加速并开始移动。 下一层与移动层接触;由于两层之间存在内部摩擦,它也会加速,依此类推,穿过流体的深度。 固定板和站板旁边的最低流体层之间也存在内部摩擦。 由于内部摩擦,需要用力来保持板以恒定速度移动。
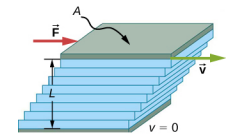
需要力 F 才能使图中的顶板以恒定速度 v\(\PageIndex{3}\) 移动,实验表明,该力取决于四个因素。 首先,F 与 v 成正比(直到速度如此之高以至于发生湍流,然后需要更大的力,而且它对 v 的依赖性更为复杂)。 其次,F 与板的面积 A 成正比。 这种关系似乎是合理的,因为 A 与移动的流体量成正比。 第三,F 与板块之间的距离成反比。这种关系也是合理的;L 就像杠杆臂,杠杆臂越大,所需的力就越少。 第四,F 与粘度系数成正比,\(\eta\)粘度越大,所需的力越大。 这些依赖关系合并到方程中
\[F = \eta \frac{vA}{L} \ldotp\]
这个方程为我们提供了流体粘度的有效定义\(\eta\)。 求\(\eta\)解
\[\eta = \frac{FL}{vA} \label{14.17}\]
它根据如何测量粘度来定义粘度。 粘度的 SI 单位为\(\frac{N\; \cdotp m}{[(m/s)m^{2}]}\) = (N/m 2) s 或 Pa • s。表\(\PageIndex{1}\)列出了各种流体的粘度系数。 粘度从一种流体到另一种流体有几个数量级的差异。 正如你所预料的那样,气体的粘度远低于液体的粘度,这些粘度通常取决于温度。
| 流体 | 温度 (°C) | 粘度\(\eta \times 10^{3}\) |
|---|---|---|
| 空气 | 0 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >0.0171 |
| 20 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >0.0181 | |
| 40 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >0.0190 | |
| 100 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >0.0218 | |
| 氨水 | 20 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >0.00974 |
| 二氧化碳 | 20 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >0.0147 |
| 氦气 | 20 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >0.0196 |
| 氢气 | 0 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >0.0090 |
| 水星 | 20 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >0.0450 |
| 氧气 | 20 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >0.0203 |
| 蒸汽 | 100 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >0.0130 |
| 液态水 | 0 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >1.792 |
| 20 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >1.002 | |
| 37 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >0.6947 | |
| 40 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >0.653 | |
| 100 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >0.282 | |
| 全血 | 20 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >3.015 |
| 37 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >2.084 | |
| 血浆 | 20 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >1.810 |
| 37 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >1.257 | |
| 乙醇 | 20 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >1.20 |
| 甲醇 | 20 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >0.584 |
| 油(重型机器) | 20 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >660 |
| 机油(发动机,SAE 10) | 30 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >200 |
| 油(橄榄) | 20 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >138 |
| 甘油 | 20 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >1500 |
| 亲爱的 | 20 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >2000-10000 |
| 枫糖浆 | 20 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >2000-3000 |
| 牛奶 | 20 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >3.0 |
| 油(玉米) | 20 | \ (\ eta\ times 10^ {3}\)” style= “text-align: center;” class= “lt-phys-4714” >65 |
层流局限于管道:泊西耶定律
什么原因导致流动? 毫不奇怪,答案是压力差。 实际上,水平流量和压力之间存在着非常简单的关系。 流速\(Q\)是从高压到低压的方向。 两点之间的压差越大,流速越大。 这种关系可以说是
\[Q = \frac{p_{2} - p_{1}}{R}\]
其中\(p_1\)和\(p_2\)是两点的压力,例如管道两端的压力,\(R\)是流动阻力。 阻力\(R\)包括影响流速的所有因素,压力除外。 例如\(R\),长管比短管更大。 流体的粘度越大,其值越大\(R\)。 湍流会大大增加 R,而增加管道直径会减小\(R\)。
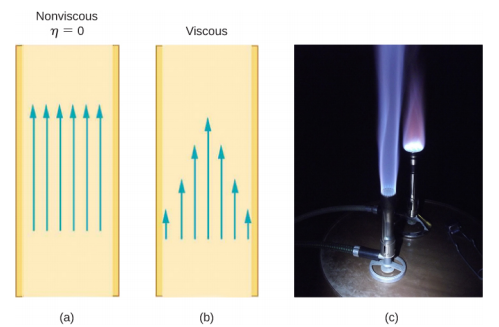
如果粘度为零,则流体无摩擦,流动阻力也为零。 将管道中的无摩擦流与粘性流进行比较,如图所示\(\PageIndex{4}\),我们可以看出,对于粘性流体,由于边界阻力,中游速度最快。 尽管天然气的粘度很小,但我们可以看到粘度对本生燃烧器火焰的影响 [第 (c) 部分]。
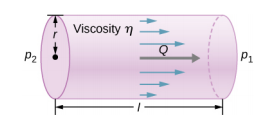
粘度\(\eta\)为均匀半径 r 和长度 l 的水平管的不可压缩流体对层流的阻力 R 由下式给出
\[R = \frac{8 \eta l}{\pi r^{4}} \ldotp \label{14.18}\]
这个方程被称为泊西耶抵抗定律,以法国科学家 J.L. Poiseuille(1799—1869 年)的名字命名,他得出这个方程的目的是为了了解血液在人体中的流动。
让我们来看看 Poiseuille 对 R 的表达式,看看它是否具有良好的直观意义。 我们可以看到,阻力与流体粘\(\eta\)度和管道长度 l 成正比。 毕竟,这两者都直接影响所遇到的摩擦量——两者都越大,阻力越大,流量越小。 管的半径 r 会影响阻力,这也是有道理的,因为半径越大,流量越大(所有其他因素保持不变)。 但令人惊讶的是,r 被提升到泊西耶定律中的第四次权力。 这个指数意味着管道半径的任何变化都会对阻力产生非常大的影响。 例如,将管的半径加倍会使阻力降低系数 2 4 = 16。
总\(Q = \frac{p_{2} - p_{1}}{R}\)而言之,\(R = \frac{8 \eta l}{\pi r^{4}}\)给出以下流速表达式:
\[Q = \frac{(p_{2} - p_{1}) \pi r^{4}}{8 \eta l} \ldotp \label{14.19}\]
该方程描述了穿过管道的层流。 它有时被称为层流的泊西耶定律,或者简称为 Po iseuille 定律(图\(\PageIndex{5}\))。
正在设计一种空调系统,用于在20°C的温度下以0.054 Pa的表压供应空气。空气通过直径为18.00 cm的绝缘圆形管道输送。 管道长 20 米,通向大气压为 101.30 kPa 的房间。 房间长 12 米,宽 6 米,高 3 米。 (a) 假设层流,通过管道的体积流速是多少? (b) 估计完全更换房间内空气所需的时间长度。 (c) 建筑商决定使用直径为9.00厘米的管道来省钱。 新的流量是多少?
策略
假设层流,泊西耶定律指出
\[Q = \frac{(p_{2} - p_{1}) \pi r^{4}}{8 \eta l} = \frac{dV}{dt} \ldotp \nonumber\]
我们需要比较流量降低前后的动脉半径。 请注意,我们得到的是导管的直径,因此我们必须除以二才能得到半径。
解决方案
- 假设压差恒定并使用粘度\(\eta = 0.0181\; mPa\; \cdotp s\),$$Q =\ frac {(0.054\; Pa) (3.14) (0.09\; m) ^ {4}} {8 (0.0181\ times 10^ {-3}\; Pa\;\ cdotp s) (20\; m)} = 3.84\ times 10^ {-3}\; m^ {3} /s\ ldotp$$
- 假设流量恒定\(Q = \frac{dV}{dt} \approx \frac{\Delta V}{\Delta t}\) $$\ Delta t =\ frac {\ Delta V} {Q} =\ frac {(12\; m) (6\; m) (3\; m)} {3.84\ times 10^ {-3}\; s = 5.63\ times 10^ {4}\; s = 15.63\; hr\ ldotp\ nonumber$$
- 使用层流,泊西耶定律得出 $Q =\ frac {(0.054\; Pa) (3.14) (0.045\; m) {4}} {8 (0.0181\ times 10^ {-3}\; Pa\;\ cdotp s) (20\; m)} = 22.40\ times 10^ {-4}\; m^ {3} /s\ ldotp$s $因此,管道的半径减小一半会将流速降低到原始值的6.25%。
意义
通常,假设层流,减小半径比改变长度具有更显著的效果。 如果长度增加并且所有其他变量保持不变,则流速会降低:
\[\begin{split} \frac{Q_{A}}{Q_{B}} & = \frac{\frac{(p_{2} - p_{1}) \pi r_{A}^{4}}{8 \eta l_{A}}}{\frac{(p_{2} - p_{1}) \pi r_{B}^{4}}{8 \eta l_{B}}} = \frac{l_{B}}{l_{A}} \\ Q_{B} & = \frac{l_{A}}{l_{B}} Q_{A} \ldotp \end{split} \nonumber\]
将长度加倍会将流速减至原始流速的一半。
如果半径减小且所有其他变量保持不变,则体积流速会降低一个更大的系数。
\[\begin{split} \frac{Q_{A}}{Q_{B}} & = \frac{\frac{(p_{2} - p_{1}) \pi r_{A}^{4}}{8 \eta l_{A}}}{\frac{(p_{2} - p_{1}) \pi r_{B}^{4}}{8 \eta l_{B}}} = \left(\dfrac{r_{A}}{r_{B}}\right)^{4} \\ Q_{B} & = \left(\dfrac{r_{B}}{r_{A}}\right)^{4} Q_{A} \end{split}\]
将半径切成两半会将流速降低到原始流速的十六分之一。
流量和阻力是压力下降的原因
在大量使用期间,例如炎热的夏季,家庭水压有时会低于正常水平。 压力下降发生在供水管道到达个人住宅之前。 让我们考虑一下流经水管道的流量,如图所示\(\PageIndex{6}\)。 通过重新排列流量方程式,我们可以理解为什么在大量使用时家中的压力 p 1 会下降:
\[\begin{align} Q & = \frac{p_{2} - p_{1}}{R} \\[4pt] p_{2} - p_{1} & = RQ . \label{EQ5} \end{align}\]
在这种情况下,\(p_2\)是自来水厂的压力,\(R\)是供水管道的阻力。 在大量使用期间,流速\(Q\)很大。 这意味着它也\(p_2 − p_1\)必须很大。 因此\(p_1\)必须减少。 将流量和阻力视为导致压力从 p 2 下降到 p 1 是正确的。 方程 p 2 − p 1 = RQ 对层流和湍流都有效。

我们还可以使用方程\ ref {EQ5} 来分析在更复杂的系统中发生的压降,在这些系统中,管道半径在所有地方都不相同。 在狭窄的地方,例如冠状动脉阻塞,阻力要大得多。 对于给定的流量 Q,管道最窄处的压降最大。 水龙头就是这样控制水流的。 此外,湍流会大大增加 R,而产生湍流的收缩会大大降低下游的压力。 动脉中的斑块通过其阻力和产生的湍流来降低压力,从而降低流动。
测量湍流
称为雷诺数的指示器\(N_R\)可以显示流量是层流还是湍流。 对于直径均匀的管道中的流动,雷诺数定义为
\[N_{R} = \frac{2 \rho vr}{\eta}\; (flow\; in\; tube) \label{14.20}\]
其中\(\rho\)是流体密度,v 其速度、\(\eta\)粘度和管\(r\)道半径。 雷诺数是一个无量纲量。 实验表明,\(N_R\)这与湍流的开始有关。 对于 N R 低于 2000 左右,流量为层流。 对于大\(N_R\)约 3000,流量是湍流的。
对于介于 2000 和 3000\(N_R\) 之间的值,流量是不稳定的,也就是说,它可以是层状的,但是小的障碍物和表面粗糙度会使其湍流,并且可能在层流和湍流之间随机振荡。 实际上,雷诺数介于 2000 和 3000 之间的流体的流动就是混乱行为的一个很好的例子。 当一个系统的行为对某些因素非常敏感以至于很难预测时,它就被定义为混乱。 当流体的雷诺数落在此范围内时,很难预测流体是否为湍流,但并非不可能,这是因为对粗糙度和阻塞物等因素对流动性质的依赖性极为敏感。 一个因子的微小变化会对流量产生夸大(或非线性)影响。
在示例 14.8 中,我们发现空调系统的体积流速为 Q = 3.84 x 10 −3 m 3 /s。此计算假设为层流量。
- 这是个好假设吗?
- 水流会以什么速度变成湍流?
策略
要确定通过空调系统的空气流是否为层流,我们首先需要找到速度,可以通过以下方式找到
\[Q = Av = \pi r^{2} v \ldotp \nonumber\]
然后我们可以使用以下方程计算雷诺数,并确定它是否落在层流范围内
\[R = \frac{2 \rho vr}{\eta} \ldotp \nonumber \]
解决方案
- 使用给定的值:$$\ begin {split} v & =\ frac {Q} {\ pi r^ {2}} =\ frac {3.84\ times 10^ {-3}\; m^ {3} /s} {3.14 (0.09\; m) ^ {2\\ R & =\ frac {2\ rho vr} {\ eta} = frac {2 (1.23\; kg/m^ {3}) (0.15\; m/s) (0.09\; m)} {0.0181\ times 10^ {-3}\; Pa\;\ cdotp s} = 1835\ ldotp\ end {split} $自雷诺兹以来数字是 1835 < 2000,流量是层流的,不是湍流的。 假设流量是层流是正确的。
- 要找到保持层流的最大空气速度,请考虑雷诺数。 $$\ begin {split} R & =\ frac {2\ rho vr} {\ eta}\ leq 2000\\ v & =\ frac {2000 (0.0181\ times 10^ {-3}\; Pa\;\ cdotp s)} {2 (1.23\; kg/m^ {3}) (0.09\; m)} = 0.16\;\ ldotp\ end split} $$
意义
将流体从一个点转移到另一个点时,需要限制湍流。 湍流会浪费能量,因为一些用于移动流体的能量在涡流形成时会消失。 在这种情况下,一旦速度超过0.16 m/s,空调系统的效率就会降低,因为这是湍流开始发生的时刻。


