14.8: 伯努利方程

Last updated
Save as PDF

Page ID: 205076

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

解释伯努利方程中的术语
解释伯努利方程与能量守恒有何关系
描述如何从伯努利方程中推导出伯努利原理
使用伯努利原理进行计算
描述伯努利原理的一些应用

如图 14.7.4 所示，当流体流入较窄的通道时，其速度会增加。这意味着它的动能也增加了。增加的动能来自于为将流体推入通道而对流体进行的网络工作。此外，如果流体改变垂直位置，则通过引力在流体上起作用。

当通道变窄时会出现压力差。这种压差会对流体产生净力，因为压力乘以面积等于力，而这种净力确实起作用。回想一下工作能量定理，

\[W_{net} = \frac{1}{2} mv^{2} - \frac{1}{2} mv_{0}^{2} \ldotp\]

完成的网络工作会增加流体的动能。因此，无论流体是否局限在管道内，快速移动的流体中的压力都会下降。

快速移动的流体中压力下降的常见例子很多。例如，浴帘有一种令人讨厌的习惯，在淋浴开启时会凸起到淋浴间。原因是高速的水流和空气流在淋浴间内产生了较低的压力区域，而另一侧的压力保持在标准大气压下。这种压差会产生净力，将窗帘向内推动。同样，当一辆汽车在高速公路上经过一辆卡车时，两辆车似乎相互拉动。原因是一样的：汽车和卡车之间的高速空气在车辆之间形成了一个较低的压力区域，而外部压力更大，它们被推到一起（图\(\PageIndex{1}\)）。早在1800年代中期，人们就观察到了这种影响，当时人们发现相反方向行驶的列车不稳定地相互倾斜。

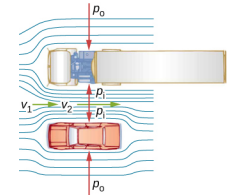
该图是一辆汽车在高速公路上经过卡车的俯视图。车辆之间的空气在较窄的通道中流动，并将速度从 v1 提高到 v2，导致车辆之间的压力从 Po 降至 Pi。 — 图\(\PageIndex{1}\)：一辆汽车在高速公路上经过卡车的俯视图。车辆之间的空气在较窄的通道中流动，必须提高其速度（v2 大于 v1），从而导致它们之间的压力下降（pi 小于 po）。外部施加的压力越大，将汽车和卡车推到一起。

节能和伯努利方程

将能量守恒原理应用于无摩擦层流可以使流体中的压力和流速之间形成非常有用的关系。这种关系被称为伯努利方程，以丹尼尔·伯努利（1700—1782 年）的名字命名，他在他的《水动力学》（1738 年）一书中发表了关于流体运动的研究。

假设流过管道的不可压缩流体具有不同的直径和高度，如图所示\(\PageIndex{2}\)。图中的下标 1 和 2 表示管道沿线的两个位置，并说明了横截面 A 的面积、流速 v、距地面高度 y 和每个点的压力 p 之间的关系。我们在这里假设两点的密度是相同的（因此，密度用\(\rho\)没有任何下标表示），而且由于不可压缩的流体，阴影体积必须相等。

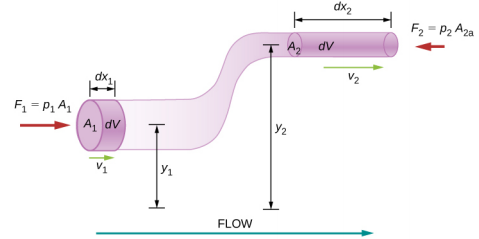
图为流体在 “S” 形管道中流动的示意图，其横截面积从 A1（左下部分）缩小到 A2（右上部分）。左下部分位于离地面 y1 的高度；右上部分位于离地面 h2 的高度。流体移动，底部为 v1，顶部为 v2。流体 dv 的体积在管道的一部分占用 dx1，在管道的顶部占用 dx2。 — 图\(\PageIndex{2}\)：用于推导伯努利方程的几何。

我们还假设流体中没有粘性力，因此流体任何部分的能量都将得到保守。为了推导伯努利方程，我们首先计算在流体上所做的工作：

\[\begin{split} dW & = F_{1} dx_{1} - F_{2} dx_{2} \\ & = p_{1} A_{1} dx_{1} - p_{2} A_{2} dx_{2} \\ & = p_{1} dV - p_{2} dV = (p_{1} - p_{2}) dV \ldotp \end{split}\]

完成的工作是由于重力的保守和流体动能的变化造成的。流体动能的变化等于

\[dK = \frac{1}{2} m_{2} v_{2}^{2} - \frac{1}{2} m_{1} v_{1}^{2} = \frac{1}{2} \rho dV (v_{2}^{2} - v_{1}^{2}) \ldotp\]

势能的变化是

\[dU = mgy_{2} - mgy_{1} = \rho dV g(y_{2} - y_{1}) \ldotp\]

然后能量方程变成

\[\begin{split} dW & = dK + dU \\ (p_{1} - p_{2}) dV & = \frac{1}{2} \rho dV (v_{2}^{2} - v_{1}^{2}) + \rho dV g(y_{2} - y_{1}) \\ (p_{1} - p_{2}) & = \frac{1}{2} \rho (v_{2}^{2} - v_{1}^{2}) + \rho g(y_{2} - y_{1}) \ldotp \end{split}\]

重新排列方程得出伯努利方程：

\[p_{1} + \frac{1}{2} \rho v_{1}^{2} + \rho gy_{1} = p_{2} + \frac{1}{2} \rho v_{2}^{2} + \rho gy_{2} \ldotp\]

这种关系表明，由于沿途压力的变化，流体任何部分的机械能都是由于该部分外部的流体所做的工作而发生的。由于这两个点是任意选择的，我们可以将伯努利方程更笼统地写成沿流的守恒原理。

伯努利方程

对于不可压缩、无摩擦的流体，压力与动能和势能密度之和的组合不仅会随着时间的推移而保持恒定，而且沿流线也是恒定的：

\[p + \frac{1}{2} \rho v^{2} + \rho gy = constant \label{14.16}\]

这里必须特别注意这样一个事实，即在动态情况下，如果流体不同部分的流速不同，则相同高度的压力可能会有所不同。

分析伯努利方程

根据伯努利方程，如果我们沿着少量流体的路径行驶，总和中的各种量可能会发生变化，但总量保持不变。实际上，伯努利方程只是一个方便的陈述，说明了在没有摩擦的情况下不可压缩流体的能量守恒。

伯努利方程的一般形式有三个项，它广泛适用。为了更好地理解它，让我们考虑一些简化和说明其用法和含义的具体情况。

静态流体的伯努利方程

首先考虑一下流体是静态的非常简单的情况，也就是说\(v_1 = v_2 = 0\)。在这种情况下，伯努利的方程为

\[p_{1} + \rho gh_{1} = p_{2} + \rho gh_{2} \ldotp\]

我们可以通过设置 h ₂ = 0 来进一步简化方程。（可以为零的参考高度选择任何高度，就像在涉及重力的其他情况下所做的那样，这使得所有其他高度都是相对的。）在这种情况下，我们得到

\[p_{2} = p_{1} + \rho gh_{1} \ldotp\]

这个方程告诉我们，在静态流体中，压力会随着深度的增加而增加。当我们在流体中从点 1 移动到点 2 时，深度增加 h ₁，因此 p ₂ 比 p ₁ 大一定量\(\rho gh_1\)。在最简单的例子中，p ₁ 在流体顶部为零，我们得到了熟悉的关系\(p = \rho gh\)。（回想一下 p =\(\rho gh\) 和\(\Delta Ug = −mgh\)。）因此，伯努利方程证实了这样一个事实，即由于流体的重量而引起的压力变化是\(\rho gh\)。尽管我们引入了伯努利流体运动方程，但它包含了我们之前研究的静态流体的大部分内容。

伯努利原理

假设流体在移动，但其深度是恒定的，即\(h_1 = h_2\)。在这种情况下，伯努利方程变为

\[p_{1} + \frac{1}{2} \rho v_{1}^{2} = p_{2} + \frac{1}{2} \rho v_{2}^{2} \ldotp \label{Bernoulli}\]

流体以恒定深度流动的情况非常常见，因此该方程通常也被称为伯努利原理，这只是伯努利恒定深度流体的方程。（再次注意，这适用于我们沿着其路径行驶的少量流体。）伯努利原理强化了这样一个事实，即运动流体中压力会随着速度的增加而下降：如果 v ₂ 大于 v ₁，则 p ₂ 必须小于 p ₁ 才能保持相等。

示例 14.6：计算压力

在示例 14.5 中，我们发现软管中的水从软管到喷嘴的速度从 1.96 m/s 提高到 25.5 m/s。计算软管中的压力，假设喷嘴中的绝对压力为 1.01 x 10 ⁵ N/m ²（必须是大气压），并且假设流量为水平无摩擦。

策略

液位流量意味着恒定的深度，因此伯努利原理适用。我们使用下标 1 表示软管中的值，使用下标 2 表示喷嘴中的值。因此，我们被要求找到 p ₁。

解决方案

求解伯努利原理（伯努利方程）以获得\(p_1\)产量

\[ \begin{align*} p_{1} &= p_{2} \frac{1}{2} \rho v_{2}^{2} - \frac{1}{2} \rho v_{1}^{2} \\[4pt] &= p_{2} + \frac{1}{2} \rho (v_{2}^{2} - v_{1}^{2}) \ldotp \end{align*}\]

替换已知值，

\[\begin{align*} p_{1} & = (1.01 \times 10^{5}\; N/m^{2}) + \frac{1}{2} (10^{3}\; kg/m^{3})[(25.5\; m/s)^{2} - (1.96\; m/s)^{2}] \\[4pt] & = 4.24 \times 10^{5}\; N/m^{2} \ldotp \end{align*}\]

意义

正如预期的那样，软管中的绝对压力大于喷嘴中的绝对压力，因为喷嘴中的v更大。喷嘴中的压力 p ₂ 必须是大气压力，因为水在没有其他条件变化的情况下进入大气层。

伯努利原理的应用

许多设备和情况都是流体以恒定高度流动，因此可以用伯努利原理进行分析。

夹带

长期以来，人们一直将伯努利原理付诸实践，在高速流体中使用减压来移动物体。当外部压力较高时，高速流体会迫使其他流体进入水流。这个过程被称为夹带。自古以来，夹带设备就被用作将水提升到较小高度的水泵，也是排干沼泽、田野或其他低洼地区所必需的。其他一些使用夹带概念的设备如图所示\(\PageIndex{3}\)。

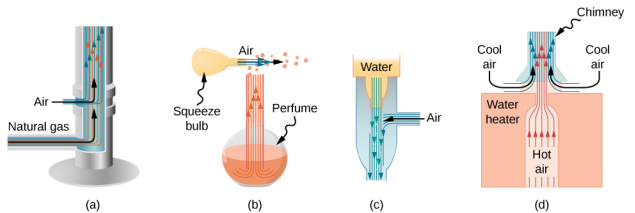
图 A 是本生燃烧器的图：空气和天然气从底部进入并向上移动。图 B 是一幅雾化器的图：挤压灯泡会产生水平流动的空气射流，将移动的香水滴向上拉出瓶子。图 C 是一幅普通吸气器的图，该吸气器的水从上到下移动，并与从侧面进入的空气流相结合。图 D 是一幅烟囱图，其中热空气向上移动，冷空气从侧面进入。 — 图\(\PageIndex{3}\)：夹带设备使用更高的流体速度来产生低压力，然后将一种流体夹带到另一种流体中。 (a) 本生燃烧器使用可调节的气体喷嘴，吸入空气以实现正常燃烧。 (b) 雾化器使用挤压灯泡产生吸入香水滴的空气射流。油漆喷雾器和化油器使用非常相似的技术来移动各自的液体。 (c) 普通的吸气器使用高速水流来形成压力较低的区域。在牙科和外科手术中，吸气器可用作抽吸泵，或者用于排干被洪水淹没的地下室或降低容器中的压力。 (d) 热水器的烟囱设计用于将空气带入通往天花板的管道中。

速度测量

图中\(\PageIndex{4}\)显示了两个应用伯努利原理测量流体速度的设备。 (a) 部分的压力计连接到两根足够小的管道，不会明显干扰流动。面对迎面而来的流体的管道会产生一个前方速度为零（v ₁ = 0）的死点，而通过另一个管道的流体的速度为 v ₂。这意味着伯努利的原则如上所述

\[p_{1} + \frac{1}{2} \rho v_{1}^{2} = p_{2} + \frac{1}{2} \rho v_{2}^{2}\]

变成

\[p_{1} = p_{2} + \frac{1}{2} \rho v_{2}^{2} \ldotp\]

因此，第二个开口处的压力 p ₂ 降低了\(\frac{1}{2} \rho v_{2}^{2}\)，因此压力计中的流体在与第二个开口相连的一侧上升了 h，其中

\[h \propto \frac{1}{2} \rho v_{2}^{2} \ldotp\]

（回想一下，这个符号的\(\propto\)意思是 “成比例”。）求解 v ₂，我们看见了

\[v_{2} \propto \sqrt{h} \ldotp\]

第 (b) 部分显示了该设备的一个版本，该版本通常用于测量各种流体速度；此类设备经常用作飞机空速指示器。

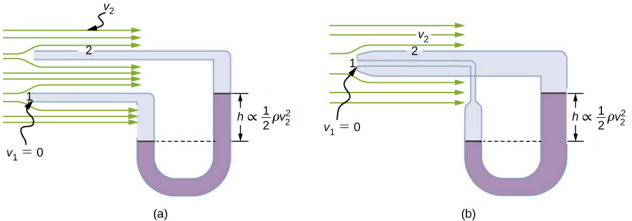
图 A 是一张压力计的图，该压力计连接到两根紧密相连的管道，并且足够小，不会干扰流动。管道 1 在面向水流的末端处于打开状态，而管道 2 的侧面有一个开口。图 B 是一张压力计的图，该压力计连接到两根管道，其中一根管（管 1）插入另一根管（管 2）中。管道 1 在面向水流的末端处于打开状态，而管道 2 的侧面有一个开口。 — 图\(\PageIndex{4}\)：根据伯努利原理测量流体速度。 (a) 压力计连接到两根紧密相连且足够小的管道，不会干扰流动。管道 1 在朝向水流的末端处于打开状态。那里会出现一个速度为零的死点。管道 2 的侧面有一个开口，因此流体穿过开口的速度为 v；因此，那里的压力会下降。压力计的压力差为\(\frac{1}{2} \rho v_{2}^{2}\)，所以 h 与成正比\(\frac{1}{2} \rho v_{2}^{2}\)。 (b) 这种类型的速度测量设备是普朗特管，也称为皮托管。

消防水带

伯努利方程的所有前述应用都涉及简化条件，例如恒定高度或恒定压力。下一个例子是伯努利方程的更通用应用，其中压力、速度和高度都发生变化。

示例 14.7：计算压力-消防水带喷嘴

用于重大结构火灾的消防水带的内径为 6.40 cm（图\(\PageIndex{5}\)）。假设这样的软管的流量为 40.0 L/s，起始表压为 1.62 x 10 ⁶ N/m ²。软管沿梯子上升 10.0 m，通向内径为 3.00 cm 的喷嘴。喷嘴中的压力是多少？

该图是带有加长梯子的消防车的绘图。梯子顶部的消防员使用软管灭火。来自软管的水流与地面平行，位于地面上方 10 米处。 — 图\(\PageIndex{5}\)：该消防水带喷嘴中的压力低于地面压力，原因有两个：水必须上坡才能到达喷嘴，喷嘴速度加快。尽管压力降低了，但水凭借其动能，可以对它击中的任何东西施加很大的力。一旦水流进入空气，其中的压力就会等于大气压力。

策略

我们必须使用伯努利方程来求解压力，因为深度不是恒定的。

解决方案

伯努利方程为

\[p_{1} + \frac{1}{2} \rho v_{1}^{2} + \rho gh_{1} = p_{2} + \frac{1}{2} \rho v_{2}^{2} + \rho gh_{2} \nonumber \]

其中，下标 1 和 2 分别指地面的初始条件和喷嘴内部的最终条件。我们必须首先找到速度 v ₁ 和 v ₂。由于 Q = A ₁ v ₁，我们得到

\[v_{1} = \frac{Q}{A_{1}} = \frac{40.0 \times 10^{-3}\; m^{3}/s}{\pi (3.20 \times 10^{-2}\; m)^{2}} = 12.4\; m/s \ldotp \nonumber\]

同样，我们发现

\[v_{2} = 56.6\; m/s \ldotp \nonumber\]

这种相当大的速度有助于到达火源。现在，将 h ₁ 设为零，我们求解 p ₂ 的伯努利方程：

\[p_{2} = p_{1} + \frac{1}{2} \rho (v_{1}^{2} - v_{2}^{2}) - \rho gh_{2} \ldotp \nonumber\]

替换已知值会产生

\[\begin{align*} p_{2} & = (1.62 \times 10^{6}\; N/m^{2}) + \frac{1}{2} (1000\; kg/m^{3}) [(12.4\; m/s)^{2} - (56.6\; m/s)^{2}] - (1000\; kg/m^{3})(9.80\; m/s^{2})(10.0\; m) \\ & = 0 \ldotp \end{align*}\]

意义

该值是表压，因为初始压力是以表压形式给出的。因此，喷嘴压力必须等于大气压力，因为水流入大气时其条件不会发生变化。