14.7: 流体动力学

Last updated
Save as PDF

Page ID: 205073

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

描述流量的特征
计算流速
描述流速和速度之间的关系
解释连续性方程对质量守恒的影响

本章的第一部分涉及流体静力学，即静态液体的研究。本章的其余部分涉及流体动力学，即对运动流体的研究。即使是最基本的流体运动形式也可能非常复杂。出于这个原因，我们在许多例子中将研究局限于理想的液体。理想的流体是粘度可以忽略不计的流体。粘度是衡量流体内部摩擦力的指标；我们在《粘度和湍流》中对其进行了更详细的研究。在几个例子中，我们研究了一种不可压缩的流体，这种流体需要极大的力才能改变体积，因为不可压缩流体中的密度在整个过程中都是恒定的。

流量特征

速度矢量通常用于说明气象学等应用中的流体运动。例如，风（空气在大气中的流体运动）可以用表示地图上任何给定点的风速和方向的矢量来表示。该图$\PageIndex{1}$显示了描述2014年亚瑟飓风期间风速矢量。

图为亚瑟飓风沿东海岸行进的压力图。低压中心用蓝点表示。低压中心附近的风速最高，风沿逆时针方向围绕低压中心移动。 — 图$\PageIndex{1}$：速度矢量显示亚瑟飓风中的风流。注意飓风眼睛周围的风向循环。眼睛附近的风速最高。颜色代表相对涡度，是衡量空气转动或旋转的指标。

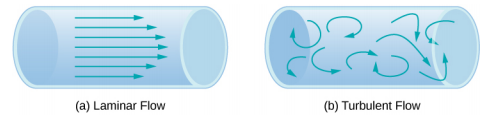
另一种表示流体运动的方法是流线型。流线表示少量流体流动时的路径。速度始终与流线相切。图中的图表$\PageIndex{2}$使用流线来说明流体在管道中移动的两个示例。第一种流体呈现层流（有时被描述为稳定的流动），以平滑的平行流线表示。请注意，在 (a) 部分所示的示例中，由于流体的粘度以及管壁与流体之间的摩擦力，流体在中心的速度最大，而在管壁附近的速度会降低。这是层流的特例，在这种情况下，管道和流体之间的摩擦力很高，被称为无滑动边界条件。第二张图表示湍流，其中的流线是不规则的，并且会随着时间的推移而变化。在湍流中，流体流动的路径是不规则的，因为流体的不同部分混合在一起或形成类似于漩涡的小圆形区域。当流体的速度达到一定的临界速度时，就会发生这种情况。

图 A 是层流示意图，显示为流体层以平行线移动。图 B 是湍流示意图，显示为流体层在不规则的碰撞路径中移动。 — 图$\PageIndex{2}$：(a) 层流可以看作是以平行规则路径移动的流体层。 (b) 在湍流中，流体区域以不规则的碰撞路径移动，导致混合和旋转。

流速及其与速度的关系

在一段时间内通过给定位置通过某个区域的流体体积称为流速$Q$，或者更确切地说是体积流量。在符号中，这写成

\[Q = \frac{dV}{dt} \label{14.13}\]

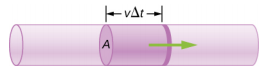
其中$V$是音量，$t$是经过的时间。在图中$\PageIndex{3}$，气缸的体积是$Ax$，所以流量是

\[Q = \frac{dV}{dt} = \frac{d}{dt} (Ax) = A \frac{dx}{dt} = Av \ldotp\]

流速的 SI 单位为 m ³ /s，但常用的其他几个单位，例如升/分钟 (L/min)。$Q$ 请注意，升 (L) 等于 1/1000 立方米或 1000 立方厘米（10 ⁻³ m ³ 或 10 ³ cm ³）。

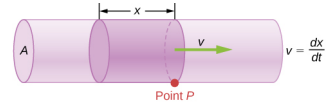
图为横截面积为 A 的均匀管道示意图。流体流过管道。流体 V 的体积 V 在时间 t 中经过一个点 P。 — 图$\PageIndex{3}$：流速是单位时间内流过某个点的流$A$体量。在这里，阴影的流体圆柱体在均匀的管道$P$中及时流过点$t$。

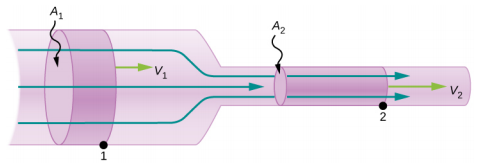
流速和速度是相互关联的，但完全不同的物理量。为了明确区别，请考虑河流的流量。水的速度越大，河流的流速越大。但是流速也取决于河流的大小和形状。例如，一条快速的山间溪流输送的水远少于巴西的亚马逊河。该图$\PageIndex{3}$说明了体积流速。体积流速为$Q = \frac{dV}{dt} = Av$，其中 A 是管道的横截面积，v 是速度的大小。

流量和平均速度之间的精确关系$v$是$Q$

\[Q = Av,\]

其中$A$是横截面积，$v$是平均速度。这种关系告诉我们，流速与流体的平均速度和河流、管道或其他管道的横截面积成正比。导管越大，其横截面积越大。该图$\PageIndex{3}$说明了如何获得这种关系。阴影圆柱体有一个体积$V = Ad$，它在一定时间$P$内流过该点$t$。将这种关系的两边除以 g$t$ ives

\[\frac{V}{t} = \frac{Ad}{t} \ldotp \label{eq14.14A} \]

我们注意到$Q = \frac{V}{t}$，平均速度是$v = \frac{d}{t}$。因此，方程\ ref {eq14.14a} 变成了

\[Q = Av.\]

图中$\PageIndex{4}$显示了沿着半径减小的管道流动的不可压缩流体。由于流体是不可压缩的，因此必须有相同数量的流体在给定时间内流过管道中的任何点，以确保流动的连续性。流量是连续的，因为它们不是增加或移除质量的源头或汇点，因此流入管道的质量必须等于流出管道的质量。在这种情况下，由于管道的横截面积减小，因此速度必须增加。这种逻辑可以扩展为管道上所有点的流速必须相同。特别是，对于任意点 1 和 2

\[\begin{split} Q_{1} & = Q_{2}, \\ A_{1} v_{1} & = A_{2} v_{2} \ldotp \end{split} \label{14.14}\]

这称为连续性方程，适用于任何不可压缩的流体（密度恒定）。当水从软管流入狭窄的喷嘴时，可以观察到连续性方程的后果：水以很快的速度出现，这正是喷嘴的目的。相反，当河流排入水库的一端时，水会大大减速，当它离开水库的另一端时，速度可能会再次加快。换句话说，当横截面积减小时，速度会增加，而当横截面积增加时，速度会降低。

图为从横截面区域 A1 缩小到横截面区域 A2 的管线示意图。流体流过管道。在时间 t 中，流体 V1 的体积通过位于宽横截面部分的点 1。流体 V2 的体积在时间 t 中通过位于狭窄横截面部分的点 2。 — 图$\PageIndex{4}$：当管子变窄时，相同体积占用的长度更大。要使相同的音量在给定时间内通过点 1 和 2，在点 2 处的速度必须更大。这个过程是完全可逆的。如果流体朝相反方向流动，则管道变宽时其速度会降低。（请注意，两个圆柱体的相对体积和相应的速度向量箭头不是按比例绘制的。）

由于液体本质上是不可压缩的，因此连续性方程对所有液体都有效。但是，气体是可压缩的，因此，如果气体受到压缩或膨胀，则必须谨慎使用方程式。

示例 14.5：计算通过喷嘴的流体速度

直径为 0.500 cm 的喷嘴连接到半径为 0.900 cm 的花园软管上。通过软管和喷嘴的流速为 0.500 L/s。计算水的速度：

在软管里和
在喷嘴里。

策略

我们可以利用流速和速度之间的关系来找到两种速度。我们使用下标 1 表示软管，2 表示喷嘴。

解决方案

我们求解速度和软管横截面积的流速方程，得出 $$v =\ frac {Q} {A} =\ frac {Q} {\ pi r_ {1} ^ {2}}\ ldotp$$ 替换值并使用适当的单位转换得出 $$v =\ frac {(0.500\; L/s) (10^ {-3}\; m^ 3} /L)} {(3.14) (9.00\ times 10^ {-3}\; m) ^ {2}$\pi r_{1}^{2}$} = 1.96\; m/s\ ldotp$$
我们可以重复这个计算来找出喷嘴 v ₂ 中的速度，但是我们使用连续性方程来给出略有不同的洞察力。方程表示 $$A_ {1} v_ {1} = A_ {2} v_ {2}\ ldotp$求解 v ₂ 然后用横截面积代替$\pi r^{2}$ $v_ {2} =\ frac {A_ {1}} {A_ {1}} =\ frac {\ pi r_ {1} ^ {2}} {\ pi r_ {2} ^ {2}} v_ {1} =\ frac {r_ {1} ^ {2}} {r_ {2} ^ {2}} v_ {1}\ ldotp$$ 替换已知值，$$v_ {2} =\frac {(0.900\; cm) ^ {2}} {(0.250\; cm) ^ {2}} (1.96\; m/s) = 25.5\; m/s\ ldotp$$

意义

1.96 m/s 的速度对于从没有喷嘴的软管中流出的水来说差不多。仅通过将流量限制到较窄的管道中，喷嘴就会产生更快的流量。

示例最后一部分的解表明，速度与管道半径的平方成反比，当半径变化时效果很大。我们可以在很远的距离吹出蜡烛，比如说，通过张开嘴唇，而张开嘴巴吹蜡烛是相当无效的。

大众保护

流体的流速也可以用质量流速或质量流速来描述。这是大量流体移动到某一点的速率。再次参考图$\PageIndex{3}$，但这次要考虑阴影体积中的质量。质量可以通过密度和体积来确定：

\[m = \rho V = \rho Ax \ldotp\]

然后质量流速为

\[\frac{dm}{dt} = \frac{d}{dt} (\rho Ax) = \rho A \frac{dx}{dt} = \rho Av,\]

其中$\rho$是密度，A 是横截面积，v 是速度的大小。质量流速是流体动力学中的重要量，可用于解决许多问题。以图为例$\PageIndex{5}$。图中的管道从入口开始，横截面积为 A ₁，然后收缩到横截面积较小的出口 A ₂。进入管道的流体质量必须等于离开管道的流体质量。因此，出口 (v ₂) 的速度大于入口的速度 (v ₁)。利用进入管道的流体质量必须等于流出管道的流体质量这一事实，我们可以通过计算质量输入和质量流出的变化率来找到速度和横截面积之间的关系：

\[\begin{split} \left(\dfrac{dm}{dt}\right)_{1} & = \left(\dfrac{dm}{dt}\right)_{2} \\ \rho_{1} A_{1} v_{1} & = \rho_{2} A_{2} v_{2} \ldotp \end{split} \label{14.15}\]

方程\ ref {14.15} 也被称为一般形式的连续性方程。如果流体的密度在收缩过程中保持恒定（即流体不可压缩），则密度将从连续性方程中抵消，

\[A_{1} v_{1} = A_{2} v_{2} \ldotp\]

方程缩小后显示进入管道的体积流速等于流出管道的体积流量。

图为流体在均匀管道中流动的示意图，其横截面积为 A。在 delta t 期间，流体体积 V delta t 通过管道。 — 图$\PageIndex{5}$：用于推导连续性方程的几何。如果液体不可压缩，进入横截面（阴影）区域的液体量必须等于离开横截面积的液体量。