14.6: 阿基米德原理和浮力

Last updated
Save as PDF

Page ID: 205080

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

定义浮力
国家阿基米德的原则
描述密度与阿基米德原理之间的关系

当放置在流体中时，一些物体由于浮力而漂浮。这种浮力从何而来？为什么有些东西会漂浮而另一些不会？沉没的物体会从流体中得到任何支撑吗？你的身体受到大气层的鼓舞，还是只有氦气球受到影响（图\(\PageIndex{1}\)）？

图 A 是一幅淹没在水下的船锚的画，旁边是一些海灌木。图 B 是一艘浮动潜水艇的照片，三面都有尾流。图 C 是漂浮在空中的许多彩色气球的照片。 — 图\(\PageIndex{1}\)：（a）即使是沉没的物体，比如这个锚，在淹没时也会部分地由水支撑。 (b) 潜艇的密度可调（压载舱），因此可以根据需要漂浮或沉没。 (c) 充满氦气的气球向上拉动绳子，展示了空气的浮力效果。（来源 b：修改盟军的作品；来源 c：“Crystl” /Flickr 对作品的修改）

所有这些问题以及许多其他问题的答案都基于这样一个事实，即压力会随着流体深度的增加而增加。这意味着流体中对象底部的向上力大于对象顶部的向下力。任何流体中的任何物体都有向上力或浮力（图\(\PageIndex{2}\)）。如果浮力大于物体的重量，则物体上升到表面并漂浮。如果浮力小于物体的重量，则物体会下沉。如果浮力等于物体的重量，则该物体可以在其当前深度保持悬浮状态。无论物体漂浮、下沉还是悬浮在流体中，浮力始终存在。

浮力

浮力是指任何流体中任何物体上的向上力。

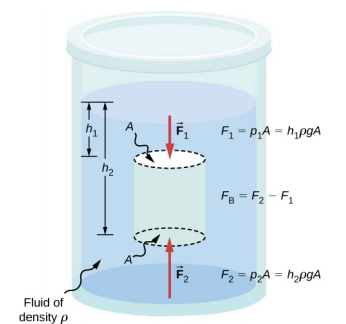
该图是装满液体并一侧向大气开口的圆柱体的示意图。表面积 A 小于圆柱体表面积的虚构物体被浸入流体中。流体顶部和物体顶部之间的距离为 h1。流体顶部和物体底部之间的距离为 h2。力 F1 和 F2 分别施加到物体的顶部和底部。 — 图\(\PageIndex{2}\)：流体重量引起的压力会随着深度的增加而增加，因为\(p = h \rho g\)。压力的这种变化以及气缸底部的相关向上力大于气缸顶部的向下力。力的差异会产生浮力 F _B。（水平力取消。）

阿基米德原理

浮力到底有多大？要回答这个问题，请考虑一下当水下物体从流体中移除时会发生什么，如图所示\(\PageIndex{3}\)。如果物体不在流体中，则该物体占据的空间将由重量为 w _fl 的流体填充。该重量由周围的流体支撑，因此浮力必须等于 w _fl，即被物体移位的流体的重量。

阿基米德原理

物体上的浮力等于它置换的流体的重量。在方程形式中，阿基米德的原理是

\[F_{B} = w_{fl},\]

其中 F _B 是浮力，w _fl 是被物体移位的流体的重量。

这个原理以希腊数学家和发明家阿基米德（约公元前287—212年）命名，他在武力概念确立之前很久就阐述了这一原理。

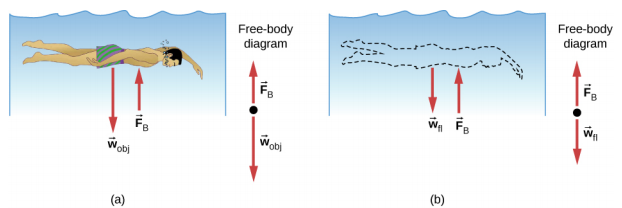
图 A 是一幅被水淹没的人的画。 Force wobj 由人表达，力 Fb 由水对人施加。图 B 是一幅用水代替人物的图。现在 Force wfl 由取代人的水来表达，force Fb 保持不变。 — 图\(\PageIndex{3}\)：(a) 浸入流体中的物体会受到浮力 F _B。如果 F _B 大于物体的重量，则物体升高。如果 F _B 小于物体的重量，则物体下沉。 (b) 如果物体被移除，则取而代之的是重量为 w _fl 的液体。由于该重量由周围流体支撑，因此浮力必须等于移位流体的重量。

阿基米德的原理是指当人体部分或全部浸入液体中时产生的浮力。提供流体压力的力作用在垂直于身体表面的身体上。换句话说，由底部压力产生的力指向上方，而在顶部，压力产生的力指向下方；侧面压力产生的力指向身体。

由于身体底部的深度大于身体顶部的深度，因此身体下部的压力高于上部的压力，如图所示\(\PageIndex{2}\)。因此，净向上的力作用在身体上。这种向上的力量是浮力的力，或者仅仅是浮力。

惊叹号 “尤里卡”（意思是 “我找到了”）经常被归功于阿基米德，因为他发现了将导致阿基米德原理的发现。有人说这一切都是从浴缸里开始的。要阅读这个故事，请浏览《科学美国人》以了解更多信息。

密度和阿基米德原理

如果你把一块粘土丢进水里，它就会沉没。但是，如果你将同样的粘土块塑造成船的形状，它就会漂浮。由于其形状，尽管其质量相同，但粘土船排出的水比块多，并且承受的浮力更大。钢船也是如此。

物体的平均密度最终决定了它是否漂浮。如果物体的平均密度小于周围流体的平均密度，它将漂浮。原因是流体密度更高，在相同体积下含有更多的质量，因此重量也更大。因此，浮力等于移位流体的重量，大于物体的重量。同样，密度大于流体的物体也会下沉。

浮动物体被淹没的程度取决于该物体的密度与流体密度的比较情况。例如\(\PageIndex{4}\)，在图中，与装载时的同一艘船相比，卸载的船的密度较低，被淹没的船只也更少。通过考虑密度，我们可以得出淹没部分的定量表达式。淹没的分数是浸入的体积与物体体积的比率，或

\[fraction\; submerged = \frac{V_{sub}}{V_{obj}} = \frac{V_{fl}}{V_{obj}} \ldotp\]

浸没的体积等于排出的液体量，我们称之为 V _fl。现在我们可以通过代\(\rho = \frac{m}{V}\)入表达式来获得密度之间的关系。这给了

\[\frac{V_{fl}}{V_{obj}} = \frac{\frac{m_{fl}}{\rho_{fl}}}{\frac{m_{obj}}{\rho_{obj}}},\]

其中\(\rho_{obj}\)是物体的平均密度，\(\rho_{fl}\)是流体的密度。由于物体漂浮，因此其质量和位移流体的质量相等，因此它们从方程中抵消，留下

\[fraction\; submerged = \frac{\rho_{obj}}{\rho_{fl}} \ldotp\]

我们可以使用这种关系来测量密度。

图 A 是一张漂浮在水中的卸载船只的图。图 B 是一张漂浮在水深处的满载船只的图。 — 图\(\PageIndex{4}\)：卸载的船只（a）比装载的船只（b）在水中漂浮得更高。

示例 14.4：计算平均密度

假设一个体重为60.0公斤的女性在肺部充满空气时漂浮在淡水中，其体积的97.0％被淹没。她的平均密度是多少？

策略

我们可以通过求解方程找到女人的密度

\[fraction\; submerged = \frac{\rho_{obj}}{\rho_{fl}}\]

表示物体的密度。这会产生

\[\rho_{obj} = \rho_{person} = (fraction\; submerged) \cdotp \rho_{fl} \ldotp\]

我们知道水中的分数和水的密度，因此我们可以计算出女性的密度。

解决方案

在她的密度表达式中输入已知值，我们得到

\[\rho_{person} = 0.970 \cdotp 10^{3}\; kg/m^{3} = 970\; kg/m^{3} \ldotp\]

意义

女性的密度小于流体密度。我们预计会这样，因为她会漂浮。

许多低密度物体或物质漂浮在高密度的液体中：水上油、大气中的热气球、葡萄酒中的软木塞、盐水中的冰山以及 “熔岩灯” 中的热蜡等。一个不太明显的例子是山脉漂浮在密度较高的地壳上，地幔位于它们之下。即使看似坚固的地球也具有流体特性。

测量密度

确定密度的最常用技术之一如图所示\(\PageIndex{5}\)。

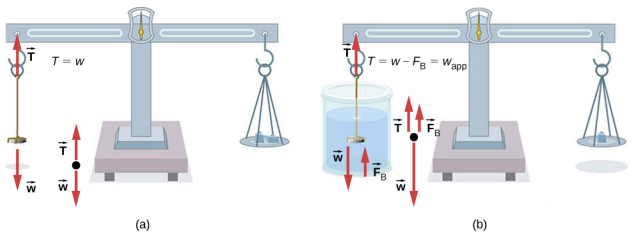
图 A 是一幅用手动秤称重的空中硬币的画作。大额余额用于抵消硬币。图 B 是用手动秤称重的水中同一枚硬币的画作。较小的余额用于抵消硬币。 — 图\(\PageIndex{5}\)：（a）一枚硬币在空中称重。 (b) 硬币的表观重量是在硬币完全浸入已知密度的液体中时确定的。这两个测量值用于计算硬币的密度。

物体，这里是硬币，在空气中称重，然后在浸入液体中时再次称重。如果已知流体密度，则可以计算出硬币的密度，这是其真实性的标志。如果硬币的密度已知，我们可以使用同样的技术来确定流体的密度。

所有这些计算都基于阿基米德原理，该原理指出，物体上的浮力等于移位流体的重量。反过来，这意味着物体在水下时重量会减轻；我们称这种测量值为物体的表观重量。物体的明显重量减轻等于排出的液体的重量。或者，在测量质量的天平上，物体遭受的明显质量损失等于移位的流体质量。也就是说，表观的重量减轻等于排出的液体的重量，或者表观质量损失等于排出的液体质量。