14.5: 帕斯卡原理和液压系统

学习目标

• 陈述帕斯卡原理
• 描述帕斯卡原理的应用
• 推导液压系统中力之间的关系

1653年，法国哲学家和科学家布莱斯·帕斯卡（Blais e Pascal）发表了他的《液体平衡论文》，他在论文中讨论了静态流体的原理。 静态流体是一种不运动的流体。 当流体不流动时，我们说流体处于静态平衡。 如果流体是水，我们说它处于静水平衡状态。 对于处于静态平衡状态的流体，流体任何部分上的净力必须为零；否则流体将开始流动。

帕斯卡的观测结果——自实验证明——为水力学奠定了基础，液压是现代机械技术最重要的发展之一。 帕斯卡观察到，施加在封闭流体上的压力的变化不会减弱地传递到整个流体及其容器的壁上。 因此，我们通常比流体中的其他物理量更了解压力。 此外，帕斯卡原理意味着流体中的总压力是来自不同来源的压力的总和。 一个很好的例子是，某个深度的流体取决于流体的深度和大气的压力。

帕斯卡原理

帕斯卡原理（也称为帕斯卡定律）指出，当对封闭流体施加压力变化时，压力变化不会减弱地传递到流体的所有部分及其容器的壁上。 在封闭的流体中，由于流体的原子可以自由移动，它们将压力传递到流体的所有部分和容器的壁上。 压力的任何变化都不会减弱传播。

请注意，这个原理并不是说流体所有点的压力都是相同的，事实并非如此，因为地球附近流体中的压力随高度而变化。 相反，这个原则适用于压力的变化。 假设您在高度为 H、横截面积为 A 的圆柱形容器中放入一些水，该容器具有质量为 m 的可移动活塞（图\(\PageIndex{1}\)）。 增加活塞顶部的重量 Mg 会增加顶部的压力\(\frac{Mg}{A}\)，因为额外的重量也会作用于盖子的区域 A：

\[\Delta p_{top} = \frac{Mg}{A} \ldotp\]

图\(\PageIndex{1}\)：当流体被压缩时，流体中的压力会发生变化。 (a) 流体顶层的压力不同于底层的压力。 (b) 通过增加活塞重量而增加的压力在任何地方都是一样的，例如 p t _o p ne _w − p top = _p bott _om ne _w − p bott _om。

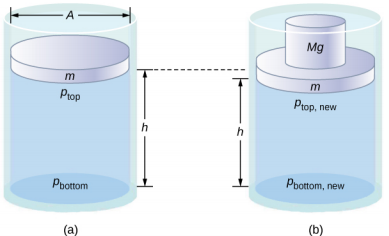
根据帕斯卡原理，水中所有点的压力变化量相同\(\frac{Mg}{A}\)。 因此，底部的压力也增加\(\frac{Mg}{A}\)了。 容器底部的压力等于大气压力、流体产生的压力和质量提供的压力的总和。 由于质量的影响，容器底部的压力变化为

\[\Delta p_{bottom} = \frac{Mg}{A} \ldotp\]

由于流体中所有地方的压力变化都相同，因此我们不再需要下标来指定顶部或底部的压力变化：

\[\Delta p = \Delta p_{top} = \Delta p_{bottom} = \Delta p_{everywhere} \ldotp\]

模拟

Pascal's Barrel 很好地体现了帕斯卡的原理。 观看 Pascal 1646 年实验的模拟，他在实验中演示了流体中压力变化的影响。

帕斯卡原理和液压系统的应用

液压系统用于操作汽车制动器、液压千斤顶和许多其他机械系统（图\(\PageIndex{2}\)）。

图\(\PageIndex{2}\)：一个典型的液压系统，有两个充有液体的气缸，上面装有活塞，并由称为液压管路的管道连接。 左活塞\(\vec{F}_{1}\)上的向下力会产生压力的变化，这种变化不会减弱地传递到封闭流体的所有部分。 这会导致右活塞\(\vec{F}_{2}\)上的向上力大于\(\vec{F}_{1}\)因为右活塞的表面积更大。

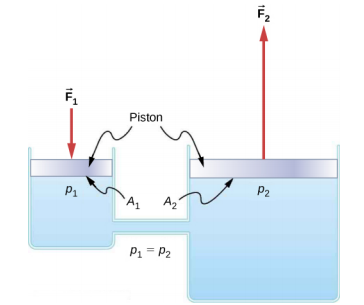
我们可以通过应用帕斯卡原理推导出这个简单液压系统中的力之间的关系。 首先要注意，系统中的两个活塞高度相同，因此由于深度不同，压力没有差异。 作用于区域 A ₁ 的 F ₁ 产生的压力很简单

\(p_{1} = \frac{F_{1}}{A_{1}}\)，定义为\(p = \frac{F}{A}\)。

根据帕斯卡的原理，这种压力在整个流体和容器的所有壁上传递不减弱。 因此，在另一个活塞处感受到的压力 p ₂ 等于 p ₁。 也就是说，p ₁ = p ₂。 但是，由于 p ₂ =\(\frac{F_{2}}{A_{2}}\)，我们可以看到

\[\frac{F_{1}}{A_{1}} = \frac{F_{2}}{A_{2}} \ldotp \label{14.12}\]

该方程将任何液压系统中的力与面积之比联系起来，前提是活塞处于相同的垂直高度并且系统中的摩擦力可以忽略不计。

液压系统可以增加或减少施加在它们上的力。 为了使力变大，将压力施加到更大的区域。 例如，如果在图 14.16 中向左气缸施加 100-N 的力，而右侧气缸的面积大五倍，则输出力为 500 N。液压系统类似于简单的杠杆，但它们的优点是压力可以通过曲折的曲线传递到几个立刻放置。

液压千斤顶就是这样的液压系统。 液压千斤顶用于举起重物，例如汽车修理工用来抬起汽车的负载。 它由 U 形管中的不可压缩流体组成，两侧都装有可移动的活塞。 U 型管的一侧比另一侧窄。 在小区域施加小力可以平衡另一侧在较大区域上施加的更大力（图\(\PageIndex{3}\)）。

图\(\PageIndex{3}\)：(a) 液压千斤顶的工作原理是使用管道两侧的可移动活塞（A ₁、A ₂）对 U 形管中的不可压缩流体施加力（F ₁、F ₂）。 (b) 汽车修理工通常使用液压千斤顶来提升车辆，以便进行维修和保养。

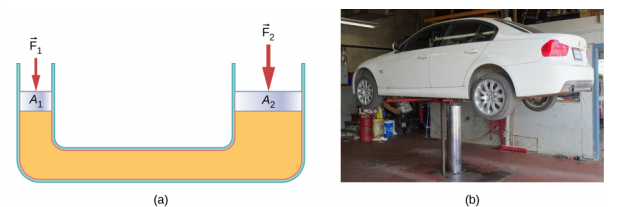
根据帕斯卡原理，可以证明提升汽车所需的力小于汽车的重量：

\[F_{1} = \frac{A_{1}}{A_{2}} F_{2},\]

其中 F ₁ 是用于提升汽车的力，A ₁ 是较小活塞的横截面积，A ₂ 是较大活塞的横截面积，F ₂ 是汽车的重量。

示例\(\PageIndex{1}\): Calculating Force on Wheel Cylinders: Pascal Puts on the Brakes

以图中所示的汽车液压系统为例\(\PageIndex{4}\)。 假设对制动踏板施加了 100 N 的力，制动踏板通过杠杆作用于踏板缸（作为 “主” 缸）。 500 N 的力施加在踏板缸上。 在踏板缸中产生的压力被传递到四轮气缸。 踏板缸的直径为 0.500 厘米，每个车轮缸的直径为 2.50 厘米。 计算在每个车轮缸上产生的力 F ₂ 的大小。

图\(\PageIndex{4}\)：液压制动器使用帕斯卡原理。 驾驶员按下制动踏板，施加的力通过简单的杠杆增加，然后通过液压系统再次增加。 每个相同的轮缸承受相同的压力，因此产生相同的力输出 F ₂。 踏板和车轮缸的圆形横截面积分别由 A ₁ 和 A ₂ 表示

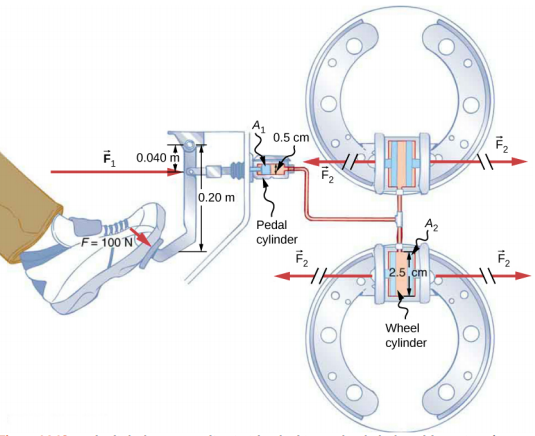
策略

我们被赋予了施加在踏板缸上的力 F ₁。 横截面积 A ₁ 和 A ₂ 可以根据它们的给定直径计算。 然后我们可以使用以下关系来找到力 F ₂：

\[\frac{F_{1}}{A_{1}} = \frac{F_{2}}{A_{2}} \ldotp\]

以代数方式对其进行操作，使一侧获得 F ₂ 并替换已知值。

解决方案

Pascal 应用于液压系统的原理如下所示\(\frac{F_{1}}{A_{1}} = \frac{F_{2}}{A_{2}}\)：

\[\begin{split} F_{2} & = \frac{A_{2}}{A_{1}} F_{1} = \frac{\pi r_{2}^{2}}{\pi r_{1}^{2}} F_{1} \\ & = \frac{(1.25\; cm)^{2}}{(0.250\; cm)^{2}} \times 500\; N = 1.25 \times 10^{4}\; N \ldotp \end{split}\]

意义

该值是四个轮缸中每个气缸所施加的力。 请注意，我们可以根据需要添加任意数量的轮缸。 如果每个液压系统的直径为 2.50 厘米，则每个系统将施加 1.25 x 10 ⁴ N。以简单机器为例，简单的液压系统可以增加力，但不能做比在其上所做的更多的工作。 工作是力乘以移动距离，轮缸的移动距离小于踏板气缸的距离。 此外，添加的轮子越多，每个轮子移动的距离就越小。 许多液压系统（例如动力制动器和推土机中的液压系统）都有电动泵，该泵实际上可以完成系统中的大部分工作。

练习\(\PageIndex{1}\)

如果使用气体代替液体，液压机还能正常运行吗？