14.4: 测量压力

Last updated
Save as PDF

Page ID: 205065

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

定义表压和绝对压力
解释测量压力的各种方法
了解开管气压计的工作原理
详细描述压力计和气压计的工作原理

在上一节中，我们得出了一个用于计算处于静水平衡状态的流体压力变化的公式。事实证明，这是一个非常有用的计算。压力测量在日常生活以及科学和工程应用中都很重要。在本节中，我们将讨论报告和测量压力的不同方法。

表压与绝对压力

假设装满的潜水箱上的压力表读数为 3000 psi，即大约 207 个大气压。当阀门打开时，空气开始逸出，因为储罐内部的压力大于储罐外的大气压力。空气继续从储罐中排出，直到储罐内的压力等于储罐外大气的压力。此时，储罐上的压力表读数为零，尽管储罐内部的压力实际上为 1 个大气压——与储罐外部的气压相同。

大多数压力表，例如潜水箱上的压力表，都经过校准，可以在大气压下读取零。来自此类仪表的压力读数称为表压，即相对于大气压力的压力。当储罐内的压力大于大气压力时，压力表会报告正值。有些仪表是为测量负压而设计的。例如，许多物理实验必须在真空室中进行，真空室是从中抽出一些空气的刚性腔室。真空室内的压力小于大气压力，因此真空室上的压力表读取负值。与表压不同，绝对压力是指大气压力，这实际上会增加未封闭在刚性容器中的任何流体的压力。

定义绝对压力

绝对压力或总压力是表压和大气压之和：

\[p_{abs} = p_{g} + p_{atm} \label{14.11}\]

其中 p _abs 是绝对压力，p _g 是表压，p _atm 是大气压力。

例如，如果轮胎压力表读数为 34 psi，则绝对压力为 34 psi 加 14.7 psi（以 psi 为单位 p _atm）或 48.7 psi（相当于 336 kPa）。

在大多数情况下，流体中的绝对压力不能为负。流体推动而不是拉动，因此流体中最小的绝对压力为零（负绝对压力是拉力）。因此，可能的最小表压为 p _g = −p _atm（这使得 p _abs 为零）。表压的大小没有理论上的限制。

测量压力

许多设备用于测量压力，从轮胎仪表到血压监视器不等。许多其他类型的压力表通常用于测试流体的压力，例如机械压力表。在本节中，我们将探讨其中的一些内容。

任何以已知方式随压力变化的属性都可用于构造压力表。一些最常见的类型包括应变计，它使用材料的形状随压力的变化；电容压力表，它使用形状随压力变化而产生的电容变化；压电压力表，它在压电两端产生电压差两侧之间存在压差的材料；以及离子计，通过在高度真空腔中对分子进行电离来测量压力。不同的压力表在不同的压力范围和不同的物理环境下很有用。一些例子如图所示$\PageIndex{1}$。

图 A 是用于监测气瓶压力的仪表的照片。图 B 是轮胎压力表的照片。图 C 是用于监测真空系统压力的电离计的照片。 — 图$\PageIndex{1}$：(a) 仪表用于测量和监测气瓶中的压力。压缩气体用于许多工业和医疗应用。 (b) 轮胎压力表有许多不同的型号，但都用于相同的目的：测量轮胎的内部压力。这使驾驶员能够在负载重量和驾驶条件下保持轮胎在最佳压力下充气。 (c) 电离计是一种高灵敏度设备，用于监测封闭系统中气体的压力。中性气体分子通过电子的释放被电离化，电流被转换为压力读数。电离计通常用于依赖真空系统的工业应用。

压力计

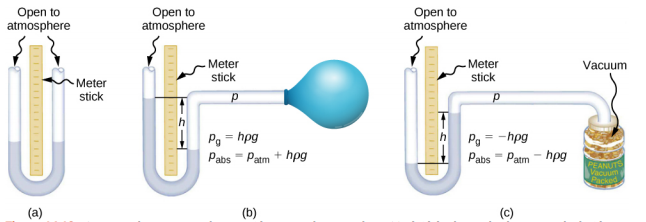
最重要的压力表类别之一采用这样的特性，即由恒定密度流体的重量产生的压力由 p = h$\rho$ g 给出。图中所示的 U 形管$\PageIndex{2}$是压力计的示例；在 (a) 部分，管的两侧都向压力计开放大气层，允许两侧的大气压力平均向下推动，从而抵消其影响。

只有一侧向大气开口的压力计是测量表压力的理想设备。表压为 p _g = h$\rho$ g，通过测量 h 得出。例如，假设 U 型管的一侧连接到某个压力源 p _abs，例如图 (b) 部分中的气球或 (c) 部分所示的真空包装的花生罐。压力不减地传递到压力计，液位不再相等。在 (b) 部分中，p _abs 大于大气压力，而在 (c) 部分中，pabs 小于大气压力。在这两种情况下，p _abs 与大气压的差异均为 h$\rho$ g，其中$\rho$是压力计中流体的密度。在 (b) 部分中，p _abs 可以支撑一列高度为 h 的液体，因此它施加的压力 h$\rho$ g 必须大于大气压（表压 p _g 为正）。在 (c) 部分中，大气压力可以支撑高度为 h 的液体，因此 p _abs 比大气压小一量 h$\rho$ g（表压 p _g 为负）。

图 A 是两侧都向大气开放的开管压力计的示意图。两侧的水位高度相同。图 B 是开管压力计的示意图，该压力计的一侧向大气开放，另一侧与气球相连。通往大气的一侧的水位更高。图 C 是开管压力计的示意图，该压力计的一侧向大气开放，另一侧与一罐真空包装的花生相连。通往大气的一侧的水位较低。 — 图$\PageIndex{2}$：开管压力计的一侧向大气开放。 (a) 两侧的流体深度必须相同，否则两侧在底部施加的压力将不相等，液体将从更深的一侧流出。 (b) 传递到压力计一侧的正表压 p _$\rho$g = h g 可以支撑一列高度为 h 的液体。(c) 同样，大气压力比负表压 p _g 大一量 h$\rho$ g。罐子的刚性会阻碍大气层压力传递给花生。

气压计

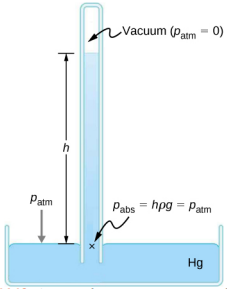
压力计通常使用液体（通常是汞）的 U 形管来测量压力。 气压计（图$\PageIndex{3}$）是一种通常使用单列汞来测量大气压的设备。该晴雨表由意大利数学家和物理学家伊万格丽斯塔·托里切利（1608—1647 年）于 1643 年发明，由一端封闭并充满水银的玻璃管构成。然后将管子倒置并放入水银池中。该设备测量大气压力，而不是表压，因为在管道中的汞上方有一个几乎纯净的真空。水银的高度使得 h$\rho$ g = p _atm。当大气压力变化时，汞升高或下降。

天气预报员密切监测大气压力的变化（通常报告为气压），因为汞升高通常表示天气改善，汞下降表示天气恶化。气压计也可以用作高度计，因为平均大气压随海拔高度而变化。水银气压计和压力计非常常见，以至于大气压和血压通常以毫米汞柱为单位。

水银晴雨表的示意图。由于水银上方的压力为零，因此大气能够将管道中的汞推至高度 h。 — 图$\PageIndex{3}$：水银气压计测量大气压力。水银重量产生的压力 h$\rho$ g 等于大气压力。由于水银上方的压力为零，因此大气能够将管道中的汞推至高度 h。

示例$\PageIndex{1}$: Fluid Heights in an Open U-Tube

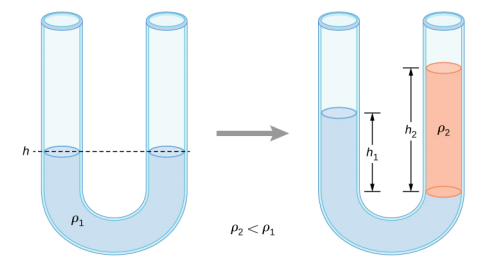
两端都打开的 U 形管在两侧填充密度$\rho_{1}$为 h 的液体（图$\PageIndex{1}$）。将密$\rho_{2} < \rho_{1}$度高的液体倒入一侧，液体 2 沉淀在液体 1 的顶部。两侧的高度不同。从界面到液体 2 顶部的高度为 h ₂，液体 1 从接口高度到顶部的高度为 h ₁。推导出高度差的公式。

左图显示了装满液体的 U 形管。 U 形管两侧的液体高度相同。右图显示了一个 U 形管，里面装有两种不同密度的液体。 U 形管两侧的液体高度不同。 — 图$\PageIndex{4}$：U 形管中显示了两种不同密度的液体。

策略

只要 U 形管两侧相同高度的点处的压力必须相同，前提是这两个点在同一个液体中。因此，我们考虑管道两臂中两个处于相同高度的点：一个点是 Liquid 2 一侧的接口，另一个点是手臂上与 Liquid 1 的点，与另一只手臂的接口处于同一高度。每个点的压力是由大气压加上其上方液体的重量造成的。

液体侧面压力 1 = p ₀ +$\rho_{1}$ gh ₁

液体侧面压力 2 = p ₀ +$\rho_{2}$ gh ₂

解决方案

由于这两个点在 Liquid 1 中并且高度相同，因此这两个点的压力必须相同。因此，我们有

\[p_{0} + \rho_{1} gh_{1} = p_{0} + \rho_{2} gh_{2} \ldotp \nonumber\]

因此，

\[\rho_{1} h_{1} = \rho_{2} h_{2} \ldotp \nonumber\]

这意味着 U 型管两侧的高度差为

\[h_{2} - h_{1} = \left(1 - \dfrac{p_{1}}{p_{2}}\right) h_{2} \ldotp \nonumber\]

如果我们设定$\rho_2 = \rho_1$，结果是有意义的，这给出 h ₂ = h ₁。如果两边密度相同，则它们的高度相同。

练习$\PageIndex{1}$

汞是一种危险物质。你为什么认为气压计中通常使用汞而不是水等更安全的液体？

压力单位

如前所述，压力的 SI 单位是帕斯卡 (Pa)，其中

\[1\; Pa = 1\; N/m^{2} \ldotp\]

除帕斯卡外，还有许多其他常用的压力单位（表$\PageIndex{1}$）。在气象学中，大气压力通常以毫巴 (mb) 为单位来描述，其中

\[1000\; mb = 1 \times 10^{5}\; Pa \ldotp\]

对于气象学家来说，毫巴是一个方便的单位，因为地球海平面上的平均大气压力为 1.013 x 10 ⁵ Pa = 1013 mb = 1 atm。使用在考虑流体深度压力时得出的方程式，压力也可以用毫米或英寸的汞来测量。在抽空顶部的容器中，在 0 °C 时，760 mm 的汞柱底部的压力等于大气压力。因此，也可以使用 760 mm Hg 代替 1 个压力气氛。在真空物理实验室中，科学家经常使用另一种叫做 torr 的装置，它以托里切利命名，正如我们刚才所见，托里切利发明了用于测量压力的水银压力计。一个 torr 等于 1 mm Hg 的压力。

表$\PageIndex{1}$：压力单位摘要
单位	定义
SI 单位：帕斯卡	$$1\; Pa = 1\; n/m^ {2} $$
英制单位：磅每平方英寸（lb/in.2 或 psi）	$$1\; psi = 7.015\ times 10^ {3}\; Pa$$
其他压力单位	$$\ begin {split} 1\; atm & = 760\; mm\; Hg\\ & = 1.013\ times 10^ {5}\; Pa\\ & = 14.7\; psi\\ & = 29.9\; 英寸\; of\; Hg\\ & = 1013\; mb\ end {split} $$
	$$1\; bar = 10^ {5}\; Pa$$
	$$1\; torr = 1\; mm\; Hg = 122.39\; Pa$$

定义绝对压力

示例\(\PageIndex{1}\): Fluid Heights in an Open U-Tube

解决方案

练习\(\PageIndex{1}\)