14.3：流体、密度和压力（第 2 部分）

Last updated
Save as PDF

Page ID: 205064

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

恒定密度流体中压力随深度的变化

压力是为所有物质状态定义的，但在讨论流体时尤其重要。流体的一个重要特征是，平行于流体表面施加的力的分量没有明显的阻力。流体的分子只需流动即可适应水平力。垂直于表面施加的力会压缩或膨胀流体。如果你尝试压缩流体，你会发现流体内部的每个点都向外产生反作用力，平衡了施加在边界分子上的力。

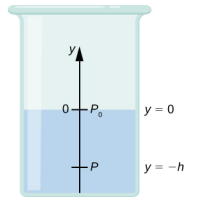
假设密度恒定的流体，如图所示$\PageIndex{1}$。容器底部的压力是由大气压力（p ₀）加上流体重量产生的压力造成的。流体产生的压力等于流体的重量除以面积。流体的重量等于其质量乘以重力引起的加速度。

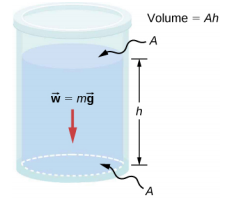
图 A 是一幅容器图。容器底部有一个区域 A。容器装满液体至高度 h。容器右侧的文字显示 “体积等于 A 乘以 h”。 — 图$\PageIndex{1}$：这个容器的底部支撑着里面液体的全部重量。垂直侧不能对流体施加向上的力（因为它无法承受剪切力），因此底部必须支撑所有流体。

由于密度是恒定的，因此可以使用密度来计算重量：

\[w = mg = \rho Vg = \rho Ahg \ldotp\]

因此，容器底部的压力等于加上流体重量的大气压除以面积：

\[p = p_{0} + \frac{\rho Ahg}{A} = p_{0} + \rho hg \ldotp\]

此方程仅适用于恒定密度流体在某个深度的压力

恒定密度流体在某深处的压力

恒定密度的流体中某个深度的压力等于大气压力加上由于流体重量而产生的压力，或

\[p = p_{0} + \rho hg, \label{14.4}\]

其中 p 是特定深度的压力，p ₀ 是大气的压力，$\rho$是流体的密度，g 是重力引起的加速度，h 是深度。

一张建在河上的大坝的照片。 — 图$\PageIndex{2}$：2008年在中国中部的长江上修建的三峡大坝建造了一个巨大的水库，导致超过一百万人流离失所。（来源：“Le Grand Portage” /Flickr）

示例 14.1：大坝必须承受什么力？

以作用在保留水库的大坝上的压力和力为例（图$\PageIndex{2}$）。假设大坝宽 500 米，水深 80.0 米，如下图所示。 (a) 水对大坝造成的平均压力是多少？ (b) 计算对大坝施加的力。

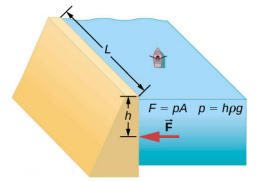
该图是河上竖立的长度为 L、高 h 的大坝的示意图。河里有一艘小型独木舟，只有一名乘客。公式 F 等于 p 乘以 A，p 等于 h 乘以 p 乘以 g。

由于水的重量而产生的平均压力 p 是平均深度 h 为 40.0 m 时的压力，因为压力随深度线性增加。水对大坝施加的力是平均压力乘以接触面积，F = pA。

解决方案

由于流体重量而产生的平均压力为 $$p = h\ rho g\ ldotp\ label {14.5} $$输入表 14.1 中的水密度并将 h 作为平均深度为 40.0 m，我们得到 $$\ begin {split} p & = (40.0\; m) (10^ {3}\; kg/m^ {3}) (9.80\; m/s^ {2})\\ & = 3.92\ times 10^ {5}\; n/m^ {2} = 392\;kPa\ ldotp\ end {split} $$
我们已经找到了 p 的值。大坝的面积为 $$A = (80.0\; m)\ times (500\; m) = 4.00\ times 10^ {4}\; m^ {2}\ ldotp$所以 $$\ begin {split} F & = (3.92\ times 10^ {5}\; n/m^ {2}) (4.00\ times 10^ {2}) (4.00\ times 10^ {4}\; m^ {2})\\ & = 1.57\ times 10^ {10}\; M\ ldotp\ end {split} $$

意义

尽管这种力看起来很大，但与水库中水的重量为1.96 x 10 ¹³ N相比，它很小。实际上，它仅为重量的0.0800％。

练习 14.1

如果示例中的水库$\PageIndex{1}$覆盖了两倍的面积，但保持在相同的深度，是否需要重新设计大坝？

均匀引力场中静态流体中的压力

静态流体是一种不运动的流体。在静态流体中的任何点，所有侧面的压力都必须相等，否则，该点的流体会对净力做出反应并加速。

静态流体中任何点的压力仅取决于该点的深度。如前所述，由于流体的重量超过特定水平，地球附近流体中的压力随深度而变化。在上面的示例中，我们假设密度是恒定的，并且流体的平均密度可以很好地表示密度。对于像水这样的液体，这是一个合理的近似值，在这些液体中，压缩液体或改变体积需要很大的力。例如，在游泳池中，密度几乎是恒定的，底部的水几乎不会被顶部水的重量压缩。但是，在大气层中向上旅行的情况却完全不同。在距离地球表面不远的地方，空气的密度开始发生显著变化。

要得出地球表面含有密$\rho$度流体的储罐中压力随深度变化的公式，我们必须从流体的密度不恒定的假设开始。由于位于其上方的流体的重量，位于更深层的流体比靠近表面的流体承受的力更大。因此，在给定深度计算的压力与使用恒定密度计算的压力不同。

想象一下深度为 h 的薄流体元素，如图所示$\PageIndex{3}$。假设元素的横截面面积为 A 和高度$\Delta$ y。作用在元素上的力是由上方 p (y) 和其下方 p (y +$\Delta$ y) 的压力。元素本身的重量也显示在自由体图中。

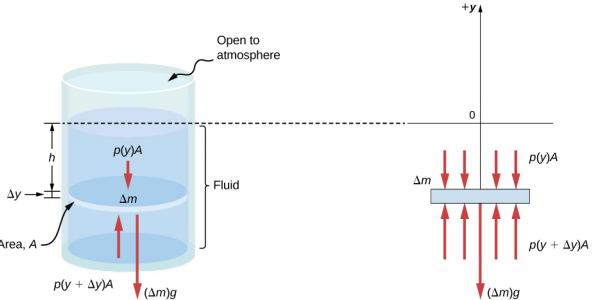
图 A 是一个装满流体且顶部通向大气的圆柱体的示意图。在流体中放置质量为 Delta m 的圆盘，表面积 A 与圆柱体的表面积相同，高度为 Delta y。高度为 h 的流体位于圆盘上方。图 B 是圆盘表示的力 Delta m x g、圆盘上方流体施加的 p (y) x A 以及圆盘下方流体施加的 p (y + Delta y) x A 的示意图。 — 图$\PageIndex{3}$：流体内部质量元素上的力。元素本身的重量显示在自由体图中。

由于 y 和 y +$\Delta$ y 之间的流体元素没有加速，因此力是平衡的。使用朝上的笛卡尔y轴，我们找到了y分量的以下方程：

\[p(y + \Delta y)A - p(y)A - g \Delta m = 0(\Delta y < 0) \ldotp \label{14.6}\]

请注意，如果元素的加速度分量为非零，则右侧不会为零，而是质量乘以 y 加速度。元素的质量可以用流体的密度和元素的体积来书写：

\[\Delta m = |\rho A \Delta y| = - \rho A \Delta y \quad (\Delta y < 0) \ldotp\]

将$\Delta$ m 的这个表达式放入方程\ ref {14.6} 然后将两边除以 A$\Delta$ y，我们发现

\[\frac{p(y + \Delta y) - p(y)}{\Delta y} = - \rho g \ldotp \label{14.7}\]

取无穷薄元素$\Delta$ y → 0 的极限，我们得出以下微分方程，该方程给出了流体中压力的变化：

\[\frac{dp}{dy} = - \rho g \ldotp \label{14.8}\]

这个方程告诉我们，流体中压力的变化速率与流体的密度成正比。该方程的解取决于密度$\rho$是恒定还是随深度而变化；即函数$\rho$ (y)。

如果所分析的深度范围不太大，我们可以假设密度是恒定的。但是，如果深度范围足够大，密度可以明显变化，例如大气层，则密度会随着深度的变化而发生显著变化。在这种情况下，我们不能使用恒定密度的近似值。

密度恒定流体中的压力

让我们使用方程式\ ref {14.9} 来计算出一个在水等液体罐中距离表面 h 深度处的压力的公式，其中液体的密度可以说是恒定的。

将装满液体的烧杯示意图显示为高度 h。流体在表面显示压力 P0 等于零，在烧杯底部显示压力 P。

我们需要将方程\ ref {14.9} 从 y = 0（其中压力为大气压力 (p _0)）到 y = −h（深度的 y 坐标）进行积分：

\[\begin{split} \int_{p_{0}}^{p} dp & = - \int_{0}^{-h} \rho gdy \\ p - p_{0} & = \rho gh \\ p & = p_{0} + \rho gh \ldotp \end{split} \label{14.9}\]

因此，正如我们之前发现的那样，如果流体的密度在$\rho$高处恒定，则地球表面流体深度的压力等于大气压加上gh。

请注意，流体中的压力仅取决于距表面的深度，而不取决于容器的形状。因此，在流体可以在各个部分自由移动的容器中，无论形状如何，液体在每个部分都保持相同的水平，如图所示$\PageIndex{4}$。

几个不同形状的玻璃容器的照片，这些容器由底部的玻璃管连接起来，里面装满了红色液体。液体在不同的玻璃容器中处于相同的高度。 — 图$\PageIndex{4}$：如果流体可以在容器的各个部分之间自由流动，则它在每个部分上升到相同的高度。在图中的容器中，每列底部的压力是相同的；如果不相同，流体将流动，直到压力变为相等。

大气压随高度的变化

大气压随高度的变化特别令人感兴趣。假设空气的温度是恒定的，并且理想的热力学气体定律很好地描述了大气的近似值，那么当温度恒定时，我们可以找到大气压随高度的变化。（我们将在后面的章节中讨论理想的气体定律，但我们假设你在高中和化学阶段就已经熟悉了。）假设 p (y) 是高度 y 处的大气压力。y$\rho$ 处的密度、开尔文标度 (K) 中的温度 T 和空气分子的质量 m 与理想气体定律下的绝对压力有关，形式为

\[p = \rho \frac{k_{B} T}{m}\; (atmosphere), \label{14.10}\]

其中 k _B 是玻尔兹曼常数，其值为 1.38 x 10 ⁻²³ J/K。

你可能遇到了理想的气体定律，形式为 pV = nRT，其中 n 是摩尔数，R 是气体常数。在这里，同样的定律是用不同的形式写成的，使用密度$\rho$而不是体积 V。因此，如果压力 p 随高度而变化，密度也会随之变化$\rho$。使用理想气体定律得出的密度，压力随高度的变化率计算为

\[\frac{dp}{dy} = -p \left(\dfrac{mg}{k_{B} T}\right),\]

其中，括号内收集了恒定量。用单个符号替换这些常量$\alpha$，方程看起来要简单得多：

\[\begin{split} \frac{dp}{dy} & = - \alpha p \\ \frac{dp}{p} & = - \alpha dy \\ \int_{p_{0}}^{p(y)} \frac{dp}{p} & = \int_{0}^{y} - \alpha dy \\ [\ln (p)]_{p_{0}}^{p(y)} & = [- \alpha y]_{0}^{y} \\ \ln (p) - \ln (p_{0}) & = - \alpha y \\ \ln \left(\dfrac{p}{p_{0}}\right) & = - \alpha y \end{split}\]

这给出了解决方案

\[p(y) = p_{0} e^{- \alpha y} \ldotp\]

因此，大气压随高度呈指数级下降，因为 y 轴从地面指向上方，而 y 在海平面以上的大气层中具有正值。压力下降了高度为$\frac{1}{e}$何时为一个系数$\frac{1}{\alpha}$，这为我们提供了物理解释$\alpha$：常数$\frac{1}{\alpha}$是一个长度刻度，用于描述压力如何随身高变化，通常被称为压力标高度。

$\alpha$通过使用氮分子的质量作为空气分子的代理，我们可以获得近似值。我们发现，在 27 °C 或 300 K 的温度下

\[\alpha = - \frac{mg}{k_{B} T} = \frac{(4.8 \times 10^{-26}\; kg) \times (9.81\; m/s^{2})}{(1.38 \times 10^{-23}\; J/K) \times (300\; K)} = \frac{1}{8800\; m} \ldotp\]

因此，每 8800 米，气压就会下降一倍，约为其值的三分之一。这只能使我们对实际情况有一个粗略的估计，因为我们假设在离地球这么远的距离内既是恒定温度又是恒定的 g，这两者在现实中都不正确。

流体中的压力方向

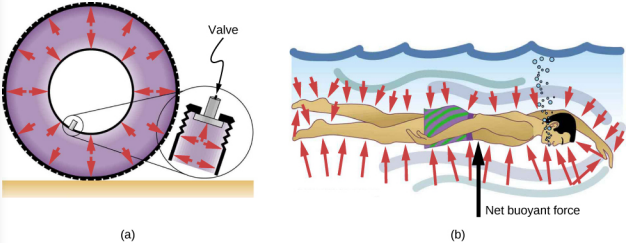
流体压力没有方向，是标量，而压力产生的力有明确的方向：它们总是垂直于任何表面施加。原因是流体无法承受或施加剪切力。因此，在封闭在储罐中的静态流体中，施加在储罐壁上的力垂直于内表面施加。同样，压力是垂直于流体中任何物体的表面施加的。该图$\PageIndex{5}$说明了空气对轮胎壁施加的压力，以及水对游泳运动员身体施加的压力。

图 A 是充满空气的轮胎的示意图。轮胎内部的压力施加的力垂直于其接触的所有表面，包括气门。图 B 是水下游泳运动员的示意图。压力垂直于该游泳运动员的四面施加，在游泳运动员的下方施加的净浮力更大。 — 图$\PageIndex{5}$：(a) 轮胎内部的压力施加垂直于其接触的所有表面的力。箭头表示在不同点施加的力的方向和大小。 (b) 压力垂直于该游泳运动员的所有侧面施加，因为如果他不在场，水会流入他所占据的空间。箭头表示在游泳运动员身上不同位置施加的力的方向和大小。请注意，下方的力更大，因为深度更大，会产生向上的净力或浮力。游泳运动员的净垂直力等于浮力与游泳运动员重量的总和。