14.2：流体、密度和压力（第 1 部分）

Last updated
Save as PDF

Page ID: 205068

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

陈述物质的不同阶段
在分子或原子层面上描述物质相的特征
区分可压缩材料和不可压缩材料
定义密度及其相关的 SI 单位
比较和对比各种物质的密度
定义压力及其相关的 SI 单位
解释压力和力之间的关系
计算给定压力和面积的力

物质通常以固体、液体或气体的形式存在；这些状态被称为物质的三个常见相。在本节中，我们将详细介绍每个阶段。

固体的特性

固体是刚性的，具有特定的形状和一定的体积。固体中的原子或分子彼此非常接近，并且这些分子之间有很大的力。固体的形式将由分子之间这些力的性质决定。尽管真正的固体不是不可压缩的，但它需要很大的力才能改变固体的形状。在某些情况下，分子之间的力会导致分子组织成晶格，如图所示\(\PageIndex{1}\)。这种三维晶格的结构表现为由刚性键连接的分子（建模为硬弹簧），这允许有限的运动自由度。即使是很大的力也只能在晶格的原子或分子中产生很小的位移，并且固体保持其形状。固体还能抵抗剪切力。（剪切力是切向施加到表面的力，如静态平衡和弹性中所述。）

流体的特性

液体和气体被认为是流体，因为它们会产生剪切力，而固体会抵抗它们。像固体一样，液体中的分子与相邻的分子结合，但这些键的数量要少得多。液体中的分子没有锁定在原位，可以相对于彼此移动。分子之间的距离类似于固体中的距离，因此液体具有一定的体积，但是液体的形状会根据其容器的形状而变化。气体不会与相邻的原子结合，分子之间可以有很大的分离。气体既没有特定的形状也没有确定的体积，因为它们的分子会移动以填充它们所在的容器（图\(\PageIndex{1}\)）。

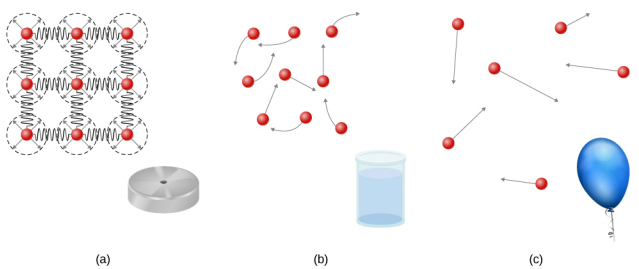
图 A 显示了固体中原子的排列。原子与相邻的原子密切接触，并由弹簧表示的力保持在原位。图B显示了液体中原子的排列。原子也密切接触，但可以相互滑动。图C显示了气体中原子的排列。原子自由移动，相隔很远。 — 图\(\PageIndex{1}\)：(a) 固体中的原子总是与相邻的原子密切接触，由此处以弹簧表示的力保持在原位。 (b) 液体中的原子也密切接触，但可以相互滑动。原子之间的力强烈抵抗压缩原子的尝试。 (c) 气体中的原子自由移动并相隔很远的距离。气体必须存放在密闭的容器中，以防止其自由膨胀和逸出。

液体在受力时很容易变形，一旦力消失，也不会恢复到原来的形状。之所以发生这种情况，是因为液体中的原子或分子可以自由滑动并改变邻域。也就是说，液体流动（所以它们是一种流体），分子通过相互吸引而结合在一起。当将液体放入没有盖子的容器中时，它会留在容器中。由于原子密集在一起，液体（如固体）会抵抗压缩；改变液体的体积需要极大的力。

相比之下，气体中的原子相隔很远，因此气体中原子之间的力非常弱，除非原子相互碰撞。这使得气体相对容易压缩并允许它们流动（这使它们成为流体）。与液体不同，当放入敞开的容器中时，气体会逸出。

在本章中，我们通常将气体和液体都简单地称为流体，只有在它们的行为不同时才区分它们。还有另一种物质相，即等离子体，它存在于非常高的温度下。在高温下，分子可能会分解成原子，原子分解成电子（带负电荷）和质子（带正电荷），形成等离子体。本章将不深入讨论等离子体，因为由于电荷之间的强电力，等离子体的特性与本章讨论的其他三个常见物质相截然不同。

密度

假设一块黄铜和一块木头的质量完全相同。如果两个方块都掉在水箱里，为什么木头会漂浮而黄铜会下沉（图\(\PageIndex{2}\)）？之所以发生这种情况，是因为黄铜的密度比水大，而木材的密度比水低。

图 A 是一张位于刻度上的一大块木头和一小块黄铜的照片。刻度表示两个方块的重量相同。图 B 是一张装满水的鱼缸里一大块木头的照片。小黄铜块沉到底部，而木块漂浮。 — 图\(\PageIndex{2}\)：（a）一块黄铜和一块木块的重量和质量相同，但是木块的体积要大得多。 (b) 当放在装满水的鱼缸中时，黄铜水槽和木块会漂浮起来。（两张照片中的木块都是一样的；为了适应体重秤，它被侧面翻过来了。）

密度是物质的重要特征。例如，它在确定物体是否沉入或漂浮在流体中至关重要。

密度

物质或物体的平均密度定义为其单位体积的质量,

\[\rho = \frac{m}{V} \label{14.1}\]

其中希腊字母\(\rho\) (rho) 是密度的符号，m 是质量，V 是体积。

密度单位为 kg/m ³。表 14.1 列出了一些代表性值。 cgs 的密度单位是克每立方厘米 g/cm ³，其中

\[1\; g/cm^{3} = 1000\; kg/m^{3} \ldotp\]

公制系统最初的设计目的是使水的密度为 1 g/cm ³，相当于 103 kg/m ³。因此，基本质量单位千克最初被设计为1000 mL水的质量，其体积为1000 cm ³。

表 14.1-一些常见物质的密度

固体	(0.0 °C)	液体	(0.0 °C)	气体	(0.0 °C ,101.3 kPa)
物质	\(\rho\)（kg/m ³）	物质	\(\rho\)（kg/m ³）	物质	\(\rho\)（kg/m ³）
铝	2.70 x 10 ³	苯	8.79 x 10 ²	空气	1.29 x 10 ⁰
骨头	1.90 x 10 ³	血	1.05 x 10 ³	二氧化碳	.1.98 x 10 ⁰
黄铜	8.44 x 10 ³	乙醇	8.06 x 10 ²	一氧化碳	1.25 x 10 ⁰
混凝土	2.40 x 10 ³	汽油	6.80 x 10 ²	氦气	1.80 x 10 ^-1
铜	8.92 x 10 ³	甘油	1.26 x 10 ³	氢气	9.00 x 10 ^-2
软木	2.40 x 10 ²	水星	1.36 x 10 ⁴	甲烷	7.20 x 10 ^-2
地壳	3.30 x 10 ³	橄榄油	9.20 x 10 ²	氮气	1.25 x 10 ⁰
玻璃	2.60 x 10 ³			一氧化二氮	1.98 x 10 ⁰
花岗岩	2.70 x 10 ³			氧气	1.43 x 10 ⁰
铁	7.86 x 10 ³
领导	1.13 x 10 ⁴
橡树	7.10 x 10 ²
松树	3.73 x 10 ²
铂	2.14 x 10 ⁴
聚苯乙烯	1.00 x 10 ²
钨	1.93 x 10 ⁴
铀	1.87 x 10 ³

通过查看表 14.1 可以看出，物体的密度可能有助于识别其构成。例如，金的密度约为铁密度的2.5倍，约为铝密度的2.5倍。密度还揭示了物质的相位及其子结构。请注意，液体和固体的密度大致相当，这与它们的原子密切接触的事实一致。气体的密度远低于液体和固体的密度，因为气体中的原子被大量的空白空间隔开。显示气体的标准温度为 0.0 °C，标准压力为 101.3 kPa，密度与温度和压力有很强的依赖性。显示的固体和液体的密度是在 0.0 °C 的标准温度下给出的，固体和液体的密度取决于温度。固体和液体的密度通常会随着温度的降低而增加。

表 14.2 显示了不同阶段和温度下的水密度。水的密度随着温度的降低而增加，在4.0°C时达到最大值，然后随着温度降至4.0°C以下而降低。水密度的这种行为解释了为什么冰在水体顶部形成。

表 14.2-水的密度

物质	\(\rho\)（kg/m ³）
冰 (0 °C)	\ (\ rho\) (kg/m3)” style= “text-align: center;” class= “lt-phys-4055” >9.17 x 10 ²
水 (0 摄氏度)	\ (\ rho\) (kg/m3)” style= “text-align: center;” class= “lt-phys-4055” >9.998 x 10 ²
水 (4 摄氏度)	\ (\ rho\) (kg/m3)” style= “text-align: center;” class= “lt-phys-4055” >1.000 x 10 ³
水 (20 摄氏度)	\ (\ rho\) (kg/m3)” style= “text-align: center;” class= “lt-phys-4055” >9.982 x 10 ²
水 (100 °C)	\ (\ rho\) (kg/m3)” style= “text-align: center;” class= “lt-phys-4055” >9.584 x 10 ²
蒸汽（100 °C，101.3 kPa）	\ (\ rho\) (kg/m3)” style= “text-align: center;” class= “lt-phys-4055” >1.670 x 10 ²
海水 (0°C)	\ (\ rho\) (kg/m3)” style= “text-align: center;” class= “lt-phys-4055” >1.030 x 10 ³

在物质的整个体积中，物质的密度不一定是恒定的。如果整个物质的密度恒定，则该物质被认为是均质物质。固体铁棒是均质物质的一个例子。整个密度是恒定的，该物质的任何样品的密度与其平均密度相同。如果物质的密度不恒定，则该物质被称为异质物质。一块瑞士奶酪就是一种含有固体奶酪和充气孔隙的异质材料的例子。异质材料中特定位置的密度称为局部密度，以位置的函数形式给出，\(\rho\)=\(\rho\) (x, y, z)（图\(\PageIndex{3}\)）。

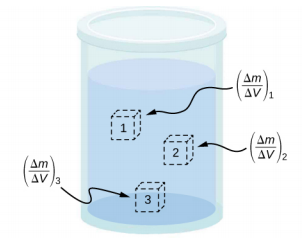
图是一张装满液体的容器的图。在容器的不同区域绘制小立方体以表示局部密度点。 — 图\(\PageIndex{3}\)：在整个异质混合物中，密度可能会有所不同。某一点的局部密度是通过在给定点周围的小体积中将质量除以体积获得的。

局部密度可以通过限制过程获得，该过程基于相关点周围小体积的平均密度，取体积大小接近零的极限，

\[\rho = \lim_{\Delta V \rightarrow 0} \frac{\Delta m}{\Delta V} \label{14.2}\]

其中\(\rho\)是密度，m 是质量，V 是体积。

由于气体可以自由膨胀和收缩，因此气体的密度随温度变化很大，而液体的密度随温度的变化很小。因此，液体的密度通常被视为恒定密度，密度等于平均密度。

密度是一种尺寸特性；因此，在比较两种物质的密度时，必须考虑单位。出于这个原因，通常使用一种称为比重的更方便、无量纲的量来比较密度。比重定义为材料的密度与水的密度之比，在 4.0 °C 和一个压力大气中，即 1000 kg/m ³：

\[Specific\; gravity = \frac{Density\; of\; material}{Density\; of\; water} \ldotp\]

比较使用水，因为水的密度为 1 g/cm ³，最初用于定义千克。比重是无量纲的，可以在材料之间进行即时比较，而不必担心密度单位。例如，铝的密度在 g/cm ³ 中为 2.7（以 kg/m ³ 为单位，2700），但无论密度单位如何，其比重均为 2.7。就浮力而言，比重是一个特别有用的量，我们将在本章后面讨论这个问题。

压力

毫无疑问，你听说过 “压力” 一词用于血液（高血压或低血压）和天气（高压和低压天气系统）。这只是流体中压力的众多例子中的两个。（回想一下，我们在体积应力和应变的背景下在静态平衡和弹性中引入了压力的概念。）

压力

压力 (p) 定义为施加力的单位面积 A 的法向力 F，或

\[p = \frac{F}{A} \ldotp \label{14.3}\]

为了定义特定点的压力，压力被定义为流体在包含该点的面积 dA 的无穷小元素上施加的力 dF，得到 p =\(\frac{dF}{dA}\)。

给定的力可能产生明显不同的效果，具体取决于施加力的区域。例如，施加于 1 mm ² 区域的力所产生的压力是施加于 1 cm ² 区域的相同力的 100 倍。这就是为什么当施加微小的力时，锋利的针头能够刺穿皮肤，但是用手指施加同样的力不会刺穿皮肤（图\(\PageIndex{4}\)）。

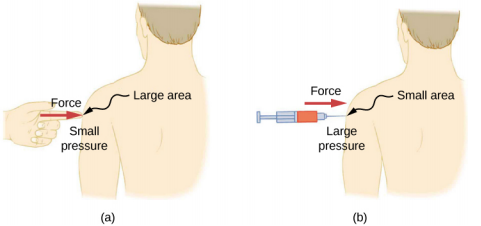
图 A 是一幅用手指戳住肩膀的人的画。显示手指的力量占据了更大的区域，这只会产生少量的压力。图 B 是一幅有人被肩上有针头的注射器戳的画作。如图所示，注射器的力量占用的面积较小，从而产生很大的压力。 — 图\(\PageIndex{4}\)：(a) 被手指戳的人可能会受到刺激，但用力几乎没有持久的效果。 (b) 相比之下，对像针尖端一样大小的区域施加同样的力足以折断皮肤。

请注意，尽管力是矢量，但压力是标量。压力是一个标量，因为它被定义为与垂直于表面积的力的大小成正比。压力的 SI 单位是帕斯卡（Pa），以法国数学家和物理学家布莱斯·帕斯卡（1623—1662 年）的名字命名，其中

\[1\; Pa = 1\; N/m^{2} \ldotp\]

其他几个单位用于表示压力，我们将在本章后面讨论这些单位。