Skip to main content
Global

13.E: 引力（练习）

  1. Last updated
  2. Save as PDF
  • Page ID
    204492

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    概念性问题

    13.1 牛顿万有引力定律

    1. 远距离行动，例如重力，曾经被认为是不合逻辑的，因此是不真实的。 科学中真理的最终决定因素是什么？为什么这种远距离行动最终被接受？
    2. 在万有引力定律中，牛顿假设力与两个质量的乘积成正比（~m 1 m 2）。 尽管所有科学猜想都必须经过实验验证，但你能否提供论据说明为什么必须如此？ （你不妨考虑一些简单的例子，在这些例子中，任何其他形式都会导致相互矛盾的结果。）

    13.2 地球表面附近的引力

    1. 工程师在赤道以外的任何地方或非常靠近两极的地方建造非常高的建筑物时，是否必须考虑地球的自转？

    13.3 引力势能和总能量

    1. 据称，总能量为负的卫星处于限定轨道上，而总能量为零或正的卫星处于无界轨道上。 为什么这是真的？ 在引力势能方面做出了什么选择才是真的？
    2. 研究表明，将卫星送入低地球轨道所需的能量（势能的变化）只是保持其在轨道上所需动能的一小部分。 对于较大的轨道来说是这样吗？ 随着轨道大小的增加，动能与势能的变化之比是否有趋势？

    13.4 卫星轨道和能量

    1. 一位学生认为，轨道上的卫星处于自由落体状态，因为卫星不断向地球坠落。 另一个人说，轨道上的卫星不是自由落体的，因为重力引起的加速度不是9.80 m/s 2。 你同意谁的看法，为什么？
    2. 许多卫星被放置在地球同步轨道上。 这些轨道有什么特别之处？ 对于一个全球通信网络，需要多少颗这样的卫星？

    13.5 开普勒的行星运动定律

    1. 开普勒定律纯粹是描述性的，还是包含因果信息？
    2. 在下图中，对于质量要大得多的椭圆轨道上的卫星，请指明其速度最快的位置，哪里最小。 什么保护法规定了这种行为？ 指明这些点的力、加速度和速度的方向。 在 y 轴相交的两个点（沿半短轴）为这三个相同的量绘制矢量，由此确定速度是在增加、减小还是处于最大/最小值。

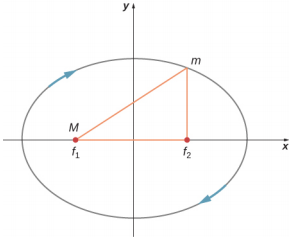
    显示 x y 坐标系和椭圆的示意图，以原点为中心，焦点在 x 轴上。 左边的焦点标记为 f 1 和 M。右边的焦点标记为 f 2。 标记为 m 的位置如上方的 f 2 所示。 由 f 1、f 2 和 m 定义的直角三角形以红色显示。 与椭圆相切的顺时针方向由蓝色箭头指示。

    13.6 潮汐力量

    1. 当物体落入黑洞时，潮汐力会增加。 当物体接近施瓦茨柴尔德半径时，这些潮汐力量是否总是会将其撕裂？ 黑洞的质量和物体的大小如何影响你的答案？

    13.7 爱因斯坦的引力理论

    1. 等效原理指出，实验室在均匀引力场中进行的所有实验都无法与不在引力场中但正在均匀加速的实验室中进行的实验区分开来。 对于后一种情况，请考虑一下在某个高度完美地水平射向地面、穿过加速实验室的激光束会发生什么情况。 （从实验室外的非加速帧中观看。） 相对于激光的高度，激光束在哪里会撞到远处的墙壁？ 这说明了引力场对光的影响？ 光没有质量的事实对这个论点有什么区别吗？
    2. 当一个人接近黑洞的施瓦茨柴尔德半径时，外部观察者会看到该人的所有过程（他们的时钟、心率等）减速，并在他们到达施瓦茨柴尔德半径时停止。 （掉入黑洞的人看到自己的过程不受影响。） 但是所有观察者的光速在任何地方都是一样的。 当你接近黑洞时，这对太空有什么影响？

    问题

    13.1 牛顿万有引力定律

    1. 评估两个 5 kg 球形钢球之间的重力大小，中间距离为 15 cm。
    2. 估计两个相扑选手（质量为 220 kg 和 240 kg）在被拥抱且中心相距 1.2 米时之间的引力。
    3. 占星术占据了行星出生时的大部分位置。 行星对地球施加的唯一已知力是引力。 (a) 计算一个在0.200米外出生的100公斤的父亲对一个4.20公斤的婴儿施加的引力（他在帮忙，所以他离孩子很近）。 (b) 计算如果木星距离地球最近，距离大约 6.29 x 10 11 米，则对宝宝施加的力。 木星对宝宝的力量与父亲对宝宝的力量相比如何？ 房间和医院大楼中的其他物体也会施加类似的引力。 （当然，可能有未知的力量在起作用，但科学家们首先需要确信甚至会产生影响，更不用说未知力量造成影响了。）
    4. 距离人10.0公里的山对他施加的引力等于他体重的2.00％。 (a) 计算山的质量。 (b) 将山的质量与地球的质量进行比较。 (c) 这些结果有什么不合理之处？ (d) 哪些前提不合理或不一致？ （请注意，精确的引力测量可以轻松检测到附近山脉的影响和当地地质变化的影响。）
    5. 国际空间站的质量约为37万千克。 (a) 如果 150 公斤的合身宇航员距离空间站质心 20 米，她的力量是多少？ (b) 你认为你的答案有多准确？
    显示了国际空间站的图像。
    图 13.33（来源：©ESA—David Ducros）
    1. 2006 年，小行星 Toutatis 在地球附近飞行，距离月球的距离是我们月球的四倍。 这是我们在2060年之前最接近的方法。 如果它的质量为 5.0 x 10 13 kg，那么它在最接近地球时对地球施加了什么力？
    2. (a) 小行星图塔蒂斯（见上一个问题）在最接近时造成的地球加速是多少？ (b) 此时 Toutatis 的加速速度是多少？

    13.2 地球表面附近的引力

    1. (a) 计算地球的质量，因为测得的北极重力引起的加速度为9.832 m/s 2，极点处的地球半径为6356 km。 (b) 将其与美国宇航局的地球概况介绍值5.9726 x 10 24 kg进行比较。
    2. (a) 月球表面重力引起的加速度是多少？ (b) 在火星表面？ 火星的质量为 6.418 x 10 23 千克，其半径为 3.38 x 10 6 m。
    3. (a) 计算由太阳表面重力引起的加速度。 (b) 如果你能站在太阳上，你的体重会增加什么因素？ （没关系，你不能。）
    4. 颗粒的质量为 15 千克。 (a) 它在地球上的重量是多少？ (b) 它在月球上的重量是多少？ (c) 它在月球上的质量是多少？ (d) 它在远离任何天体的外层空间中的重量是多少？ (e) 此时的质量是多少？
    5. 在半径为 1.2 x 10 7 m 的行星上，重力引起的加速度为 18 m/s 2。 这个星球的质量是多少？
    6. 土星的平均直径为 1.2 x 10 8 m，其平均质量密度为 0.69 g/cm 3。 找出土星表面的重力引起的加速度。
    7. 水星的平均直径为4.88 x 10 6 m，其表面重力引起的加速度为3.78 m/s 2。 估计这颗行星的质量。
    8. 由行星表面引力引起的加速度是其在地球表面的三倍。 众所周知，这颗行星的质量密度是地球的两倍。 就地球的半径而言，这颗行星的半径是多少？
    9. 行星表面与地球半径相同的天体重量是其在地球上的重量的 10 倍。 就地球的质量而言，这颗行星的质量是多少？

    13.3 引力势能和总能量

    1. 找出弹丸从火星表面的逃生速度。
    2. 找出弹丸从木星表面逃脱的速度。
    3. 位于月球绕地球轨道的卫星的逃生速度是多少？ 假设月亮不在附近。
    4. (a) 评估两个 5.00 千克的球形钢球之间的引力势能，中间距离为 15.0 cm。 (b) 假设它们最初在深空相对于彼此处于静止状态，则使用节能来确定它们在撞击时能以多快的速度移动。 每个球体的半径为 5.10 厘米。
    5. 探测到一颗距离地球 5.0 x 10 7 千米的中等大小的小行星以 2.0 km/s 的速度直接驶向地球。在撞击我们的大气层之前，它的速度会是多少？ （你可以忽略小行星的大小。）
    6. (a) 在上一个问题中，小行星在撞击地球之前的动能将是多少？ b) 将这种能量与最大的裂变炸弹 2100 TJ 的输出进行比较。 这会对地球产生什么影响？
    7. (a) 从地球表面的静止状态中取出并置于月球表面的1000千克有效载荷的能量变化如何？ (b) 如果有效载荷从月球表面带到地球，答案会是什么？ 这是对来回移动有效载荷所需的能量的合理计算吗？

    13.4 卫星轨道和能量

    1. 如果一颗质量是地球1.5倍的行星在地球轨道上行驶，它的周期会是多少？
    2. 围绕恒星绕圆轨道的两颗行星的速度为 v 和 2v。 (a) 行星轨道半径的比率是多少？ (b) 他们的周期比率是多少？
    3. 使用地球与太阳的平均距离和地球的轨道周期，（a）找出地球绕太阳运动的向心加速度。 (b) 将该值与地球自转导致的赤道向心加速度值进行比较。
    4. 周期为 1.00 h 的地球卫星的轨道半径是多少？ (b) 这个结果有什么不合理之处？
    5. 根据地球轨道数据计算太阳的质量，并将获得的值与太阳的实际质量进行比较。
    6. 根据木星最内层的月球艾奥的平均轨道半径为421,700 km，周期为1.77天这一事实来找出木星的质量。
    7. 对银河系的天文观测表明，它的质量约为8.0 x 10 11 个太阳质量。 在银河系外围运行的恒星距离其中心约 6.0 x 10 4 光年。 (a) 该恒星的轨道周期应该是多少？ (b) 相反，如果它的周期是 6.0 x 10 7 年，那么银河系的质量是多少？ 这样的计算被用来暗示其他物质的存在，例如银河系中心有一个非常大的黑洞。
    8. (a) 为了防止小型卫星漂移到附近的小行星上，将其置于周期为3.02小时、半径为2.0千米的轨道上。 小行星的质量是多少？ (b) 就轨道的大小而言，这个质量似乎合理吗？
    9. 月球和地球围绕其共同的质心旋转，该质心距离地球中心约4700公里。 （这是地表以下 1690 千米处。） (a) 计算该点由于月球的重力而产生的加速度。 (b) 计算地球中心每个农历月绕该点旋转一次时的向心加速度（大约 27.3 d），并将其与（a）部分中发现的加速度进行比较。 评论它们是否平等以及为什么应该或不应该平等。
    10. 太阳每隔 2.60 x 10 8 年绕银河系运行一次，轨道大致为圆形，平均半径为 3.00 x 10 4 光年。 （光年是指光在 1 年内行驶的距离。） 计算太阳在其银河轨道上的向心加速度。 你的结果是否支持这样的论点，即在太阳上可以找到一个近乎惯性的参考框架？ (b) 计算太阳在其银河轨道上的平均速度。 答案让你感到惊讶吗？
    11. 地球同步地球卫星是轨道周期恰好为一天的卫星。 这种轨道可用于通信和天气观测，因为卫星保持在地球上的同一点上方（前提是它在赤道平面上以与地球自转的方向相同的方向运行）。 根据附录D 中的地球数据计算此类轨道的半径。

    13.5 开普勒的行星运动定律

    1. 根据平均地球轨道数据计算太阳的质量，并将获得的值与太阳通常列出的值1.989 x 10 30 kg进行比较。
    2. 艾奥绕木星运行，平均半径为421,700千米，周期为1.769天。 根据这些数据，木星的质量是多少？
    3. 列出的绕太阳运行的天文物体的 “平均” 轨道半径通常不是综合平均值，而是计算得出正确的周期，将其应用于圆形轨道方程时。 有鉴于此，就远日点和近日点而言，平均轨道半径是多少？
    4. 哈雷彗星的近日点为 0.586 AU，远日点为 17.8 AU。 鉴于它在近日点的速度为 55 km/s，那么远日点（1 AU = 1.496 x 10 11 m）的速度是多少？ （提示：你可以使用能量守恒或角动量，但后者要容易得多。）
    5. Lagerkvist 彗星的近日点为 2.61 AU，周期为 7.36 年。 证明这颗彗星的远日点为 4.95 AU。
    6. 在前一个问题中，拉格克维斯特彗星的近日点速度与远日点速度的比率是多少？
    7. 爱神有一个绕太阳的椭圆轨道，近日点距离为1.13 AU，远日点距离为1.78 AU。 它的轨道周期是多少？

    13.6 潮汐力量

    1. (a) 由于木星，艾奥近侧和远侧1.0千克质量上的力有什么区别？ 艾奥的平均半径为1821千米，木星周围的平均轨道半径为421,700千米。 (b) 将此差异与示例 13.14 中计算的地球与月球之间的差异计算得出的差异进行比较。 潮汐力量是艾奥火山活动的原因。
    2. 如果太阳坠入黑洞，调查员的不可逆转点将距离中心奇点大约 3 公里。 即使在离中心300公里的地方，调查员还能活下来吗？ 答案是找出黑洞对调查者头部和脚部1.0千克质量施加的引力吸引力的差异。
    3. 以《潮汐力量》中的图 13.23 为例。 此图表示春季潮汐的潮汐力。 绘制类似的潮汐图。 （提示：为简单起见，想象一下太阳和月亮的贡献是相同的。 你的图将是两个力场的向量和（如图 13.23 所示），减去二倍，然后以直角叠加。）

    13.7 爱因斯坦的引力理论

    1. 如果我们银河系中心的黑洞的质量为400万个太阳质量，那么施瓦茨柴尔德的半径是多少？
    2. 如果我们由1000亿颗恒星组成的银河系崩溃成黑洞，在光年内，施瓦茨柴尔德的半径会是多少？ 相比之下，我们与中心的距离约为13,000光年。

    其他问题

    1. 中子星是一颗具有核密度的寒冷、崩溃的恒星。 一颗特定的中子星的质量是我们太阳的两倍，半径为12.0 km。 (a) 一个100公斤的宇航员站在其表面上的重量是多少？ (b) 这告诉我们关于降落在中子星上的什么？
    2. (a) 地球和月球在物体上的净引力离地球中心多远会为零？ (b) 将力的大小设置为相等应该从二次曲线中得出两个答案。 你明白为什么有两个位置，但净力为零的位置只有一个位置吗？
    3. 距离太阳中心多远，太空飞船上地球和太阳的净引力会为零？
    4. 根据地球特性的以下变化，计算地球表面 g 的值：（a）其质量增加一倍，半径减半；（b）其质量密度增加一倍，半径不变；（c）其质量密度减半，质量保持不变。
    5. 假设你可以与另一个太阳系中行星的居民进行通信。 他们告诉你，在他们的星球上，直径和质量分别为5.0 x 10 3 km和3.6 x 10 23 kg，跳高记录是2.0 m。鉴于这个记录在地球上接近 2.4 米，你会对你的外星朋友的跳跃能力得出什么结论？
    6. (a) 假设您在赤道测量的重量是您在质量和直径等于地球质量和直径的行星上测得的重量的一半。 行星的旋转周期是多少？ (b) 你需要考虑这个星球的形状吗？
    7. 重量为 100 kg 的物体在北极和赤道用弹簧秤称重。 这两个点的刻度读数是多少？ 假设极点处 g = 9.83 m/s 2。
    8. 找到从地球表面逃离太阳系所需的速度。 假设没有其他天体参与，也不考虑地球在其轨道上运动的事实。 [提示：方程式 13.6 不适用。 使用方程式 13.5 并包括地球和太阳的势能。
    9. 考虑前面的问题，包括地球绕太阳的轨道速度为29.8 km/s这一事实。（a）相对于地球需要多大的速度以及你应该朝哪个方向离开地球？ (b) 轨道的形状将如何？
    10. 从太阳 1.50 AU 观测到一颗彗星，速度为 24.3 km/s。这颗彗星是在限定轨道还是未绑定轨道上？
    11. 当小行星距离太阳 2.00 AU 时，它的速度为 15.5 km/s。 最接近时，它距离太阳 0.400 AU。 那时的速度是多少？
    12. 旧卫星及其发射器留下的空间碎片正在成为其他卫星的危险。 (a) 计算卫星在距离地球表面900千米的轨道上的速度。 (b) 假设在半径相同的轨道上有一个松散的铆钉，该轨道以90°的角度与卫星的轨道相交。 在撞击卫星之前，铆钉相对于卫星的速度是多少？ (c) 如果其质量为0.500 g，并且停留在卫星内，则碰撞会产生多少以焦耳为单位的能量？ （假设卫星的速度变化不大，因为它的质量远大于铆钉的质量。）
    13. 一颗质量为1000 kg的卫星在环绕地球的轨道上。 卫星轨道的半径等于地球半径的两倍。 (a) 卫星有多远？ (b) 找出卫星的动能、势能和总能量。
    14. 谷神星被提升为矮行星后，我们现在认出已知最大的小行星是维斯塔，其质量为2.67 x 10 20 kg，直径从578公里到458千米不等。 假设 Vesta 是半径为 520 km 的球形，则求出从其表面逃逸的近似速度。
    15. (a) 使用前一问题中有关小行星维斯塔的数据，空间探测器在距离其表面10.0公里的圆轨道上的轨道周期是多少？ (b) 为什么这种计算充其量是微不足道的？
    16. 我们的太阳系围绕银河系中心的轨道速度是多少？ 假设半径球体内的质量等于我们离中心的距离，大约是 1000 亿个太阳质量。 我们与中心的距离是 27,000 光年。
    17. (a) 根据上一个问题中的信息，你需要什么速度才能从我们现在的位置逃离银河系？ (b) 你需要将太空飞船加速到相对于地球的这个速度吗？
    18. 方程式 13.10 中圆锥截面的圆轨道的偏心率必须为零。 由此，并使用应用于向心加速度的牛顿第二定律，可以看出方程 13.10 中 α 的值由其\(\alpha = \frac{L^{2}}{GMm^{2}}\)中 L 是轨道物体的角动量给出的。 α的值是恒定的，无论轨道类型如何，都由此表达式给出。
    19. 表明，对于圆锥截面，如果偏心率等于方程 13.10 中的一，则路径是抛物线。 为此，用笛卡尔坐标 x 和 y 代替极坐标 r 和\(\theta\)，并显示它具有抛物线的一般形式 x = ay 2 + 乘以 + c。
    20. 使用 Satell ite Orbits and Energ y 中显示的技术，表明围绕其共同质心的圆形轨道上的两个质量 m 1 和 m 2 将具有总能量\(E = K + E = K_{1} + k_{2} - \frac{Gm_{1} m_{2}}{r} = - \frac{G m_{1} m_{2}}{2r}\)。 我们已经明确显示了两个质量的动能。 （提示：质量分别以半径 r 1 和 r 2 运行，其中 r = r 1 + r 2。 一定不要将向心加速所需的半径与引力所需的半径混淆。）
    21. 给定椭圆轨道的近日点距离 p 和远日点距离，q 表示近日点处的速度 v p 由给出\(v_{p} = \sqrt{\frac{2GM_{Sun}}{(q + p)} \frac{q}{p}}\)。 （提示：使用角动量守恒来关联 v p 和 v q，然后代入能量守恒方程。）
    22. 彗星 P/1999 R1 的近日点为 0.0570 AU，远日点为 4.99 AU。 根据上一个问题的结果，找出它的远日点速度。 （提示：该表达式代表近日点。 使用对称性重写远日点的表达式。）

    挑战问题

    1. 隧道是通过半径为 R 的完美球形无气行星的中心挖出的。使用近地表引力中得出的 g 表达式来获得均匀的密度，表明掉落在隧道中的质量为 m 的粒子将执行简单的谐波运动。 推断 m 的振荡周期，表明它与地表轨道的周期相同。
    2. 按照《近地引力》中使用的技术，求得 g 的值作为半径 r 的函数，该行星密度恒定\(\rho\)且内外半径为 R 的内外半径 R。 为 R in < r < R out 和 r < R in 都找到 g。 假设炮弹内部保持无气状态，请描述一下在球壳行星内部的旅行。
    3. 显示半径为 r 的环形轨道大约质量为 M 的面速为\(\frac{\Delta A}{\Delta t} = \frac{1}{2} \sqrt{GMr}\)。 你的表达式给出了地球绕太阳的面积速度的正确值吗？
    4. 表明两个质量 m 1 和 m 2 在半径分别为 r 1 和 r 2 的圆轨道上围绕其共同质心的轨道周期由其\(T = 2 \pi \sqrt{\frac{r^{3}}{G(m_{1} + m_{2})}}\)中 r = r 1 + r 2 给出。 （提示：质量分别以半径 r 1 和 r 2 运行，其中 r = r 1 + r 2。 使用质心表达式将两个半径关联起来，并注意两个质量必须具有相等但相反的力矩。 从周期与其中一个质量的周长和轨道速度的关系开始。 使用前一个问题的结果，在动能表达式中使用 momenta。）
    5. 表明，对于身高 h 的微小变化，例如 h << R E，方程 13.4 简化为表达式\(\Delta\) U = mgh。
    6. 使用图 13.9，仔细绘制一个悬挂在纬度 lambda 处的简单摆锤的自由体图，标记作用于点质量 m 的所有力。设置平衡运动方程，在向心加速度方向（图中朝向 P）设置一个坐标，另一个垂直于此。 显示偏转角\(\epsilon\)度（定义为摆弦和朝向地球中心的径向方向之间的角度）由以下表达式给出。 纬度 45 度的偏转角是多少？ 假设地球是一个完美的球体。 \(\tan(\lambda + \epsilon) = \frac{g}{(g − \omega^{2} R_{E})} \tan \lambda\)，其中\(\omega\)是地球的角速度。
    7. (a) 表明质量为 m 的小物体上的潮汐力由 F tidal =\(\frac{2GMm}{R^{3}} \Delta\) r 给出，其定义是由于距离 M 的距离 R 处的引力而在物体近端和远端一定距离处施加在 m 上的引力之差，其中\(\Delta\)r 是近边和远边之间的距离，\(\Delta\)r << R。 (b) 假设你先掉入银河系中心的黑洞。 它的质量为400万个太阳质量。 你的头部力量和施瓦茨柴尔德半径（事件视野）处的脚部力量有什么区别？ 假设你的脚和头各有 5.0 kg 的重量，相距 2.0 m。 你能在事件视野中幸存下来吗？
    8. 找到火星旅行所需的霍曼传递速度\(\Delta\) v EllipseEarth 和\(\Delta\) v EllipseMar s。 使用方程式 13.7 求出地球和火星的圆轨道速度。 使用方程 13.4 和由 E = −\(\frac{GmM_{s}}{2a}\) 给出的椭圆（半长轴 a）的总能量，求出传递椭圆上所需的地球（近日点）和火星（远日点）的速度。 每个点的差\(\Delta\) v 是所需的速度提升或传输速度。

    贡献者和归因

    Template:ContribOpenStaxUni