13.8: 爱因斯坦的引力理论
- Page ID
- 204531
- 描述广义相对论是如何处理引力的
- 解释等价原理
- 计算物体的 Schwarzschild 半径
- 总结黑洞的证据
牛顿的万有引力定律准确地预测了我们在太阳系中看到的大部分内容。 事实上,只需要牛顿定律就能准确地将所有太空飞行器送上行程。 只有牛顿定律才能精确确定穿越地球的小行星和大多数其他天体的路径。 尽管如此,许多现象显示出与牛顿定律所预测的差异,包括水星的轨道和重力对光的影响。 在本节中,我们将研究设想引力的另一种方法。
视角革命
1905 年,爱因斯坦发表了他的狭义相对论。 相对论中详细讨论了这个理论,所以我们在这里只说几句话。 在这个理论中,任何运动都不能超过光速——这是宇宙的速度极限。 这个简单的事实已经在无数实验中得到证实。 但是,它会带来难以置信的后果——空间和时间不再是绝对的。 两个人相对于彼此移动,在物体的长度或时间的流逝上没有共识。 你在前几章中学到的几乎所有机制,虽然即使在数千英里/秒的速度下也非常准确,但在接近光速时就会开始失效。
对宇宙的这种速度限制也是对牛顿引力定律中固有的假设的挑战,即重力是一种远距离作用的力。 也就是说,在没有身体接触的情况下,一个质量体位置的任何变化都会立即传达给所有其他质量。 这个假设并非来自任何第一原则,因为牛顿的理论根本没有解决这个问题。 (人们对电磁力的看法也是如此。 可以公平地说,大多数科学家对远距离行动的概念并不完全满意。)
第二个假设也出现在牛顿引力定律方程 13.2.1 中。 假定质量与牛顿第二定律中使用的质量完全相同,\(\vec{F}\)= m\(\vec{a}\)。 我们在本章的许多推导中都做出了这样的假设。 同样,没有必须这样做的基本原则,但实验结果与这一假设一致。 在爱因斯坦随后的广义相对论(1916)中,这两个问题都得到了解决。 他的理论是关于时空几何以及质量(和加速度)如何扭曲和与时空相互作用的理论。 这不是引力理论。 一般理论的数学超出了本文的范围,但我们可以看一些基本原理及其后果。
等价原理
爱因斯坦得出通论的部分原因是想知道为什么自由落体的人没有感觉到自己的体重。 事实上,人们常说绕地球轨道运行的宇航员失重,尽管那里的地球重力仍然很强。 在爱因斯坦的通论中,自由落体和失重之间没有区别。 这称为等价原理。 同样令人惊讶的必然结果是,在没有重力的情况下,均匀的引力场和均匀的加速度之间没有区别。 让我们重点谈谈最后一句话。 尽管完全均匀的引力场不可行,但我们可以很好地近似它。
在地球上规模合理的实验室中,引力场基本上\(\vec{g}\)是均匀的。 推论指出,在那里进行的任何物理实验的结果都与在远离所有其他质量的深空加速的实验室\(\vec{a} = \vec{g}\)中进行的实验结果相同。 该图\(\PageIndex{1}\)说明了这个概念。
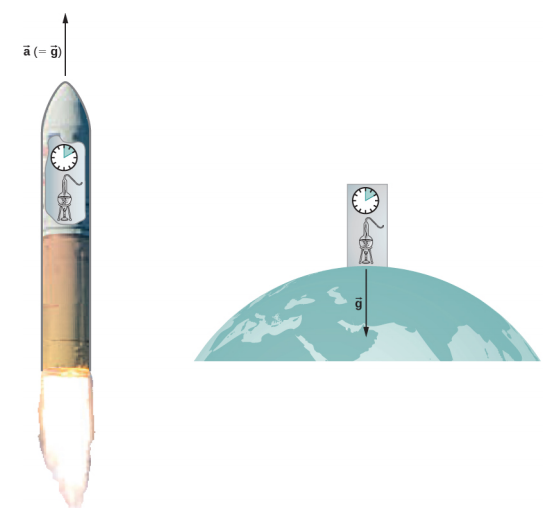
这两种看似根本不同的情况怎么可能是一样的? 答案是,引力不是两个物体之间的力,而是每个物体响应另一个物体对其周围时空的影响的结果。 均匀的引力场和均匀的加速度对时空的影响完全相同。
引力的几何理论
欧几里得几何假设一个 “平坦” 空间,在该空间中,在最常见的已知属性中,直线是两点之间的最短距离,所有三角形的角度之和必须为 180 度,平行线从不相交。 直到十九世纪,才认真研究@@ 非欧几里得几何学,因此,牛顿的所有定律都固有假设欧几里得空间也就不足为奇了。
广义相对论挑战了这个长期存在的假设。 只有空白空间是平坦的。 质量或能量的存在,因为相对论无法区分两者,因此会扭曲或曲线周围的空间和时间或时空。 任何其他质量的运动只是对这个弯曲的时空的响应。 图\(\PageIndex{2}\)是一个二维表示,一个较小的质量随着较大质量的存在而产生的扭曲空间而在轨道运行。 在一幅更精确但令人困惑的画面中,我们还会看到空间被轨道质量扭曲,两个质量都会随着空间的完全失真而运动。 请注意,该图是帮助可视化概念的表示形式。 这些是我们三维空间和时间的扭曲。 我们不像对待球上的酒窝那样看待它们。 只有仔细测量物体和光线在空间中移动时的运动,我们才能看到失真。

对于弱引力场,广义相对论的结果与牛顿的引力定律没有显著差异。 但是对于强引力场,结果各不相同,广义相对论已被证明可以预测正确的结果。 即使在距离水星轨道距离的太阳相对较弱的引力场中,我们也可以观察到其影响。 从1800年代中期开始,已经对水星的椭圆轨道进行了仔细测量。 但是,尽管它是椭圆的,但由于椭圆的近日点位置缓慢移动,它的运动变得复杂。 大部分进步归因于其他行星的引力,但牛顿定律无法解释这种进步的一小部分。 有一次,甚至有人在寻找可以解释这种差异的 “同伴” 行星。 但是广义相对论可以正确预测测量结果。 从那时起,许多测量结果,例如太阳对远处物体的光的偏转,都证实了广义相对论可以正确预测观测结果。
我们最后发表一条评论来结束本次讨论。 我们经常提到时空的扭曲或时空的扭曲。 在狭义相对论和广义相对论中,时间维度与每个空间维度具有同等地位(它在两种理论中的位置只有一个最终不重要的缩放因子不同)。 在非常大的物体附近,不仅附近的空间 “伸展”,而且时间会扩张或 “变慢”。 我们将在下一节中详细讨论这些影响。
黑洞
爱因斯坦的引力理论用一个看似简单的张量方程(张量是标量和向量的概括)来表达,它表示质量如何决定其周围的时空曲率。 这个方程的解得出了最引人入胜的预测之一:黑洞。 预测是,如果一个物体足够密集,它就会自身崩溃,并被一个任何东西都无法逃脱的事件视野所包围。 天文学家约翰·惠勒在1969年创造的 “黑洞” 这个名字指的是光无法逃脱这样的物体这一事实。 卡尔·施瓦茨柴尔德是1916年第一个注意到这种现象的人,但当时,人们认为它主要是出于数学上的好奇心。
令人惊讶的是,光线无法逃脱的巨大物体的想法可以追溯到1700年代后期。 约翰·米歇尔和皮埃尔·西蒙·拉普拉斯独立使用牛顿的引力定律表明,离开具有足够质量的恒星表面的光无法逃脱。 他们的工作基于这样一个事实,即奥莱·罗默在 1676 年测量了光速。 他注意到关于木星的月球艾奥轨道周期的数据存在差异。 罗默意识到,这种差异源于地球和木星在不同时期的相对位置,他可以从这种差异中找到光速。 Michell 和 Laplace 都意识到,由于光的速度有限,因此可能会有一颗足够大的恒星,以至于其表面的逃生速度可能会超过该速度。 因此,光线总是会回落到星星身上。 奇怪的是,距离最大的恒星足够远的观察者无法看见它们,但他们可以从相同的距离看到一颗较小的恒星。
回想一下,在《引力势能》和《总能量》中,我们发现由\(v_{\mathrm{esc}}=\sqrt{\frac{2 G M}{R}}\)给出的逃生速度与逃跑物体的质量无关。 尽管当时还没有完全理解光的本质,但光的质量(如果有的话)并不重要。 因此,这个方程应该对光有效。 用 c,光速,代替逃逸速度,我们有
\[v_{esc} = c = \sqrt{\dfrac{2GM}{R}} \ldotp\]
因此,我们只需要 R 和 M 的值,使逃逸速度超过 c,这样光就无法逃脱。 米歇尔认为,如果一颗恒星的密度相当于我们的太阳,并且半径刚好延伸到火星轨道之外,那么光将无法从其表面逃脱。 他还推测,我们仍然能够从它对周围物体的引力效应中探测到这样的恒星。 这是一个有见地的结论,因为这正是我们推断当今此类物体存在的方式。 尽管我们还没有,也可能永远不会访问黑洞,但黑洞的间接证据已经变得如此令人信服,以至于很少有天文学家怀疑它们的存在。
在我们研究其中一些证据之前,我们将注意力转向施瓦茨柴尔德对广义相对论张量方程的解。 在该解决方案中出现了一个临界半径,现在称为施瓦茨柴尔德半径(R S)。 对于任何质量 M,如果该质量被压缩到其半径小于 Schwarzschild 半径的程度,则质量将崩溃为奇点,任何经过该半径内的东西都无法逃脱。 一旦进入 R S,时间之箭将所有事物都变成奇点。 (从广义的数学意义上讲,奇点是函数值变为无穷大的地方。 在这种情况下,它是空间中体积为零且质量有限的点。 因此,质量密度和引力能变得无限。) 施瓦茨柴尔德半径由下式给出
\[R_{S} = \dfrac{2GM}{c^{2}} \ldotp \label{13.12}\]
如果你看一下我们的逃逸速度方程式 v esc = c,你会注意到它正好给出了这个结果。 但这仅仅是几个错误假设造成的偶然事故。 其中一个假设是使用了不正确的经典表达式来表示光的动能。 物体必须有多密才能变成黑洞?
计算太阳和地球的施瓦茨柴尔德半径。 将原子核的密度与将地球质量均匀压缩到其施瓦茨柴尔德半径所需的密度进行比较。 原子核的密度约为 2.3 x 10 17 kg/m 3。
策略
我们使用方程\ ref {13.12} 进行此计算。 我们只需要地球和太阳的质量,这是我们从附录D 中给出的天文数据中获得的。
解决方案
代替太阳的质量,我们有
\[R_{S} = \dfrac{2GM}{c^{2}} = \dfrac{2(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(1.99 \times 10^{30}\; kg)}{(3.0 \times 10^{8}\; m/s)^{2}} = 2.95 \times 10^{3}\; m \ldotp\]
这个直径只有大约 6 km。 如果我们使用地球的质量,则得到 R S = 8.85 x 10 −3 m。这是直径小于 2 厘米! 如果我们将地球的质量打包到半径为 R S = 8.85 x 10 −3 m 的球体中,则密度为
\[\rho = \dfrac{mass}{volume} = \dfrac{5.97 \times 10^{24}\; kg}{\dfrac{4}{3} \pi (8.85 \times 10^{-3}\; m)^{3}} = 2.06 \times 10^{30}\; kg/m^{3} \ldotp\]
意义
中子星是已知的最紧凑的物体——在黑洞本身之外。 中子星由中子组成,密度相当于原子核,与许多黑洞一样,它被认为是超新星的残余物,超新星是在生命周期结束时爆炸的恒星。 要从地球上制造一个黑洞,我们必须将其压缩到比中子星高十三个数量级的密度。 这个过程需要难以想象的力量。 没有已知的机制可能导致地球大小的物体变成黑洞。 对于太阳来说,你应该能够证明它必须被压缩到只有原子核的80倍左右的密度。 (注意:一旦质量在其施瓦茨柴尔德半径内被压缩,广义相对论就表明它将崩溃为奇点。 这些计算仅显示了引发崩溃所必须达到的密度。)
考虑一下使地球成为黑洞所需的密度与太阳所需的密度相比。 对于制造黑洞需要什么,你能从这个比较中得出什么结论? 你会指望宇宙有许多质量很小的黑洞吗?
事件视野
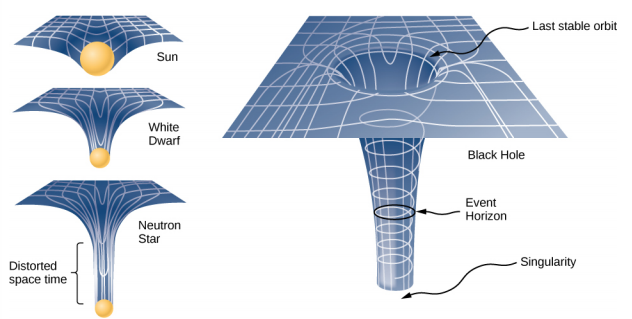
施瓦茨柴尔德半径也被称为黑洞的事件视野。 我们注意到,空间和时间都被拉伸到诸如黑洞之类的大型物体附近。 该图\(\PageIndex{3}\)说明了这种对空间的影响。 太阳造成的失真实际上很小,为了清晰起见,图表被夸大了。 以示例中描述的中子星为例\(\PageIndex{1}\)。 尽管中子星表面的时空失真非常高,但其半径仍然大于其施瓦茨柴尔德半径。 物体仍然可以从其表面逃脱。
但是,如果中子星获得额外的质量,它最终会崩溃,缩小到施瓦茨柴尔德半径之外。 一旦发生这种情况,整个群众将不可避免地被拉到一个奇异的境地。 在图中,空间被拉伸到无穷大。 时间也被拉伸到无穷大。 当物体落向事件视野时,我们看到它们接近的速度越来越慢,但从未到达事件视野。 作为外部观察者,我们永远看不到物体穿过事件视野——实际上,时间被拉长到停顿了。
访问此网站查看这些空间扭曲的动画示例。
黑洞的证据
直到 20 世纪 60 年代,当第一颗中子星被发现时,人们才重新开始对黑洞的存在。 黑洞的证据基于几种类型的观测结果,例如对X射线二进制文件的辐射分析、来自遥远星系的光的引力透镜以及可见物体在隐形伙伴周围的运动。 我们将重点讨论后面的观察结果,因为它们与我们在本章中学到的内容有关。 尽管光无法从黑洞中逃脱出来让我们看见,但我们仍然可以看到黑洞对周围群体的引力效应。
最接近、也许是最引人注目的黑洞证据位于银河系的中心。 加州大学洛杉矶分校银河小组利用W.M. Keck望远镜获得的数据,确定了银河系中心附近几颗恒星的轨道。 其中一些数据如图所示\(\PageIndex{4}\)。 突出显示了两颗恒星的轨道。 根据对其轨道周期和大小的测量,估计它们正在绕大约400万个太阳质量运行。 请注意,质量必须位于由恒星椭圆交点创建的区域中。 该质量必须驻留的区域将位于水星轨道内,但在可见光谱中看不到任何东西。
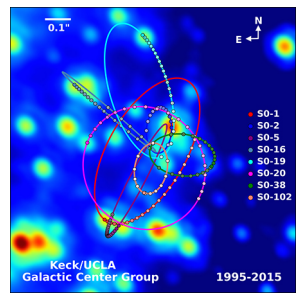
恒星创造和演化的物理学已经很成熟。 使恒星发光的终极能量来源是触发聚变的自引力。 一般的行为是,恒星越大,它发出的光芒越亮,寿命越短。 合乎逻辑的推断是,质量是我们太阳质量的400万倍,局限于一个很小的区域,而且看不见,除了黑洞之外没有其他可行的解释。 银河系外的观测强烈表明,黑洞在星系中心很常见。
访问加州大学洛杉矶分校银河中心小组主页,了解有关 X 射线二进制文件和引力透镜的信息。 访问此页面可查看在银河系中心附近运行的恒星的三维可视化,动画位于页面底部附近。
暗物质
在我们银河系中心附近运行的恒星为那里存在黑洞提供了有力的证据,但是远离中心的恒星轨道表明了另一种有趣的现象,这种现象也是间接观察到的。 回想一下《近地引力》,我们可以考虑球形物体位于中心某一点的质量,以计算它们对其他质量的引力效应。 同样,我们可以将银河系中任何恒星轨道内的总质量视为位于银河系圆盘的中心。 我们可以通过计算可见恒星来估算出该质量,也可以在我们的估计中包括中心黑洞的质量。
但是当我们这样做时,我们发现恒星的轨道速度太快了,不能由这么多的物质引起。 该图\(\PageIndex{5}\)显示了恒星的轨道速度与它们与银河系中心距离的函数。 蓝线代表我们根据对质量的估计所期望的速度,而绿色曲线是我们从直接测量中得到的速度。 显然,有很多我们看不见的物质,估计是我们所见物质的五倍左右,所以它被称为暗物质。 此外,速度曲线不符合我们对观测到的可见恒星分布的预期。 不仅总质量的估计值与数据不一致,而且预期的分布也不一致。 这种现象不仅限于我们的银河系,而且似乎是所有星系的特征。 实际上,这个问题最早出现在20世纪30年代,当时测量星团内的星系绕这些星团的质心运行的速度超过了根据可见质量估计得出的应有速度。
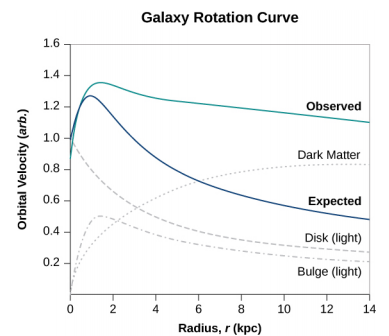
关于这件事可能是什么,有两种普遍的观念:Wimps 和 macHOS。 WIMP 代表弱相互作用的块状粒子。 这些粒子(例如中微子)与普通物质的相互作用非常弱,因此很难直接探测。 MacHOS 代表大型紧凑型光环物体,它们由普通的重子物质组成,例如中子和质子。 这两个想法都存在未解决的问题,要解开这个谜团,还需要进行更多的研究。


