13.7：潮汐力量

Last updated
Save as PDF

Page ID: 204458

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

解释地球海潮的起源
描述 neap 和 leap tides 有何不同
描述潮汐力量如何影响二进制系统

2000多年来，地球海潮的起源一直是持续研究的主题。但是牛顿的工作被认为是真正理解这种现象的开始。海潮是引力潮汐力的结果。任何天体中都存在同样的潮汐力。它们是造成在木星卫星之一艾奥上产生火山活动的内部热量以及离黑洞太近的恒星破裂的原因。

月潮

如果你生活在世界上几乎任何地方的海边，你每天大约可以观察到两次海平面的上升和下降。这是由地球绕其轴线旋转以及月球和太阳的引力共同造成的。

让我们先考虑一下月球的影响。在图中\(\PageIndex{1}\)，我们正在 “向下看” 地球的北极。地球的一侧比另一侧更接近月球，距离等于地球的直径。因此，近侧的引力大于远侧的引力。地球中心的幅度介于这些值之间。这就是为什么地球两边都出现潮汐凸起的原因。

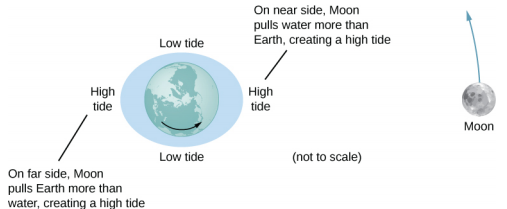
该图是以夸张椭圆为中心的地球的插图，该椭圆的主轴是水平的。月亮显示在地球右侧，逆时针移动。椭圆的左侧被标记为涨潮，上面写着 “在远边，月亮比水更能拉动地球，形成涨潮。” 椭圆的右侧被标记为涨潮，上面写着 “在近边，月亮比地球更能吸引水，形成涨潮。” 椭圆的顶部和底部标有 “退潮”。 — 图\(\PageIndex{1}\)：潮汐力沿着地球和月球之间的线延伸地球。正是从远端到近侧的引力之间的差异在地球两侧造成潮汐凸起。海洋的潮汐变化约为几米；因此，这张图被大大夸大了。

地球上的净力使它绕地月质心运行，该质心位于地球表面下方约1600千米处，沿着地球和月球之间的线路运行。 潮汐力可以看作是地球中心的力与任何其他位置的力之间的差异。在图中\(\PageIndex{2}\)，这种差异显示在海平面上，我们在那里观察海潮。（请注意，这些潮汐力量引起的海平面变化是从基线海平面测量的。我们早些时候看到，由于地球的自转，地球在赤道上凸起了好几公里。这定义了基线海平面，这里我们只考虑从该基线海平面测得的小得多的潮汐凸起。）

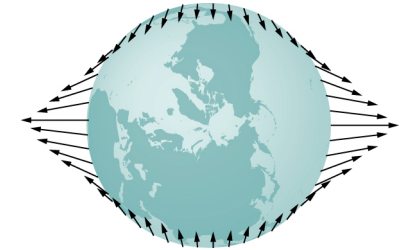
地球和潮汐力量的插图，以箭头的形式显示在地球表面。在两极附近，箭头很短，径向内指向。当我们远离极点时，箭头会变长，指向越来越远离中心。在 45 度处，箭头与表面相切并指向赤道。在赤道处，箭头最长，直接指向外方。 — 图\(\PageIndex{2}\)：潮汐力是中心引力与其他地方的引力之差。在此图中，潮汐力显示在海面。当你接近地球中心时，这些力将减少到零。

为什么潮汐的上升和下降每天发生两次？再看图\(\PageIndex{1}\)。如果地球没有旋转并且月球是固定的，那么凸起将保持在地球上的相同位置。相对于月球，凸起保持固定，沿着连接地球和月球的线路。但是地球大约每 24 小时旋转一次（按照蓝色箭头所示的方向）。 6小时后，地球的近处和远处移动到发生退潮的地方，6小时后，这些位置又回到了涨潮位置。由于月球大约每28天绕地球运行一次，并且其旋转方向与地球旋转的方向相同，因此高（和低）潮之间的时间实际上约为12.5小时。潮汐的实际时间因许多因素而变得复杂，其中最重要的是另一个天体——太阳。

太阳对潮汐的影响

除了月球对地球海洋的潮汐力外，太阳还施加潮汐力。太阳对地球上任何物体的引力吸引力几乎是月球的200倍。但是，正如我们稍后在示例中显示的那样，太阳的潮汐效应小于月球的潮汐效应，但仍然是一个显著的影响。根据月球和太阳相对于地球的位置，净潮汐效应可以放大或减弱。

该图\(\PageIndex{1}\)说明了产生最大潮汐的太阳和月亮的相对位置，称为春潮（或跳潮）。在春季潮汐期间，地球、月球和太阳对齐，潮汐效应会增加。（回想一下，潮汐力量会导致两侧凸起。）该图\(\PageIndex{1c}\)显示了最小潮汐的相对位置，称为 neap tides。涨潮和低潮的极端情况都会受到影响。春潮发生在新月或满月期间，潮汐发生在半月。

模拟

你可以看到一两个关于潮汐运动的动画。

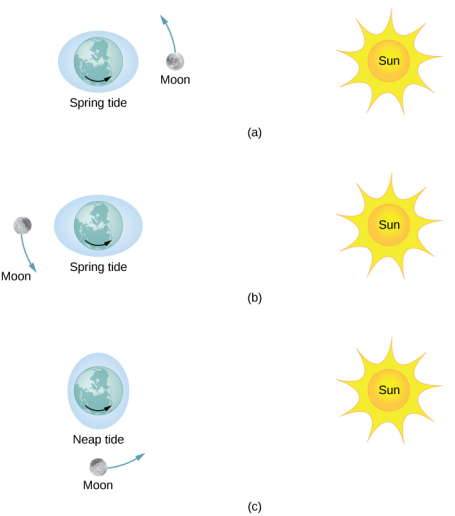
图 a 显示了以标有春潮的水平阴影椭圆为中心的地球。太阳位于地球右侧，月亮排成一行，位于地球和太阳之间，逆时针运行。图 b 显示了以标有春潮的水平阴影椭圆为中心的地球。太阳位于地球的右边，月亮与地球和太阳对齐，但在地球的左边，逆时针运行。图 c 显示了以标有 neap Tide 的垂直阴影椭圆为中心的地球。太阳位于地球右侧，月亮位于地球下方，逆时针运行。部分 c 中的椭圆的垂直长轴明显小于部分 a 和 b 中椭圆的水平长轴。 — 图\(\PageIndex{3}\)：（a 和 b）春季潮汐发生在太阳和月亮对齐时，而（c）当太阳和月亮与地球形成直角三角形时，就会出现整齐的潮汐。（图未按比例绘制。）

潮汐的强度

有了月球和太阳位置的准确数据，就可以准确预测地球上大多数位置的最大和最小潮汐时间。

访问此网站，在美国 3000 多个地点生成过去或未来长达 2 年的潮汐预测。

但是，潮汐的规模要复杂得多。地球和月球的相对角度决定了春季和整齐的潮汐，但这些潮汐的大小也受到与地球距离的影响。距离较小时，潮汐力会更大。月球绕地球的轨道和地球绕太阳的轨道都是椭圆形的，因此，如果春潮发生在月球近地点而地球处于近日点时，则春潮会特别大。相反，如果它发生在月球处于远地点而地球处于远日点时，则相对较小。

潮汐变化的最大原因是当地海岸线的地形和海底的测深（深度剖面）。这些影响造成的潮汐范围令人震惊。尽管全球许多地方的海潮都比一米小得多，但加拿大东海岸芬迪湾（图\(\PageIndex{4}\)）的潮汐可能高达16.3米。

芬迪湾同一个码头的两张照片，似乎是从同一地点拍摄的。左边的照片是在水位很高、水线在附近、船只都漂浮在水中时拍摄的。右边的照片是在水位低时拍摄的。水线很远，船只停在泥里。 — 图\(\PageIndex{4}\)：涨潮和退潮时芬迪湾的船只。海平面每天两次的变化给船只的安全系泊带来了真正的挑战。（来源：Dylan Kereluk）

示例\(\PageIndex{1}\): Comparing Tidal Forces

比较一下月球在位于地球近侧的1.0千克质量和另一个位于地球另一侧的重力上的引力。对太阳重复此操作，然后比较结果，确认月球的潮汐力大约是太阳的两倍。

策略

我们使用方程 13.2.1 给出的牛顿引力定律。我们需要月球和太阳的质量及其与地球的距离，以及地球的半径。我们使用附录 D 中的天文数据。

解决方案

用月球的质量和从地球到月球的平均距离代替，我们有

\[F_{12} = G \frac{m_{1} m_{2}}{r^{2}} = (6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2}) \Bigg[ \frac{(1.0\; kg)(7.35 \times 10^{22}\; kg)}{(3.84 \times 10^{8} \pm 6.37 \times 10^{6}\; m)^{2}} \Bigg] \ldotp\]

在分母中，我们使用负号表示近边，使用加号表示远边。结果是

\[F_{near} = 3.44 \times 10^{-5}\; N\; and\; F_{far} = 3.22 \times 10^{-5}\; N \ldotp\]

月球在地球近侧的引力比远端高出近7％，但是在1.0千克质量上，这两种力都远小于地球本身的引力。尽管如此，这种微小的差异造成了潮流。我们现在重复这个问题，但用太阳的质量和地球与太阳之间的平均距离代替。结果是

\[F_{near} = 5.89975 \times 10^{-3}\; N\; and\; F_{far} = 5.89874 \times 10^{-3}\; N \ldotp\]

我们必须保留六位有效数字，因为我们希望将它们之间的差异与月球的差异进行比较。（尽管我们无法证明该精度的绝对值是合理的，但由于计算中除距离之外的所有值都相同，因此差异中的精度对三位数仍然有效。）由月球引起的 1.0 千克质量上的近距离和远力之间的区别是

\[F_{near} = (3.44 \times 10^{-5}\; N) - (3.22 \times 10^{-5}\; N) = 0.22 \times 10^{-5}\; N,\]

而太阳的区别是

\[F_{near} - F_{far} = (5.89975 \times 10^{-3}\; N) - (5.89874 \times 10^{-3}\; N) = 0.101 \times 10^{-5}\; N \ldotp\]

请注意，更正确的方法是写出两种力的差异，并明确表示近距离和远距离之间的差异。只要用一点代数我们就能证明这一点

\[F_{tidal} = \frac{GMm}{r_{1}^{2}} - \frac{GMm}{r_{2}^{2}} = GMm \left(\dfrac{(r_{2} - r_{1})(r_{2} + r_{1})}{r_{1}^{2} r_{2}^{2}} \right) \ldotp\]

其中 r ₁ 和 r ₂ 等于三个有效数字，但它们的差（r ₂ − r ₁）（等于地球的直径）也已知为三个有效数字。计算结果相同。如果所需的有效位数超过计算器或计算机上可用的有效位数，则必须使用这种方法。

意义

请注意，太阳施加的力比月球施加的力大近200倍。但是太阳的力差是月球力的一半。这就是潮汐力量的本质。月球具有更大的潮汐效应，因为月球从近侧到远端的距离的分数变化要比太阳大得多。

练习\(\PageIndex{1}\)

地球对月球施加潮汐力。它大于、等于还是小于地球上月球的月球？反应时要小心，因为潮汐力是由一侧和另一侧之间的引力差异产生的。看看我们对地球上的潮汐力进行的计算，并考虑月球会发生显著变化的值。月球的直径是地球的四分之一。由于月球表面没有液体，因此不容易探测到月球上的潮汐力。

其他潮汐效应

任何两个物体之间都存在潮汐力。该效果沿着物体中心之间的线拉伸。尽管每天都能观察到潮汐对地球海域的影响，但长期后果并不容易观察。后果之一是物体本身弯曲过程中的摩擦会消耗旋转能量。随着潮汐力将旋转能量转移到热量中，地球的自转速度正在减慢。与角动量的这种耗散和守恒有关的另一种效应被称为 “锁定” 或潮汐同步。太阳系中的大多数卫星，包括地球的月球，都已经发生过这种情况。月球保持一面朝向地球 —— 它的旋转速度已锁定在绕地球的轨道速率中。同样的过程正在发生在地球上，最终它将保持一张脸朝向月球。如果真的发生这种情况，我们将再也看不到潮汐了，因为潮汐凸起将停留在地球上的同一个地方，一半的地球将永远看不到月球。但是，这种锁定将花费数十亿年的时间，也许不是在我们的太阳到期之前。

潮汐效应的一个更引人注目的例子是在木星的卫星之一艾奥身上发现的。 1979 年，旅行者号航天器发回了艾奥火山活动的戏剧性图像。它是我们太阳系中唯一发现这种活动的天体。该图\(\PageIndex{5}\)显示了 “新视野” 号航天器在前往冥王星途中使用木星的重力辅助拍摄的艾奥的最新照片。

艾奥火山喷发的照片。 — 图\(\PageIndex{5}\)：在 Io 上可以看到潮汐力量的戏剧性证据。蓝色的喷发是由于木星对艾奥施加的潮汐力所产生的内部热量造成的。

对于某些恒星来说，潮汐力的影响可能是灾难性的。一旦潮汐力超过了将恒星凝聚在一起的凝聚力自引力，非常接近的二进制系统中的潮汐力就足够强大，足以将物质从一颗恒星撕裂到另一颗恒星。这种效果可以在绕紧凑型恒星运行的普通恒星中看到，例如中子星或黑洞。该图\(\PageIndex{6}\)显示了一位艺术家对这个过程的演示。当物质落入紧凑型恒星时，它会形成一个吸积盘，该吸积盘会变得过热并在X射线光谱中辐射。

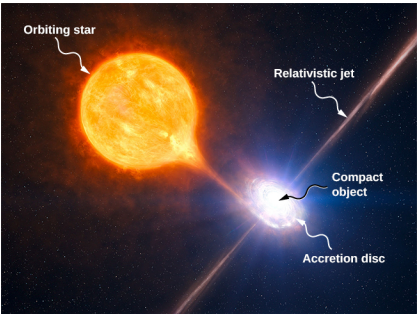
紧凑型物体从轨道恒星中积聚的插图。在小型紧凑物体附近显示了一颗大恒星。显示发光物质被从恒星中拉出，变成一个标有 Accretion 盘的螺旋形物体，在紧凑的物体上盘旋。一条垂直于圆盘的亮线从紧凑物体的中心延伸到上方和下方，并被标记为相对论射流。 — 图\(\PageIndex{6}\)：来自紧凑物体的潮汐力可以将物质从轨道恒星上撕掉。如图所示，除了围绕紧凑物体运行的吸积盘外，物质还经常沿着相对论喷气机喷射。（来源：欧洲南方天文台（ESO）对作品的修改）

这些二进制系统的能量输出可能超过数千颗恒星的典型输出。另一个例子可能是类星体。类星体是非常遥远且非常明亮的物体，通常超过整个星系的能量输出。天文学家的普遍共识是，它们实际上是产生辐射能量的巨大黑洞，因为从附近恒星上潮汐撕下的物质落入其中。