13.6: 开普勒行星运动定律
- Page ID
- 204529
- 描述圆锥截面及其与轨道运动的关系
- 描述轨道速度与角动量守恒的关系
- 确定椭圆轨道从其长轴开始的周期
约翰内斯·开普勒利用第谷·布拉赫收集的精确数据,仔细分析了所有已知行星和月球在天空中的位置,定期绘制它们的位置。 根据这一分析,他制定了三条法律,我们将在本节中讨论这些法律。
开普勒第一定律
开普勒时代的普遍看法是,所有行星轨道都是圆形的。 火星的数据对这种观点提出了最大的挑战,最终促使开普勒放弃了这个流行的想法。 开普勒的第一定律指出,每颗行星都沿着椭圆移动,太阳位于椭圆的焦点处。 椭圆被定义为所有点的集合,因此从每个点到两个焦点的距离之和是一个常数。 图中\(\PageIndex{1}\)显示了一个椭圆并描述了创建椭圆的简单方法。
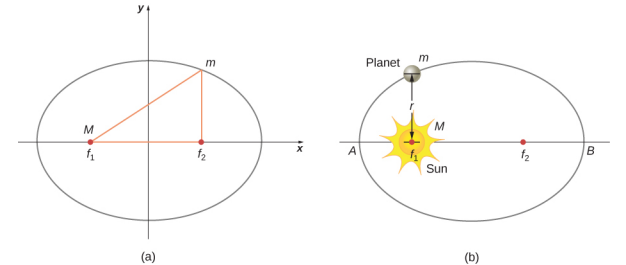
对于椭圆轨道,行星最接近太阳的点称为近日点。 它在图中被标记为点 A\(\PageIndex{1}\)。 最远的点是远日点,在图中被标记为点 B。 对于月球绕地球的轨道,这些点分别被称为近地点和远地点。
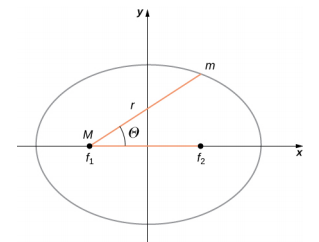
椭圆有几种数学形式,但它们都是更通用的圆锥截面方程的具体例子。 有四个不同的圆锥截面,全部由方程给出
\[\frac{\alpha}{r} = 1 + e \cos \theta \ldotp \label{13.10}\]
如果\(\theta\)是椭圆,则变量\(r\)和如图\(\PageIndex{2}\)所示。 常数 α 和 e 由卫星在给定点的总能量和角动量决定。 常数 e 称为偏心率。 \(\alpha\)和 e 的值决定了四个圆锥截面中哪一个代表卫星的路径。
牛顿万有引力定律(力与距离平方的逆数成正比)的真正胜利之一是,当它与他的第二定律相结合时,任何卫星路径的解都是圆锥截面。 m 所采用的每条路径都是四个圆锥截面之一:表示边界或封闭轨道的圆或椭圆,或者表示无界或开放轨道的抛物线或双曲线。 这些圆锥截面如图所示\(\PageIndex{3}\)。
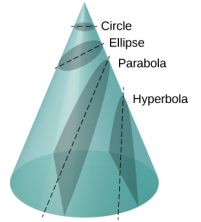
如果总能量为负,则 0 ≤ e < 1,方程\ ref {13.10} 表示椭圆或圆的边界或封闭轨道,其中 e = 0。 [从方程式 13.10 中可以看出,对于 e = 0,r =\(\alpha\),因此半径是恒定的。] 对于椭圆,偏心率与椭圆的长方形长度有关。 圆的偏心率为零,而一个很长的绘制椭圆的偏心率接近于一个偏心率。
如果总能量正好为零,则 e = 1,路径是抛物线。 回想一下,总能量为零的卫星的逃逸速度正好相同。 (抛物线只能通过沿表面切线平行于切线的圆锥体来形成。) 最后,如果总能量为正,则 e > 1,路径为双曲线。 最后两条路径代表无界轨道,其中 m 经过 M 一次,仅一次。 已经观察到几颗彗星的这种情况,这些彗星接近太阳,然后离开,再也不会返回。
我们仅限于较小的质量(行星)绕大得多的质量(太阳)运行的情况,但方程13.10也适用于任何两个引力相互作用的质量。 每个质量都描绘出与另一个质量完全相同的形状的圆锥截面。 该形状由系统的总能量和角动量决定,系统的质心位于焦点处。 两条路径的尺寸之比是其质量之比的逆数。
你可以在 PhET 的 “我的太阳系” 页面上看到两个相互作用的物体的动画。 选择 “太阳和星球” 预设选项。 你也可以查看更复杂的多体问题。 你可能会发现月球的实际路径相当令人惊讶,但它遵守了牛顿的简单运动定律。
轨道传输
自从太阳系的其他行星被发现以来,人们就想过要去这些行星旅行。 但是我们怎样才能最好地做到这一点呢? 最有效的方法是沃尔特·霍曼(Walter Hohmann)在1925年发现的,灵感来自当时的科幻小说。 该方法现在被称为霍曼传输。 对于在两个圆形轨道之间行驶的情况,传递是沿着 “传输” 椭圆进行的,该椭圆完美地拦截了椭圆的远日点和近日点处的轨道。 该图\(\PageIndex{4}\)显示了从地球轨道前往火星轨道的情况。 和以前一样,太阳是椭圆的焦点。
对于任何椭圆,半长轴定义为近日点和远日点之和的一半。 在图中\(\PageIndex{4}\),半长轴是沿 x 轴从原点到椭圆任一侧的距离,或者只是最长轴(称为长轴)的一半。 因此,要从一个半径为 r 1 的圆形轨道行进到另一个半径为 r 2 的圆形轨道,转移椭圆的远日点将等于较大轨道的值,而近日点将是较小的轨道。 因此,表示为 a 的半长轴由给出\(a = \frac{1}{2} (r_{1} + r_{2})\)。
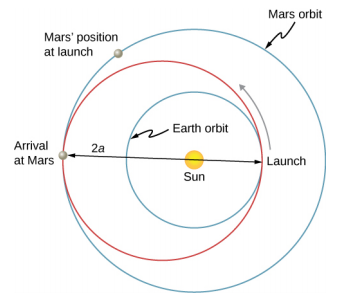
让我们以从地球到火星的旅行为例。 目前,我们忽略了行星,假设我们独自一人在地球轨道上,希望移动到火星轨道。 从方程13.9(总能量的表达式)中,我们可以看出,较大轨道(火星)中航天器的总能量大于较小轨道(地球)的总能量(负值较小)。 要从地球轨道向转移椭圆移动,我们需要增加动能,也就是说,我们需要提高速度。 最有效的方法是沿着圆形轨道进行非常快速的加速,这也是沿着那个点的椭圆路径加速。 (实际上,加速度应该是瞬间的,这样在加速过程中,圆轨道和椭圆轨道是一致的。 实际上,有限加速度足够短,因此差异不是一个重要的考虑因素。) 一旦你到达火星轨道,你需要再次提升速度才能进入该轨道,否则你将停留在椭圆轨道上,然后回到起点的近日点。 对于回程,您只需在每个传输点进行逆向升压即可。
要移动到传递椭圆上然后再次离开,我们需要知道每个圆形轨道速度以及近日点和远日点处的传递轨道速度。 所需的速度提升只是圆轨道速度和每个点的椭圆轨道速度之间的差异。 我们可以从方程13.7中找到圆轨道速度。 为了确定椭圆的速度,我们在没有证据的情况下声明(因为它超出了本课程的范围),椭圆轨道的总能量为
\[E = - \frac{GmM_{S}}{2a}\]
其中 M S 是太阳的质量,a 是半长轴。 值得注意的是,这与圆形轨道的方程13.9相同,但半长轴的值取代了轨道半径。 由于我们知道方程式 13.4 中的势能,因此我们可以找到动能,从而找到椭圆上每个点所需的速度。 我们把寻找地球到火星之旅的传递速度当作一个挑战性问题。
在本次讨论的最后,我们将指出一些重要的细节。 首先,我们没有考虑地球和火星产生的引力势能,也没有考虑在火星上着陆的机制。 实际上,这必须是计算的一部分。 其次,时机决定一切。 你不想在到达火星轨道时发现它不存在。 我们必须精确地在正确的时间离开地球,这样火星才能在我们到达时处于转移椭圆的远日点。 这个机会每两年出现一次。 而且退货也需要正确的时机。 总行程将花费不到3年的时间! 还有其他选项可以更快地过境,包括金星的重力辅助飞越。 但是这些其他选择会带来额外的能量消耗,并给宇航员带来危险。
访问此网站 (https://openstaxcollege.org/l/21plantripmars),了解有关计划火星之旅的更多详细信息。
开普勒第二定律
开普勒第二定律指出,行星在相等的时间内扫出相等的区域,也就是说,除以时间的面积(称为面速)是恒定的。 以图为例\(\PageIndex{5}\)。 行星从 A 位置移动到 B 位置,横扫区域 A 1 所花费的时间,正是从 C 位置移动到 D、扫荡区域 A 2 以及从 E 移动到 F、扫荡区域 A 3 所花费的时间。 这些区域是相同的:A 1 = A 2 = A 3。
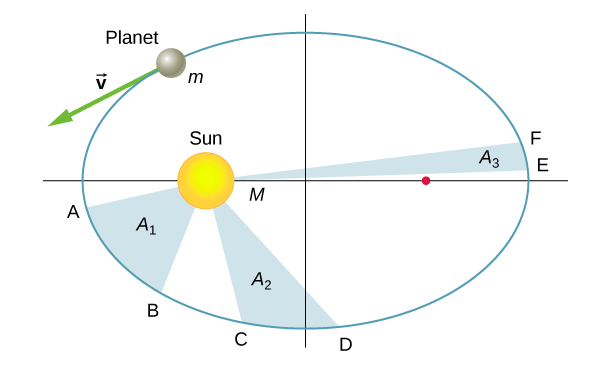
比较图中的面积和每种情况下沿椭圆行进的距离,我们可以看出,为了使面积相等,行星在离太阳越来越近时必须加速,并在移动时减速。 这种行为与我们的守恒方程式\ ref {13.5} 完全一致。 但是我们将证明,开普勒第二定律实际上是角动量守恒的结果,这适用于任何只有径向力的系统。
回想一下角动量中角动量的定义,\(\vec{L} = \vec{r} \times \vec{p}\)。 就轨道运动而言,\(\vec{L}\)是行星绕太阳的角动量,\(\vec{r}\)是从太阳测量的行星的位置矢量,\(\vec{p}\)= m\(\vec{v}\) 是轨道上任何点的瞬时线性动量。 由于行星沿椭圆移动,\(\vec{p}\)因此始终与椭圆相切。
我们可以将线性动量分解为两个分量:\(\vec{p}_{rad}\)沿着通往太阳的线的径向分量和\(\vec{p}_{perp}\)垂直于的分量\(\vec{r}\)。 然后可以将角动量的交叉积写成
\[\begin{align*} \vec{L} &= \vec{r} \times \vec{p} \\[4pt] &= \vec{r} \times (\vec{p}_{rad} + \vec{p}_{perp}) \\[4pt] &= \vec{r} \times \vec{p}_{rad} + \vec{r} \times \vec{p}_{perp} \ldotp \end{align*}\]
右边的第一个项为零,因为它平行\(\vec{r}\)于\(\vec{p}_{rad}\),而在第二个项中垂直\(\vec{r}\)于\(\vec{p}_{perp}\),所以交叉积的大小减小为
\[L = rp_{perp} = rmv_{perp}.\]
请注意,角动量不取决于\(p_{rad}\)。 由于引力仅在径向方向上,因此只能改变\(p_{rad}\)而不能改变\(p_{perp}\);因此,角动量必须保持恒定。
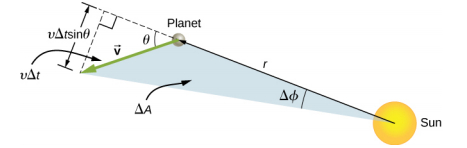
现在考虑图\(\PageIndex{6}\)。 一个小的三角形区域\(\Delta A\)会被及时扫除\(\Delta t\)。 速度沿着路径行驶,它\(\theta\)与径向方向成一个角度。 因此,垂直速度由下式给出\(v_{perp}= v\sin \theta\)。 行星沿着垂直的方向移动距离\(\Delta\) s = v\(\Delta\) ts\(\theta\) in\(r\)。 由于三角形的面积是底数 (\(r\)) 乘以高度 (\(\Delta s\)) 的一半,因此对于小位移,面积由下式给出
\[\Delta A = \frac{1}{2} r \Delta s. \nonumber\]
代替\(\Delta s\),乘\(m\)以分子和分母,然后重新排列,我们得到
\[\Delta A = \frac{1}{2} r \Delta s = \frac{1}{2} r (v \Delta t \sin \theta) = \frac{1}{2m} r (mv \sin \theta \Delta t) = \frac{1}{2m} r (mv_{perp} \Delta t) = \frac{L}{2m} \Delta t \ldotp\]
面速只是面积随时间的变化率,所以我们有
\[ \text{areal velocity} = \frac{\Delta A}{\Delta t} = \frac{L}{2m} \ldotp\]
由于角动量是恒定的,因此面速也必须恒定。 这正是开普勒的第二定律。 与开普勒的第一定律一样,牛顿表明这是他的引力定律的自然结果。
你可以在物理学院(新南威尔士大学)网站上观看 Figur\(\PageIndex{6}\) e 的动画版本以及许多其他有趣的动画。
开普勒第三定律
开普勒第三定律指出,周期的平方与轨道半长轴的立方成正比。 在《卫星轨道与能量》中,我们针对圆形轨道的特殊情况推导了开普勒第三定律。 方程\ ref {13.8} 给出了围绕地球半径为 r 的圆形轨道的周期:
\[T = 2 \pi \sqrt{\frac{r^{3}}{GM_{E}}} \ldotp \label{13.5.5}\]
对于椭圆,回想一下,半长轴是近日点和远日点之和的一半。 对于圆形轨道,半长轴 (\(a\)) 与轨道的半径相同。 实际上,方程\ ref {13.5.5} 如果我们简单地将两边替换\(r\)为平方,就可以得出开普勒的第三定律。\(a\)
\[T^{2} = \frac{4 \pi^{2}}{GM} a^{3} \label{13.11}\]
我们已经将地球的质量改为更一般的地球质量\(M\),因为这个方程适用于绕任何大质量运行的卫星。
确定哈雷彗星轨道的半长轴,因为哈雷彗星每75.3年到达近日点。 如果近日点是 0.586 AU,那么远日点是什么?
策略
我们得到了周期,因此我们可以重新排列方程\ ref {13.11},求解半长轴。 既然我们知道近日点的值,我们可以使用本节前面给出的半长轴的定义来找到远日点。 我们注意到,1 天文单位 (AU) 是地球轨道的平均半径,定义为 1 AU = 1.50 x 10 11 m。
解决方案
重新排列方程\ ref {13.11} 并插入哈雷彗星周期和太阳质量的值,我们有
\[\begin{split} a & = \left(\dfrac{GM}{4 \pi^{2}} T^{2}\right)^{1/3} \\ & = \left(\dfrac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(2.00 \times 10^{30}\; kg)}{4 \pi^{2}} (75.3\; yr \times 365\; days/yr \times 24\; hr/day \times 3600\; s/hr)^{2}\right)^{1/3} \ldotp \end{split}\]
这样,半长轴的值为 2.67 x 10 12 m 或 17.8 AU。 半长轴是远日点和近日点之和的一半,所以我们有
\[\begin{split} a & = \frac{1}{2} (aphelion + perihelion) \\ aphelion & = 2a - perihelion \ldotp \end{split}\]
代替这些值,我们发现半长轴和近日点的给定值,我们发现远日点的值为 35.0 AU。
意义
牛顿的当代人埃德蒙·哈雷首次怀疑1531年、1607年和1682年报道的三颗彗星实际上是同一颗彗星。 在第谷布拉赫对彗星进行测量之前,人们认为它们是一次性事件,可能是大气中的干扰,它们没有受到太阳的影响。 哈雷用牛顿的新机制来预测他的同名彗星将在1758年回归。
土星近乎圆形的轨道的平均半径约为9.5 AU,周期为30年,而天王星的平均半径约为19 AU,周期为84年。 这和我们对哈雷彗星的结果一致吗?


