13.5: 卫星轨道和能量
- Page ID
- 204459
- 描述环形轨道的机制
- 找出卫星的轨道周期和速度
- 确定物体是否受引力约束
月球绕地球运行。 反过来,地球和其他行星绕太阳运行。 我们大气层正上方的空间充满了轨道上的人造卫星。 我们研究了这些轨道中最简单的轨道,即圆形轨道,以了解行星和卫星的速度和周期与其位置和运行的物体之间的关系。
圆形轨道
正如本章开头所述,尼古拉斯·哥白尼首先建议地球和所有其他行星绕太阳绕圈运行。 他进一步指出,轨道周期随着与太阳的距离而增加。 开普勒后来的分析表明,这些轨道实际上是椭圆,但太阳系中大多数行星的轨道几乎是圆形的。 地球与太阳的轨道距离仅相差2%。 唯一的例外是水星的偏心轨道,其轨道距离相差近40%。
对于圆形轨道,确定卫星的轨道速度和轨道周期要容易得多,因此我们在接下来的推导中做出了这样的假设。 正如我们在上一节中所描述的那样,总能量为负的物体受到引力约束,因此进入轨道。 我们对环形轨道特殊情况的计算将证实这一点。 我们专注于绕地球运行的物体,但我们的结果可以概括为其他情况。
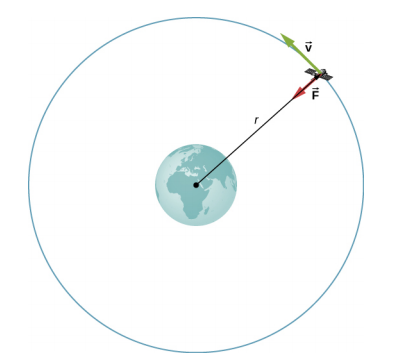
假设一颗质量为 m 的卫星在环绕地球的轨道上,\(r\)距离地球中心很远(图\(\PageIndex{1}\))。 它的向心加速度指向地球中心。 地球的重力是唯一起作用的力,所以牛顿的第二定律给出了
\[\frac{GmM_{E}}{r^{2}} = ma_{c} = \frac{mv_{orbit}^{2}}{r} \ldotp\]
我们求解轨道速度,注意到轨道速度会\(m\)取消,以获得轨道速度
\[v_{orbit} = \sqrt{\frac{GM_{E}}{r}} \ldotp \label{13.7}\]
与我们在\(g = G \frac{M_E}{r^2}\)和中看到的一致性\(v_{esc} = \sqrt{\frac{2GM}{R}}\),m 没有出现在方程式\ ref {13.7} 中。 g 的值、逃逸速度和轨道速度仅取决于与行星中心的距离,而不取决于被作用的物体的质量。 注意 v or b it 和 v esc 的方程有相似之处。 逃逸速度恰好是轨道速度的\(\sqrt{2}\)几倍,约为40%。 示例 13.4.2 中注意到了这种比较,任何半径的卫星都是如此。
为了找到环形轨道的周期,我们注意到卫星在一个周期内沿着轨道\( 2\pi r\)的周长行驶\(T\)。 根据速度的定义,我们有
\[v_{orbit} = \frac{2 \pi r}{T}.\]
我们把它替换成方程\ ref {13.7} 然后重新排列得到
\[T = 2 \pi \sqrt{\frac{r^{3}}{GM_{E}}} \ldotp \label{13.8}\]
我们在下一节中看到,这代表了开普勒针对圆形轨道的第三定律。 它还证实了哥白尼的观察,即行星的周期随着与太阳距离的增加而增加。 我们只需要\(M_{Sun}\)在方程式\ ref {13.8} 中替换\(M_E\)为。
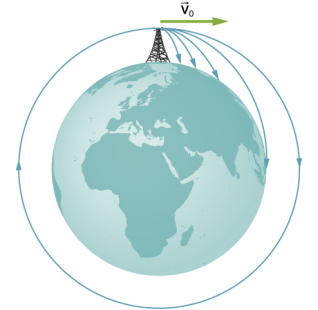
在本节结束时,我们将回到之前的讨论,即轨道上的宇航员似乎失重,好像他们在向地球自由落体一样。 实际上,它们处于自由落体状态。 以图中所示的轨迹为例\(\PageIndex{2}\)。 (这个数字是根据牛顿在他的《Princ ipia》中的一幅画改编的,早些时候也出现在《二维与三维运动》中。) 显示的所有撞击地球表面的轨迹都小于轨道速度。 宇航员将沿着所示的非圆形路径加速向地球,感觉失重。 (实际上,宇航员通过乘坐一次自由落体30秒的飞机在轨道上进行生命训练。) 但是,在正确的轨道速度下,地球表面偏离它们的速度与它们坠落到地球的速度完全相同。 当然,与地表保持相同的距离是圆形轨道的重点。
我们可以在以下问题解决策略中总结我们对轨道卫星的讨论。
- 确定速度、能量或周期等方程对当前问题是否有效。 如果不是,请从我们用来推导这些方程的第一原理开始。
- 要从第一原理开始,绘制一张自由体图,然后应用牛顿引力定律和牛顿第二定律。
- 除了速度和能量的定义外,还将牛顿的第二运动定律应用于感兴趣的物体。
确定国际空间站(ISS)的轨道速度和周期。
策略
由于国际空间站在距离地球表面 4.00 x 10 2 千米处运行,因此其运行半径为 R E + 4.00 x 10 2 km。 我们分别使用方程\ ref {13.7} 和\ ref {13.8} 来计算轨道速度和周期。
解决方案
使用方程\ ref {13.7},轨道速度为
\[v_{orbit} = \sqrt{\frac{GM_{E}}{r}} = \sqrt{\frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(5.96 \times 10^{24}\; kg)}{(6.36 \times 10^{6} + 4.00 \times 10^{5})\; m}} = 7.67 \times 10^{3}\; m/s\]
时速约为 17,000 英里/小时。 使用方程\ ref {13.8},周期为
\[T = 2 \pi \sqrt{\frac{r^{3}}{GM_{E}}} = 2 \pi \sqrt{\frac{(6.36 \times 10^{6} + 4.00 \times 10^{5}\; m)^{3}}{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(5.96 \times 10^{24}\; kg)}} = 5.55 \times 10^{3}\; s\]
刚刚超过 90 分钟。
意义
国际空间站被认为处于低地球轨道(LEO)。 几乎所有卫星都在低地轨道上,包括大多数气象卫星。 全球定位系统卫星位于大约20,000公里处,被认为是中地球轨道。 轨道越高,放置轨道所需的能量就越多,到达轨道进行维修所需的能量也就越多。 特别令人感兴趣的是地球同步轨道上的卫星。 地面上所有指向天空的固定卫星天线,例如电视接收天线,都指向地球同步卫星。 这些卫星被放置在精确的距离上,并且正好位于赤道上方,因此它们的轨道周期为1天。 它们相对于地球表面的固定位置保持不变。
必须通过什么因素改变半径才能将卫星的轨道速度降低一半? 这会通过什么因素改变时期?
从月球轨道确定地球的质量。
策略
我们使用方程\ ref {13.8},求解 M E,然后代替轨道的周期和半径。 月球轨道的半径和周期是几千年前以合理的精度测量的。 根据附录D 中的天文数据,月球的周期为27.3天=2.36 x 10 6 秒,地球中心和月球中心之间的平均距离为384,000千米。
解决方案
求解\(M_E\),
\[\begin{split} T & = 2 \pi \sqrt{\frac{r^{3}}{GM_{E}}} \\ M_{E} & = \frac{2 \pi^{2} r^{3}}{GT^{2}} = \frac{4 \pi^{2} (3.84 \times 10^{8}\; m)^{3}}{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(2.36 \times 10^{6}\; s)^{2}} = 6.01 \times 10^{24}\; kg \ldotp \end{split}\]
意义
将其与我们在示例 13.3.3 中使用地球表面的值获得的 5.96 x 10 24 kg\(g\) 的值进行比较。 尽管这些值非常接近(~ 0.8%),但两个计算都使用平均值。 g 的值从赤道到极点的变化约为 0.5%。 但是月球有一个椭圆轨道,其中 r 的值变化略高于 10%。 (满月的表观大小实际上差异差不多,但通过偶然的观察很难注意到,因为从一个极端到另一个极端的时间需要好几个月。)
最后一次计算 M E 还有另一个考虑因素。 我们得出方程\ ref {13.8} 假设卫星绕天体中心运行,其半径与它们之间的引力表达式中使用的半径相同。 做了什么假设来证明这一点是合理的? 地球的质量大约是月球的81倍。 月球是否围绕地球的确切中心运行?
让我们重温一下示例 13.2.2。 假设银河系和仙女座星系彼此处于环形轨道上。 每个的速度是多少,它们的轨道周期会有多长? 假设每个太阳质量为8000亿个太阳质量,并且它们的中心相隔250万光年。
策略
我们不能直接使用方程\ ref {13.7} 和\ ref {13.8},因为它们是假设质量物体 m 绕质量更大 M 的行星的中心运行而得出的。我们在示例 13.2.2 中使用牛顿的万有引力定律确定了引力。 我们可以使用应用于任一星系的向心加速度的牛顿第二定律来确定它们的切向速度。 根据这个结果,我们可以确定轨道周期。
解决方案
在示例 13.2.2 中,我们发现星系之间的力为
\[F_{12} = G \frac{m_{1} m_{2}}{r^{2}} = (6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})\frac{[(800 \times 10^{9})(2.0 \times 10^{30})\; kg]^{2}}{[(2.5 \times 10^{6})(9.5 \times 10^{15})\; m]^{2}} = 3.0 \times 10^{29}\; N\]
而且每个星系的加速度是
\[a = \frac{F}{m} = \frac{3.0 \times 10^{29}\; N}{(800 \times 10^{9})(2.0 \times 10^{30})\; kg} = 1.9 \times 10^{-13}\; m/s^{2} \ldotp\]
由于星系处于圆形轨道上,因此它们具有向心加速度。 如果我们忽略其他星系的影响,那么,正如我们在《线性动量和碰撞》和《固定轴旋转》中学到的那样,这两个星系的质心保持不变。 因此,星系必须围绕这个共同的质心运行。 对于相等的质量,质心恰好在它们之间的一半。 因此,轨道 r 轨道的半径与星系之间的距离不同,而是该值的一半,即 125 万光年。 这两个不同的值如图所示\(\PageIndex{3}\)。

使用向心加速度的表达式,我们有
\[\begin{split} a_{c} & = \frac{v_{orbit}^{2}}{r_{orbit}} \\ 1.9 \times 10^{-13}\; m/s^{2} & = \frac{v_{orbit}^{2}}{(1.25 \times 10^{6})(9.5 \times 10^{15})\; m} \ldotp \end{split}\]
求解了轨道速度,我们有了\(v_{orbit} = 47\, km/s\)。 最后,我们可以直接从中确定轨道周期
\[T = \frac{2 \pi r}{v_{orbit}}\]
发现周期为 T = 1.6 x 10 18 秒,大约 500 亿年。
意义
起初,47 km/s 的轨道速度可能看起来很高。 但是这个速度与我们在前面的例子中计算的逃离太阳的速度相当。 为了给出更多的视角,这段时间比宇宙存在的时间长了将近四倍。
实际上,这两个星系目前的相对运动如此之大,预计它们将在大约40亿年后发生碰撞。 尽管每个星系中恒星的密度使得任何两颗恒星不太可能直接碰撞,但这种碰撞将对星系的形状产生巨大影响。 这种碰撞的例子在天文学中是众所周知的
星系不是单一物体。 一个星系施加在另一个星系中 “更近” 的恒星上的引力与更远的恒星相比如何? 这会对星系本身的形状产生什么影响?
使用这个交互式模拟来移动太阳、地球、月球和空间站,以查看对它们的引力和轨道路径的影响。 可视化不同天体之间的大小和距离,然后关闭重力,看看没有重力会发生什么。
环形轨道中的能量
在《引力势能》和《总能量》中,我们认为,如果物体的总能量为负,则物体会受到引力约束。 该论点基于一个简单的案例,即速度直接偏离或朝向地球。 我们现在检查圆形轨道的总能量,结果表明,总能量确实是负的。 正如我们之前所做的那样,我们从适用于圆形轨道的牛顿第二定律开始,
\[\begin{split} \frac{GmM_{E}}{r^{2}} & = ma_{c} = \frac{mv^{2}}{r} \\ \frac{GmM_{E}}{r} & = mv^{2} \ldotp \end{split}\]
在最后一步中,我们在两\(r\)边都乘以。 右边只有动能的两倍,所以我们有
\[K = \frac{1}{2} mv^{2} = \frac{GmM_{E}}{2r} \ldotp\]
总能量是动能和势能的总和,所以我们的最终结果是
\[E = K + U = \frac{GmM_{E}}{2r} - \frac{GmM_{E}}{r} = - \frac{GmM_{E}}{2r} \ldotp \label{13.9}\]
我们可以看到,总能量是负的,与动能的大小相同。 对于圆形轨道,动能的大小恰好是势能量的一半。 值得注意的是,这个结果适用于围绕其共同质心的圆形轨道上的任意两个质量,彼此之间的距离为 r。 这方面的证据留作练习。 我们将在下一节中看到,一个非常相似的表达式适用于椭圆轨道。
在示例 13.4.1 中,我们计算了简单地将 9000 千克的联盟号飞行器从地球表面提升到离地面 400 千米的国际空间站高度所需的能量。 换句话说,我们发现它的势能发生了变化。 我们现在要问,联盟号飞行器需要多少总能量变化才能将其从地球表面带走,并将其送入与国际空间站的轨道进行会合(图\(\PageIndex{4}\))? 总能量中有多少是动能?
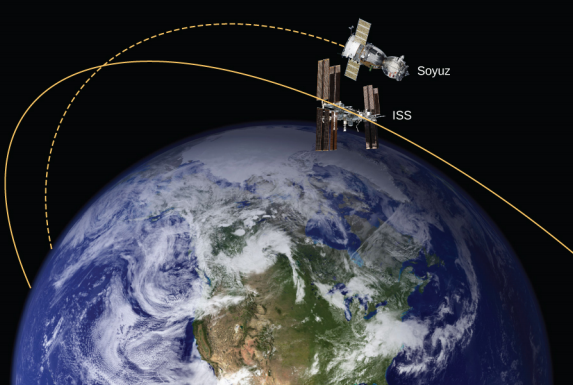
策略
所需的能量是联盟号在轨总能量与地球表面的总能量之差。 我们可以使用方程\ ref {13.9} 来计算联盟号在国际空间站轨道上的总能量。 但是地表的总能量就是势能,因为它是从静止状态开始的。 [请注意,我们不在地表使用方程\ ref {13.9},因为我们不在地表轨道上。] 然后可以从示例 13.4.1 中发现的总能量变化和势能的变化中找到动能。 或者,我们可以使用方程\ ref {13.7} 来找出 v 轨道并直接从中计算动能。 因此,所需的总能量是动能加上示例 13.4.1 中发现的势能变化。
解决方案
根据方程\ ref {13.9},联盟号与国际空间站在同一轨道上的总能量为
\[\begin{split} E_{orbit} & = K_{orbit} + U_{orbit} = - \frac{GmM_{E}}{2r} \\ & = \frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(9000\; kg)(5.96 \times 10^{24}\; kg)}{2(6.36 \times 10^{6} + 4.00 \times 10^{5}\; m)} = -2.65 \times 10^{11}\; J \ldotp \end{split}\]
地球表面的总能量为
\[\begin{split} E_{surface} & = K_{surface} + U_{surface} = 0 - \frac{GmM_{E}}{r} \\ & = - \frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(9000\; kg)(5.96 \times 10^{24}\; kg)}{(6.36 \times 10^{6}\; m)} \\ & = -5.63 \times 10^{11}\; J \ldotp \end{split}\]
能量的变化是
\[\Delta E = E_{orbit}− E_{surface} = 2.98 x 10^{11}\, J. \nonumber\]
为了获得动能,我们从示例 13.4.1 中减去势能的变化,\(\Delta\)U = 3.32 x 10 10 J。这就得出了 K 轨道 = (2.98 x 10 11) − (3.32 x 10 10) = 2.65 x 10 11 J。如前所述,动能的圆形轨道始终是势能量的一半,与总能量的大小相同。 我们的结果证实了这一点。
第二种方法是使用方程式\ ref {13.7} 来找出联盟号的轨道速度,我们在示例中为国际空间站做了同样的事情\(\PageIndex{1}\)。
\[ \begin{align*} v_{orbit} &= \sqrt{\frac{GM_{E}}{r}} \\[4pt]&= \sqrt{\frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(5.96 \times 10^{24}\; kg)}{(6.36 \times 10^{6} + 4.00 \times 10^{5})\; m}} \\[4pt] &= 7.67 \times 10^{3}\; m/s \end{align*}\]
因此,在轨联盟号的动能是
\[ \begin{align*}K_{orbit} &= \frac{1}{2} mv_{orbit}^{2} \\[4pt]&= \frac{1}{2} (9000\; kg)(7.67 \times 10^{3}\; m/s)^{2} \\[4pt]&= 2.65 \times 10^{11}\; J,\end{align*}\]
与前面的方法相同。 总能量只是
\[ \begin{align*}E_{orbit} &= K_{orbit} + \Delta U \\[4pt]&= (2.65 \times 10^{11}) + (3.32 \times 10^{10}) \\[4pt]&= 2.95 \times 10^{11}\; J \ldotp\end{align*}\]
意义
联盟号的动能几乎是其势能变化的八倍,占与国际空间站会合所需总能量的90%。 重要的是要记住,这种能量只代表必须给予联盟号的能量。 根据我们目前的火箭技术,推进系统(火箭燃料、火箭容器和燃烧系统)的质量远远超过有效载荷的质量,必须为该质量提供大量的动能。 因此,实际能量成本是有效载荷本身能量变化的许多倍。


