13.4: 引力势能和总能量
- Page ID
- 204476
- 确定远距离内引力势能的变化
- 应用能量守恒来确定逃逸速度
- 确定天体是否受引力约束
我们在势能和能量守恒中研究了引力势能,其值保持不\(g\)变。 我们现在开发出一种可以在距离上起作用的表达式,因此 g 不是恒定的。 这对于正确计算将卫星送入轨道或将其送入太空任务所需的能量是必要的。
地球以外的引力势能
我们之前定义了工作和潜在能量。 这些定义的用处在于我们可以轻松地使用节能来解决许多问题。 势能对于随位置变化的力特别有用,就像引力在很远的距离上一样。 在《势能与能量守恒》中,我们证明了地球表面附近引力势能的变化是
\[ \Delta U = mg(y_2− y_1) \label{simple}\]
如果在 y 1 和 y 2 之间\(g\)没有显著变化,则效果很好。 我们回到功和势能的定义,得出一个在更远距离内正确的表达式。 回想一下,功率 (W) 是力和距离之间点积的积分。 本质上,它是沿位移的力的分量乘以该位移的乘积。 我们\(\Delta u\)将其定义为与潜在能量相关的力所做工作的负面影响。 为了清楚起见,我们推导出了一个表达式,用于将质量 m 从距离 r 1 从地球中心移动到距离 r 2。 但是,结果可以很容易地概括为任意两个对象将其分离从一个值更改为另一个值。
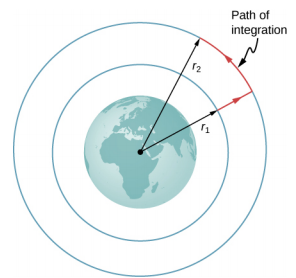
以图为例\(\PageIndex{1}\),其中我们从距地球中心的距离 r 1 取出 m 到距中心 r 2 的距离。 重力是一种保守力(其大小和方向仅是位置函数),因此我们可以选择任何我们想要的路径,计算功率的结果是相同的。 我们采用所示的路径,因为它极大地简化了集成。 我们首先从距离 r 1 向外径向移动到距离 r 2,然后沿着圆的弧线移动,直到到达最终位置。 在径向部分\(\vec{F}\),与我们沿 d 行进的方向相反\(\vec{r}\),所以
\[E = K_1 + U_1 = K_2 + U_2\]
沿着弧线,垂直\(\vec{F}\)于 d\(\vec{r}\),所以\(\vec{F}\; \cdotp d \vec{r}\) = 0。 当我们沿着弧线移动时,没有做任何工作。 使用引力的表达式并记下路径两段的\(\vec{F}\; \cdotp d \vec{r}\)值,我们得到
\[ \begin{align} \Delta U &= - \int_{r_{1}}^{r_{2}} \vec{F}\; \cdotp d \vec{r} \\[4pt] &= GM_{E} m \int_{r_{1}}^{r_{2}} \frac{dr}{r^{2}} \\[4pt] &= GM_{E} m \left(\dfrac{1}{r_{1}} - \dfrac{1}{r_{2}}\right) \ldotp \label{eq13.3} \end{align} \]
因为\(\Delta U = U_2 − U_1\)我们可以用一个简单的表达式来表示\(U\):
\[U = - \frac{GM_{E} m}{r} \ldotp \label{13.4}\]
请注意这个定义中的两个重要项目。 首先,\(U → 0\)如\(r → \infty\)。 当两个质量相距无限远时,势能为零。 只有区别才\(U\)是重要的,所以选择 f\(U = 0\) or 只不过\(r = \infty\)是方便而已。 (回想一下,在之前的重力问题中,你可以自由地进入建筑物的顶部或底部,或者任何地方。)\(U = 0\) 其次,请注意,\(U\)随着群众越来越近,这种情况变得越来越消极。 这与你在《势能与节能》中学到的关于潜在能量的知识是一致的。 当两个质量分开时,必须对重力进行正向工作,从而\(U\)增加重力(减少负值)。 所有质量在重力的影响下自然会聚在一起,从较高的势能下降到较低的势能。
将9000公斤的联盟号飞行器从地球表面提升到距离地表400公里的国际空间站的高度需要多少能量?
策略
使用方程\ ref {eq13.3} 找出有效载荷势能的变化。 必须提供足够的功率或能量才能提升有效载荷。
解决方案
注意这样一个事实,即我们从地球表面开始,终点在离地表 400 千米处,变化\(U\)是
我们插入值
- \(m = 9000\; kg\)
- \(M_{E} = 5.96 \times 10^{24}\; kg\)
- \(R_{E} = 6.37 \times 10^{6}\; m\)
然后将 400 千米转换为 4.00 x 10 5 米。我们发现\(\Delta U = 3.32 \times 10^{10} J\)。 正如我们预期的那样,它是积极的,表明潜在能量有所增加。
意义
从角度来看,假设2013年美国家庭的平均能源使用量为每月909千瓦时。 那就是能量
\[909\; kWh \times 1000\; W/kW \times 3600\; s/h = 3.27 \times 10^{9}\; J\; per\; month \ldotp \nonumber\]
因此,我们的结果是能源消耗相当于 10 个月。 但是,这只是将有效载荷提升400公里所需的能量。 如果我们想让联盟号进入轨道以便它能够与国际空间站会合,而不仅仅是掉回地球,它需要大量的动能。 正如我们在下一节中看到的那样,动能大约是\(\Delta\) U的五倍。此外,提升推进系统本身消耗的能量要多得多。 太空旅行并不便宜。
为什么不改用方程\ ref {simple} 中更简单的表达式呢? 错误会有多严重? (距离地球 400 千米\(g\)处的值为 8.67 m/s 2。)
节约能源
在《潜在能量与节能》中,我们描述了如何将能量守恒应用于具有保守力的系统。 我们能够解决许多问题,尤其是那些涉及重力的问题,更简单地说是使用节能。 这些原则和解决问题的策略在这里同样适用。 唯一的改变是将势能的新表达式纳入能量守恒方程中,
\[E_{tot} = K_1 + U_1 = K_2 + U_2.\]
\[\frac{1}{2} mv_{1}^{2} - \frac{GMm}{r_{1}} = \frac{1}{2} mv_{2}^{2} - \frac{GMm}{r_{2}} \label{13.5}\]
请注意,我们使用 M 而不是 M E 来提醒我们,我们不仅限于涉及地球的问题。 但是,我们仍然假设 m << M。(对于不正确的问题,我们需要包括两个质量的动能,并使用动量守恒将速度相互关联起来。 但是原理保持不变。)
逃生速度
逃逸速度通常被定义为物体逃离行星(或月球等任何大型物体)表面并且永不返回所需的最小初始速度。 像往常一样,如果有能量,我们假设大气层不会损失任何能量。
以物体从行星表面发射而其初始速度远离行星的情况为例。 在逃生所需的最小速度下,物体只会在无限远的地方停留,也就是说,物体在达到无穷大时会放弃最后的动能,重力变为零。 由于 U → 0 为 r →\(\infty\),这意味着总能量为零。 因此,通过将总能量设置为零,我们可以找到质量为M和半径为R的天体表面的逃逸速度。 在人体表面,物体位于\(r_1 = R\)并且具有逃生速度\(v_1 = v_{esc}\)。 它\(r_2 = \infty\)以速度到达\(v_2 = 0\)。 代入方程\ ref {13.5},我们有
\[\frac{1}{2} mv_{esc}^{2} - \frac{GMm}{R} = \frac{1}{2} m0^{2} - \frac{GMm}{\infty} = 0 \ldotp\]
求解逃逸速度,
\[v_{esc} = \sqrt{\frac{2GM}{R}} \ldotp \label{13.6}\]
请注意,这\(m\)已经取消了方程式。 无论@@ 质量如何,所有物体的逃逸速度都相同。 此外,我们不仅限于行星表面;R 可以是地球表面以外的任何起点。
从地球表面的逃生速度是多少? 假设空气阻力不会造成能量损失。 将此与从地球轨道开始的逃离太阳的速度进行比较。
策略
我们使用方程式 13.6,明确定义 R 和 M 的值要逃离地球,我们需要地球的质量和半径。 为了逃离太阳,我们需要太阳的质量以及地球和太阳之间的轨道距离。
解决方案
将地球质量和半径的值直接代入方程式13.6,我们得到
\[ \begin {align*} v_{esc} &= \sqrt{\frac{2GM}{R}} \\[4pt] &= \sqrt{\frac{2 (6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(5.96 \times 10^{24}\; kg)}{6.37 \times 10^{6}\; m}} \\[4pt] &= 1.12 \times 10^{4}\; m/s \ldotp \end{align*}\]
这大约是 11 km/s 或 25,000 英里/小时。 为了逃离太阳,从地球轨道开始,我们使用 R = R ES = 1.50 x 10 11 m 和 M Sun = 1.99 x 10 30 kg。 结果是 v esc = 4.21 x 10 4 m/s 或大约 42 km/s。
意义
逃离太阳(离开太阳系)所需的速度几乎是逃离地球表面的速度的四倍。 但是在这两种情况下都有帮助。 地球正在以近1.7 km/s的速度在赤道旋转,我们可以利用这个速度来帮助逃生或进入轨道。 出于这个原因,许多商业航天公司在赤道附近维护发射设施。 为了逃避太阳,还有更多的帮助。 地球以大约 30 km/s 的速度围绕太阳旋转。通过向地球移动的方向发射,我们只需要增加 12 km/s。使用来自其他行星的引力辅助,本质上是一种重力弹弓技术,可以使太空探测器达到更高的速度。 在这种弹弓技术中,飞行器接近地球,并被行星的引力所加速。 它在最近的接近点的速度最快,尽管它的减速幅度与离开的速度相同。 但是相对于地球,飞行器在接近之前和之后很久的速度是相同的。 如果正确选择了方向,则相对于太阳系的其余部分,可能会导致飞行器的速度显著提高(或在需要时降低)。
能量和受引力约束的物体
如前所述,逃逸速度可以定义为可以逃离月球或行星表面的物体的初始速度。 更一般地说,总能量为零的是任何位置的速度。 如果总能量为零或更大,则物体逃脱。 如果总能量为负,则物体无法逃脱。 让我们看看为什么会这样。
如前所述,我们\(U → 0\)将其视为\(r → \infty\)。 如果总能量为零,那么当 m 达到接近无穷大的 r 值时,U 变为零,动能也变为零。 因此,m 在距离 M 无限远的地方休息。它 “刚刚逃脱” 了 M。如果总能量为正,则动能保持不变\(r = \infty\),当然 m 不会返回。 当总能量为零或更大时,我们说 m 没有被引力绑定到 M
另一方面,如果总能量为负,则动能必须在 r 的某个有限值下达到零,其中 U 为负且等于总能量。 物体永远不能超过距离 M 的有限距离,因为这样做需要动能变为负值,这是不可能的。 我们说 m 在引力上与 M 绑定。
我们假设物体是直接离开地球的,从而简化了本次讨论。 值得注意的是,该结果适用于任何速度。 能量是一个标量,因此方程\ ref {13.5} 是一个标量方程——速度的方向在能量守恒中不起作用。 有可能有一个受引力约束的系统,在这种系统中,质量不会 “落在一起”,而是保持彼此的轨道运动。
我们还有一个重要的最后一点看法。 前面我们说过,如果总能量为零或更大,物体就会逃脱。 严格来说,方程\ ref {13.5} 和方程\ ref {13.6} 适用于点对象。 它们也适用于有限大小、球形对称的物体,前提是方程\ ref {13.5}\(r\) 中的值始终大于两个物体的半径之和。 如果 r 小于此总和,则物体发生碰撞。 (即使 r 值更大,但接近半径之和,如果两个物体都是行星大小,引力潮汐力也可能产生显著影响。 我们研究潮汐力中的潮汐效应。) 正总能量和负总能量都不会阻止有限大小的质量发生碰撞。 对于真实物体,方向很重要。
让我们再看前面的例子,在这个例子中,我们计算了从地球轨道开始的逃离地球和太阳的速度。 我们注意到地球的轨道速度已经达到30 km/s。正如我们在下一节中看到的那样,这是保持在环形轨道上所需的切向速度。 如果一个物体在距离地球轨道的距离有这样的速度,但直接远离太阳,那么它在静止之前会行驶多远? 忽略任何其他物体的引力效应。
策略
该物体具有我们可以计算的初始动能和势能。 当它的速度达到零时,它与太阳的距离达到最大值。 我们使用方程式 13.5 即能量守恒来计算动能为零的距离。
解决方案
物体的初始位置是地球的轨道半径,初始速度为 30 km/s。最终速度为零,因此我们可以根据能量守恒方程求解该点的距离。 使用 R ES = 1.50 x 10 11 m 和 M Sun = 1.99 x 10 30 千克,我们有
\[\begin{split} \frac{1}{2} mv_{1}^{2} - \frac{GMm}{r_{1}} & = \frac{1}{2} mv_{2}^{2} - \frac{GMm}{r_{2}} \\ \frac{1}{2} \cancel{m} (30\; km/s)^{2} - \frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(1.99 \times 10^{30}\; kg) \cancel{m}}{1.50 \times 10^{11}\; m} & = \frac{1}{2} m(0)^{2} - \frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(1.99 \times 10^{30}\; kg) \cancel{m}}{r_{2}} \end{split}\]
质量m在哪里取消。 求解 r 2 我们得到 r 2 = 3.0 x 10 11 m。请注意,这是与太阳初始距离的两倍,它带我们越过火星轨道,但不完全到达小行星带。
意义
在这种情况下,物体到达的距离恰好是初始轨道距离的两倍。 我们将在下一节计算圆形轨道的速度时看到其原因。
假设你在地球轨道上绕太阳轨道运行的航天器上,但距离地球很远(因此可以忽略它)。 你怎么能将切线速度重定向到径向方向,这样你就可以通过火星的轨道? 只改变速度方向需要什么?


